Matemáticas | Número total de funciones posibles

En este artículo, estamos discutiendo cómo encontrar el número de funciones de un conjunto a otro. Para comprender los conceptos básicos de las funciones, puede consultar esto: Clases (inyectivas, sobreyectivas, biyectivas) de funciones . 

Número de funciones de un conjunto a otro: Sean X e Y dos conjuntos que tienen m y n elementos respectivamente. En una función de X a Y, cada elemento de X debe asignarse a un elemento de Y. Por lo tanto, cada elemento de X tiene ‘n’ elementos para elegir. Por lo tanto, el número total de funciones será n×n×n.. m veces = n ^m . 
Por ejemplo: X = {a, b, c} e Y = {4, 5}. Una función de X a Y se puede representar en la Figura 1. 
 

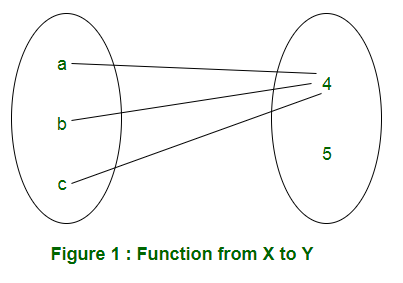
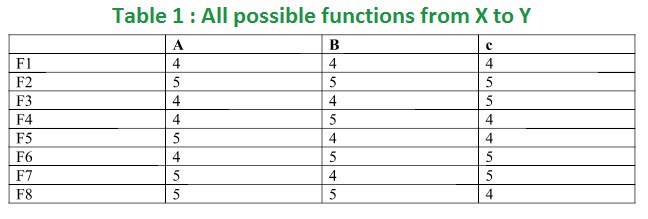
Considerando todas las posibilidades de mapear elementos de X a elementos de Y, el conjunto de funciones se puede representar en la Tabla 1. 

Ejemplos: analicemos las preguntas de puerta basadas en esto: 
 

• Q1. Sean X, Y, Z conjuntos de tamaños x, y y z respectivamente. Sea W = X x Y. Sea E el conjunto de todos los subconjuntos de W. El número de funciones de Z a E es: 
  (A) z ^2xy 
  (B) zx 2 ^xy 
  (C) z ^{2x + y} 
  (D) 2 ^xyz 

  Solución: Como se da W = X x Y, el número de elementos en W es xy. Como E es el conjunto de todos los subconjuntos de W, el número de elementos en E es 2 ^xy . El número de funciones de Z (conjunto de elementos z) a E (conjunto de 2 elementos ^xy ) es 2 ^xyz . Entonces la opción correcta es (D) 
   

• Q2. Sea S el conjunto de todas las funciones f: {0,1} ⁴ → {0,1}. Denote por N el número de funciones de S al conjunto {0,1}. El valor de Log2Log2N es ______. 
  (A) 12 
  (B) 13 
  (C) 15 
  (D) 16 

  Solución: Como se indica en la pregunta, S denota el conjunto de todas las funciones f: {0, 1} ⁴ → {0, 1}. El número de funciones de {0,1} ⁴ (16 elementos) a {0, 1} (2 elementos) son 2 ¹⁶ . Por lo tanto, S tiene 2 ¹⁶ elementos. Además, dado, N denota el número de función de S (2 ¹⁶ elementos) a {0, 1} (2 elementos). Por lo tanto, N tiene 2 ²¹⁶ elementos. Cálculo del valor requerido, 

  Log2(Log2 (2 ²¹⁶ )) =Log2 ¹⁶ = 16 

  Por lo tanto, la opción correcta es (D). 
   

Número de funciones onto de un conjunto a otro: en la función onto de X a Y, se deben usar todos los elementos de Y. En el ejemplo de funciones de X = {a, b, c} a Y = {4, 5}, F1 y F2 que se dan en la Tabla 1 no son sobre. En F1, el elemento 5 del conjunto Y no se usa y el elemento 4 no se usa en la función F2. Entonces, el número total de funciones sobre de X a Y es 6 (F3 a F8). 
 

• Si X tiene m elementos e Y tiene 2 elementos, el número de funciones sobre será 2 ^m -2. 

  Explicación: De un conjunto de m elementos a un conjunto de 2 elementos, el número total de funciones es 2 ^m . De estas funciones, 2 funciones no son sobre (si todos los elementos se asignan al primer ^elemento de Y o todos los elementos se asignan al segundo ^elemento de Y). Entonces, el número de funciones sobre es 2 ^m -2.

• Si X tiene m elementos e Y tiene n elementos, el número de funciones sobre son, 
  
   

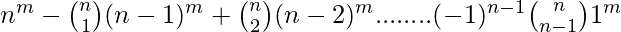
Notas importantes – 
 

• La fórmula funciona solo si m ≥ n.
• Si m < n, el número de funciones sobre es 0 ya que no es posible usar todos los elementos de Y.

Q3. El número de funciones ontológicas (funciones sobreyectivas) del conjunto X = {1, 2, 3, 4} al conjunto Y = {a, b, c} es: (A) 36 (B) 64 (C) 
81 
( 
D 
) 72 

Solución: Usando m = 4 y n = 3, el número de funciones sobre es: 
3 ⁴ – ³ C ₁ (2) ⁴ + ³ C ₂ 1 ⁴ = 36.