Requisito previo: conceptos básicos de combinatoria
Varios problemas de conteo requieren encontrar la cantidad de formas de organizar una cierta cantidad de elementos distintos, donde el orden relativo de estos elementos importa, otros problemas se enfocan en encontrar la cantidad de formas de seleccionar una cantidad particular de elementos de un conjunto, donde el orden de los elementos no importa. Ambos tipos de problemas son similares excepto por una diferencia crucial, esa diferencia es el orden .
permutacion –
Una permutación de un conjunto de objetos distintos es un arreglo ordenado de estos objetos. Una permutación a menudo también se conoce como un arreglo. El orden relativo de los elementos importa en un arreglo.
Una disposición ordenada de los ![]() elementos de un conjunto se denomina permutación r . Se representa como
elementos de un conjunto se denomina permutación r . Se representa como ![]() .
.
para ![]() ,
,
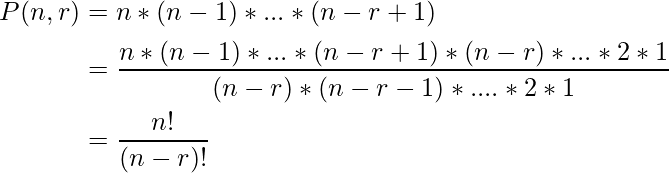
La fórmula anterior para ![]() es una aplicación simple de la regla del producto .
es una aplicación simple de la regla del producto .
- Ejemplo 1: ¿Cuántas permutaciones de la string «ABCDEFGH» tienen la string «ABC» como substring?
- Solución: para que «ABC» sea una substring, las letras A, B y C deben aparecer como un bloque. Si consideramos ese bloque y las 5 letras restantes como objetos, tenemos un total de 6 objetos para ordenar.
Por lo tanto, el número de strings que tienen «ABC» como su substring = 6. = 720.
- Ejemplo 2: encuentre el número de permutaciones de la palabra «CIVILIZACIÓN».
- Solución: la palabra civilización tiene la siguiente frecuencia de caracteres
: ‘C’ – 1
‘I’ – 4
‘V’ – 1
‘L’ – 1
‘Z’ – 1
‘A’ – 1
‘T’ – 1
‘O’ – 1
‘N’ – 1
Si todos los caracteres fueran distintos, el número de permutaciones sería donde
donde  = 12. Pero como la letra ‘I’ se repite 4 veces, el número de permutaciones es menor. Esto se debe a que la permutación como un todo no cambia si los ‘yoes’ están dispuestos entre sí. Entonces, para corregir el número de permutaciones, dividimos el total de permutaciones por
= 12. Pero como la letra ‘I’ se repite 4 veces, el número de permutaciones es menor. Esto se debe a que la permutación como un todo no cambia si los ‘yoes’ están dispuestos entre sí. Entonces, para corregir el número de permutaciones, dividimos el total de permutaciones por  donde
donde 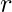 es el número de veces que se repite una letra u objeto.
es el número de veces que se repite una letra u objeto.
Número total de arreglos =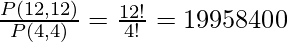
Combinación –
Una combinación de un conjunto de objetos distintos es solo un recuento de la cantidad de formas en que se puede seleccionar una cantidad específica de elementos de un conjunto de cierto tamaño. El orden de los elementos no importa en una combinación.
Una selección desordenada de ![]() elementos de un conjunto se llama combinación r . Se representa como
elementos de un conjunto se llama combinación r . Se representa como ![]() y
y ![]() .
.
Dado que una combinación es solo una permutación sin orden, el número de ![]() combinaciones se puede expresar en términos de
combinaciones se puede expresar en términos de ![]() permutación.
permutación.
La ![]() permutación se puede obtener obteniendo primero la
permutación se puede obtener obteniendo primero la ![]() combinación y luego ordenando los elementos en cada
combinación y luego ordenando los elementos en cada ![]() combinación, lo que se puede hacer de varias
combinación, lo que se puede hacer de varias ![]() maneras.
maneras. ![]()
que nos da-
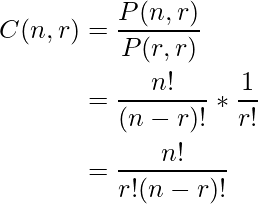
- Ejemplo 1: determine la cantidad de formas en que se pueden elegir 5 cartas de una baraja de 52 cartas, de modo que haya exactamente un as.
- Solución: de los 4 ases, uno puede elegirse de
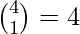 maneras.
maneras.
Las 4 cartas restantes deben elegirse de las 48 cartas restantes. El número de formas de elegir estas 4 cartas es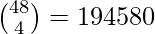 .
.
Número total de formas de elegir 5 cartas por regla de producto =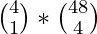 = 4 * 194580 = 778320.
= 4 * 194580 = 778320.
- Ejemplo 2: un polígono tiene 44 diagonales. Halla el número de sus lados.
- Solución: una diagonal es una línea que conecta dos vértices no adyacentes. Si
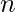 es el número de vértices, entonces el número de pares de vértices no adyacentes =
es el número de vértices, entonces el número de pares de vértices no adyacentes = 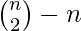 .
. 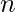 se resta ya que hay
se resta ya que hay 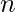 lados.
lados.
Por lo tanto número de diagonales = número de vértices no adyacentes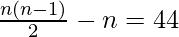
Al resolver obtenemos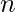 = 11.
= 11.
Coeficientes Binomiales –
Las ![]() combinaciones de un conjunto de
combinaciones de un conjunto de ![]() elementos si se denotan por
elementos si se denotan por ![]() . Este número también se llama coeficiente binomial ya que aparece como un coeficiente en la expansión de potencias de expresiones binomiales.
. Este número también se llama coeficiente binomial ya que aparece como un coeficiente en la expansión de potencias de expresiones binomiales.
El teorema del binomio da una potencia de una expresión binomial como una suma de términos que involucran coeficientes binomiales.
Formalmente,
sean ![]() y
y ![]() sean variables y
sean variables y ![]() sean un entero no negativo. Después
sean un entero no negativo. Después
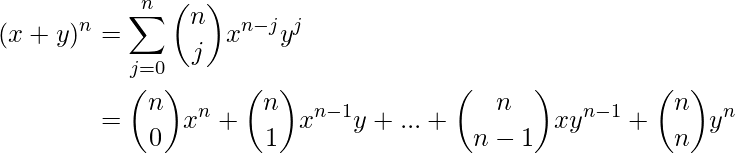
- Ejemplo 1 – ¿Cuál es el coeficiente de
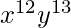 en la expansión de
en la expansión de 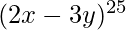 ?
?
- Solución –
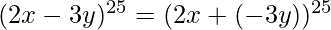 .
.
Por el teorema del binomio-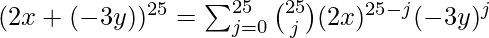
Como la potencia de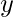 es 13,
es 13, 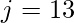 .
.
Por lo tanto el coeficiente de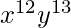 es-
es-
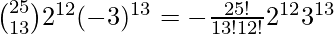
- Ejemplo 2: Demuestre que
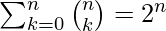 .
.
- Solución – Si ponemos
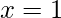 y
y 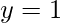 en la expresión del teorema binomial, obtenemos-
en la expresión del teorema binomial, obtenemos-
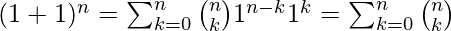
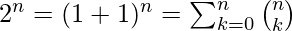
- Ejemplo 3: Demuestre que
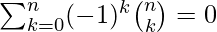 .
.
- Solución – Si ponemos
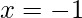 y
y 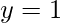 en la expresión del teorema binomial, obtenemos-
en la expresión del teorema binomial, obtenemos-
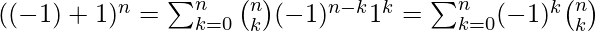
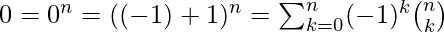
- Ejemplo 4: Demuestre que
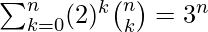 .
.
- Solución – Si ponemos
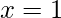 y
y 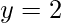 en la expresión del teorema binomial, obtenemos-
en la expresión del teorema binomial, obtenemos-
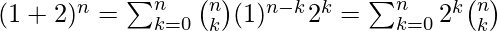
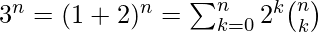
Preguntas de GATE CS Corner
Practicar las siguientes preguntas te ayudará a poner a prueba tus conocimientos. Todas las preguntas se han hecho en GATE en años anteriores o en pruebas simuladas de GATE. Es muy recomendable que los practiques.
Las preguntas 1 y 2 están relacionadas.
1. GATE CS 2007, Pregunta 84
2. GATE CS 2007, Pregunta 85
3. GATE CS 2003, Pregunta 4
4. GATE CS 2003, Pregunta 5
Referencias-
Matemáticas discretas y sus aplicaciones, por Kenneth H Rosen
Este artículo es una contribución de Chirag Manwani . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA