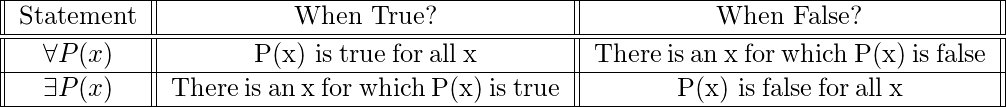Prerrequisito: Introducción a la Lógica Proposicional
Introducción
Considere el siguiente ejemplo. Necesitamos convertir la siguiente oración en una declaración matemática usando solo lógica proposicional.
"Every person who is 18 years or older, is eligible to vote."
La declaración anterior no puede expresarse adecuadamente utilizando solo la lógica proposicional. El problema al tratar de hacerlo es que la lógica proposicional no es lo suficientemente expresiva para tratar con variables cuantificadas. Hubiera sido más fácil si la declaración se refiriera a una persona específica. Pero como no es el caso y la declaración se aplica a todas las personas mayores de 18 años, estamos atascados.
Por lo tanto, necesitamos un tipo de lógica más poderosa.
Lógica de predicados
La lógica de predicados es una extensión de la lógica proposicional. Agrega el concepto de predicados y cuantificadores para capturar mejor el significado de las declaraciones que no pueden expresarse adecuadamente mediante la lógica proposicional.
¿Qué es un predicado?
Considere la declaración, » ![]() es mayor que 3″. Tiene dos partes. La primera parte, la variable
es mayor que 3″. Tiene dos partes. La primera parte, la variable ![]() , es el sujeto del enunciado. La segunda parte, “es mayor que 3”, es el predicado . Se refiere a una propiedad que puede tener el sujeto del enunciado.
, es el sujeto del enunciado. La segunda parte, “es mayor que 3”, es el predicado . Se refiere a una propiedad que puede tener el sujeto del enunciado.
La declaración » ![]() es mayor que 3″ se puede denotar por
es mayor que 3″ se puede denotar por ![]() donde
donde ![]() denota el predicado «es mayor que 3» y
denota el predicado «es mayor que 3» y ![]() es la variable.
es la variable.
El predicado ![]() puede ser considerado como una función. Indica el valor de verdad del enunciado
puede ser considerado como una función. Indica el valor de verdad del enunciado ![]() en
en ![]() . Una vez que se ha asignado un valor a la variable
. Una vez que se ha asignado un valor a la variable ![]() , la declaración
, la declaración ![]() se convierte en una proposición y tiene un valor de verdad o falso (tf).
se convierte en una proposición y tiene un valor de verdad o falso (tf).
En general, una declaración que involucra n variables![]() se puede denotar por
se puede denotar por ![]() . Aquí
. Aquí ![]() también se le conoce como predicado de n-lugar o predicado de n-ario .
también se le conoce como predicado de n-lugar o predicado de n-ario .
- Ejemplo 1: Denotemos
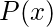 el enunciado “
el enunciado “ 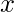 > 10″. ¿ Cuáles son los valores de verdad de
> 10″. ¿ Cuáles son los valores de verdad de 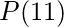 y
y  ?
?
Solución:
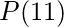 es equivalente al enunciado 11 > 10, que es Verdadero.
es equivalente al enunciado 11 > 10, que es Verdadero.  es equivalente al enunciado 5 > 10, que es Falso.
es equivalente al enunciado 5 > 10, que es Falso. - Ejemplo 2: Denotemos
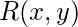 el enunciado “
el enunciado “ 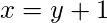 “. ¿ Cuál es el valor de verdad de las proposiciones
“. ¿ Cuál es el valor de verdad de las proposiciones  y
y 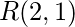 ?
?
Solución: es el enunciado 1 = 3 + 1, que es Falso.
es el enunciado 1 = 3 + 1, que es Falso. 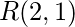 es el enunciado 2 = 1 + 1, que es Verdadero.
es el enunciado 2 = 1 + 1, que es Verdadero.
¿Qué son los cuantificadores?
En la lógica de predicados, los predicados se usan junto con los cuantificadores para expresar hasta qué punto un predicado es verdadero en una variedad de elementos. El uso de cuantificadores para crear tales proposiciones se denomina cuantificación .
Hay dos tipos de cuantificación:
1. Cuantificación universal: las declaraciones matemáticas a veces afirman que una propiedad es verdadera para todos los valores de una variable en un dominio particular, llamado dominio del discurso . Tal declaración se expresa utilizando la cuantificación universal.
La cuantificación universal de ![]() para un dominio particular es la proposición que afirma que
para un dominio particular es la proposición que afirma que ![]() es verdadera para todos los valores de
es verdadera para todos los valores de ![]() en este dominio. El dominio es muy importante aquí ya que decide los posibles valores de
en este dominio. El dominio es muy importante aquí ya que decide los posibles valores de ![]() . El significado de la cuantificación universal de
. El significado de la cuantificación universal de ![]() los cambios cuando se cambia el dominio. El dominio debe especificarse cuando se utiliza una cuantificación universal, ya que sin ella no tiene sentido.
los cambios cuando se cambia el dominio. El dominio debe especificarse cuando se utiliza una cuantificación universal, ya que sin ella no tiene sentido.
Formally, The universal quantification ofis the statement "
for all values of
in the domain" The notation
denotes the universal quantification of
. Here
is called the universal quantifier.
is read as "for all
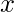
".
- Ejemplo 1: Sea
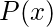 el enunciado “
el enunciado “ 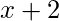 >
> 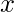 “. ¿ Cuál es el valor de verdad del enunciado
“. ¿ Cuál es el valor de verdad del enunciado 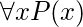 ?
?
Solución: Como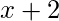 es mayor que
es mayor que 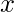 para cualquier número real, entonces
para cualquier número real, entonces 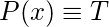 para todo
para todo 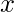 o
o 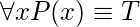 .
.
2. Cuantificación existencial: algunas declaraciones matemáticas afirman que hay un elemento con una determinada propiedad. Tales declaraciones se expresan mediante la cuantificación existencial. La cuantificación existencial se puede usar para formar una proposición que es verdadera si y solo si ![]() es verdadera para al menos un valor de
es verdadera para al menos un valor de ![]() en el dominio.
en el dominio.
Formally, The existential quantification ofis the statement "There exists an element
in the domain such that
" The notation
denotes the existential quantification of
. Here
is called the existential quantifier.
is read as "There is atleast one such
such that
".
- Ejemplo : Sea
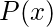 el enunciado “
el enunciado “ 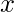 > 5″. ¿ Cuál es el valor de verdad del enunciado
> 5″. ¿ Cuál es el valor de verdad del enunciado 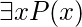 ?
?
Solución: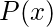 es verdadera para todos los números reales mayores que 5 y falsa para todos los números reales menores que 5. Entonces
es verdadera para todos los números reales mayores que 5 y falsa para todos los números reales menores que 5. Entonces 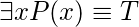 .
.
Resumir,
Ahora, si tratamos de convertir la declaración, dada al principio de este artículo, en una declaración matemática utilizando la lógica de predicados, obtendríamos algo como:
Here, P(x) is the statement "x is 18 years or older and, Q(x) is the statement "x is eligible to vote".
Tenga en cuenta que la declaración dada no se menciona como bicondicional y, sin embargo, usamos uno. Esto se debe a que el lenguaje natural a veces es ambiguo y hemos hecho una suposición. Se hizo esta suposición ya que es cierto que una persona puede votar si y solo si tiene 18 años o más. Consulte Introducción a la lógica proposicional para obtener más explicaciones.
Otros cuantificadores:
aunque los cuantificadores universales y existenciales son los más importantes en Matemáticas e Informática, no son los únicos. De hecho, no hay limitación en el número de cuantificadores diferentes que se pueden definir, como “exactamente dos”, “no hay más de tres”, “hay al menos 10”, etc.
De todos los otros cuantificadores posibles, el que se ve con más frecuencia es el cuantificador de unicidad , denotado por ![]() .
.
The notationstates "There exists a unique
such that
is true".
Cuantificadores con dominios restringidos
Como sabemos, los cuantificadores no tienen sentido si las variables que unen no tienen un dominio. La siguiente notación abreviada se usa para restringir el dominio de las variables- ![]() > 0,
> 0, ![]() > 0.
> 0.
La declaración anterior restringe el dominio de ![]() , y es una forma abreviada de escribir otra proposición, que dice
, y es una forma abreviada de escribir otra proposición, que dice ![]() , en la declaración.
, en la declaración.
Si tratamos de reescribir esta declaración usando una implicación, obtendríamos- ![]() >
> ![]() >
> ![]()
De manera similar, una declaración que usa el cuantificador existencial puede reformularse usando la conjunción entre la proposición que restringe el dominio y el predicado real.
- La restricción de la cuantificación universal es lo mismo que la cuantificación universal de una declaración condicional.
- La restricción de una cuantificación existencial es lo mismo que la cuantificación existencial de la conjunción.
Definiciones a tener en cuenta:
1. Variables vinculantes: una variable cuya ocurrencia está limitada por un cuantificador se denomina
variable vinculada . Las variables que no están limitadas por ningún cuantificador se denominan variables libres .
2. Alcance: la parte de la expresión lógica a la que se aplica un cuantificador se denomina
alcance del cuantificador.
Este tema se ha tratado en dos partes. La segunda parte de este tema se explica en otro artículo – Predicados y cuantificadores – Conjunto 2
Referencias –
Lógica de primer orden –
Cuantificadores de Wikipedia –
Matemáticas discretas de Wikipedia y sus aplicaciones, por Kenneth H Rosen
Este artículo es una contribución de Chirag Manwani . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA