Matemáticas | Representaciones de Arrays y Grafos en Relaciones

Anteriormente, ya hemos discutido las Relaciones y sus tipos básicos.  
Relación combinada: 
Supongamos que R es una relación del conjunto A al B y S es una relación del conjunto B al C, la combinación de ambas relaciones es la relación que consta de pares ordenados (a,c) donde a Є A y c Є C y existe un elemento b Є B para el cual (a,b) Є R y (b,c) Є S. Esto se representa como RoS. 

Relación inversa: 
una relación R se define como (a,b) Є R del conjunto A al conjunto B, luego la relación inversa se define como (b,a) Є R del conjunto B al conjunto A. La relación inversa se representa como R ^-1

R – ¹ = {(b,a) | (a,b) Є R}. 

Relación complementaria: 
Sea R una relación del conjunto A a B, entonces la relación complementaria se define como- {(a,b) } donde (a,b) no es Є R. 

Representación de Relaciones: 
Las relaciones se pueden representar como Arrays y Gráficos dirigidos. 

Relación como Arrays: 
Una relación R se define como del conjunto A al conjunto B, entonces la representación matricial de la relación es M _R = [m _ij ] donde 

m _ij = { 1, si (a,b) Є R 
 

0, si (a,b) Є R } 

Propiedades: 
 

1. Una relación R es reflexiva si los elementos de la diagonal de la array son 1. 
   
    
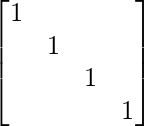
2. Una relación R es irreflexiva si los elementos de la diagonal de la array son 0.
3. Una relación R es simétrica si la transpuesta de la array de relación es igual a su array de relación original. es decir , METRO _R = (METRO _R ) ^T . 
   
    
4. Una relación R es antisimétrica si m _ij = 0 o m _ji =0 cuando i≠j.
5. Una relación sigue la propiedad de unión, es decir, la unión de la array M1 y M2 es M1 V M2, que se representa como R1 U R2 en términos de relación.
6. Una relación sigue la propiedad de encuentro si el encuentro de la array M1 y M2 es M1 ^ M2 que se representa como R1 Λ R2 en términos de relación.

Relaciones como grafos dirigidos: 

Un gráfico dirigido consta de Nodes o vértices conectados por aristas o arcos dirigidos. Sea R una relación del conjunto A al conjunto B definida como (a,b) Є R, luego en el gráfico dirigido se representa como un borde (una flecha de a a b) entre (a,b). 

Propiedades: 
 

1. Una relación R es reflexiva si hay un bucle en cada Node del gráfico dirigido.
2. Una relación R es irreflexiva si no hay bucle en ningún Node de grafos dirigidos.
3. Una relación R es simétrica si para cada arista entre Nodes distintos, siempre hay una arista en dirección opuesta.
4. Una relación R es asimétrica si nunca hay dos aristas en dirección opuesta entre Nodes distintos.
5. Una relación R es transitiva si hay una arista de a a b y de b a c, entonces siempre hay una arista de a a c.

Ejemplo: 

La gráfica dirigida de la relación R = {(a,a),(a,b),(b,b),(b,c),(c,c),(c,b),(c,a)} se representa como: 

Dado que hay un bucle en cada Node, es reflexivo pero no es simétrico ni antisimétrico, ya que hay un borde de a a b pero no hay un borde opuesto de b a a y también un borde dirigido de b a c en ambas direcciones. R no es transitiva ya que hay un borde de a a b y de b a c pero no hay borde de a a c. 

Este artículo es una contribución de Nitika Bansal . 

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente. 

Artículos Relacionados:  
Relaciones y sus tipos