SECUENCIA:
Es un conjunto de números en un orden definido de acuerdo con alguna regla (o reglas) definida.
Cada número del conjunto se llama término de la sucesión y su longitud es el número de términos que contiene. Podemos escribir la secuencia como ![]() . Una sucesión finita generalmente se describe mediante un 1 , un 2 , un 3 …. a n , y una sucesión infinita se describe mediante a 1 , a 2 , a 3 …. hasta el infinito. Una secuencia {a n } tiene el límite L y escribimos
. Una sucesión finita generalmente se describe mediante un 1 , un 2 , un 3 …. a n , y una sucesión infinita se describe mediante a 1 , a 2 , a 3 …. hasta el infinito. Una secuencia {a n } tiene el límite L y escribimos ![]() o
o ![]() como
como ![]() .
.
Por ejemplo:
2, 4, 6, 8 ...., 20 is a finite sequence obtained by adding 2 to the previous number. 10, 6, 2, -2, ..... is an infinite sequence obtained by subtracting 4 from the previous number.
Si los términos de una sucesión se pueden describir mediante una fórmula, entonces la sucesión se llama progresión .
1, 1, 2, 3, 5, 8, 13, ....., is a progression called the Fibonacci sequence in which each term is the sum of the previous two numbers.
Teoremas:
Teorema 1 : dada la sucesión ![]() si tenemos una función f(x) tal que f(n) =
si tenemos una función f(x) tal que f(n) = ![]() y
y ![]() entonces
entonces![]() Este teorema básicamente nos dice que tomamos los límites de las sucesiones de la misma manera que tomamos el límite de las funciones.
Este teorema básicamente nos dice que tomamos los límites de las sucesiones de la misma manera que tomamos el límite de las funciones.
Teorema 2 (Teorema de compresión) : si ![]() para todo n > N para algún N y
para todo n > N para algún N y ![]() luego
luego![]()
Teorema 3 : Si ![]() entonces
entonces ![]() . Tenga en cuenta que para que este teorema se cumpla, el límite DEBE ser cero y no funcionará para una secuencia cuyo límite no sea cero.
. Tenga en cuenta que para que este teorema se cumpla, el límite DEBE ser cero y no funcionará para una secuencia cuyo límite no sea cero.
Teorema 4 : Si ![]() y la función f es continua en L , entonces
y la función f es continua en L , entonces![]()
Teorema 5 : La sucesión ![]() es convergente si
es convergente si ![]() y divergente para
y divergente para
todos los demás valores de r. Además,
este teorema es un teorema útil que da la convergencia/divergencia y el valor (para cuando es convergente) de una secuencia que surge en ocasiones.
Propiedades:
Si ![]() y
y ![]() son sucesiones convergentes, se cumplen las siguientes propiedades:
son sucesiones convergentes, se cumplen las siguientes propiedades:
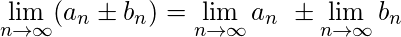
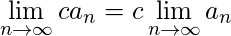
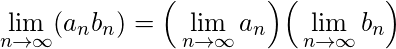
![Rendered by QuickLaTeX.com \displaystyle\lim_{n\to\infty} {a_n}^p = \Big[\displaystyle\lim_{n\to\infty} a_n\Big]^p](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a1c1b3c9f7ec2a1cbd26ceb17ca3a7ec_l3.png) previsto
previsto
Y la última propiedad es
SERIE:
Una serie es simplemente la suma de los diversos términos de una sucesión.
Si la sucesión es ![]() la expresión
la expresión ![]() se llama la serie asociada a ella. Una serie está representada por ‘S’ o el símbolo griego
se llama la serie asociada a ella. Una serie está representada por ‘S’ o el símbolo griego 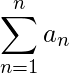 . La serie puede ser finita o infinita.
. La serie puede ser finita o infinita.
Ejemplos:
5 + 2 + (-1) + (-4) is a finite series obtained by subtracting 3 from the previous number. 1 + 1 + 2 + 3 + 5 is an infinite series called the Fibonacci series obtained from the Fibonacci sequence.
Si la sucesión de sumas parciales es una sucesión convergente (es decir, su límite existe y es finito), entonces la serie también se llama convergente, es decir, si ![]() entonces
entonces 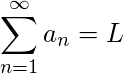 . Asimismo, si la secuencia de sumas parciales es una secuencia divergente (es decir, si
. Asimismo, si la secuencia de sumas parciales es una secuencia divergente (es decir, si ![]() su límite no existe o es más o menos infinito), entonces la serie también se llama divergente.
su límite no existe o es más o menos infinito), entonces la serie también se llama divergente.
Propiedades:
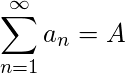 y
y 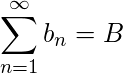 son series convergentes entonces
son series convergentes entonces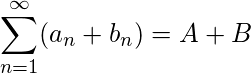
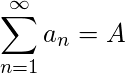 y
y 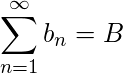 son series convergentes entonces
son series convergentes entonces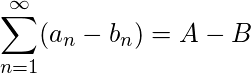
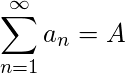 es una serie convergente entonces
es una serie convergente entonces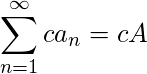
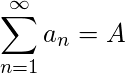 y
y 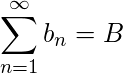 son series convergentes entonces si
son series convergentes entonces si Teoremas:
(1) La convergencia de
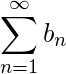 implica la convergencia de
implica la convergencia de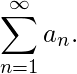
(2) La convergencia de
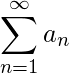 implica la convergencia de
implica la convergencia de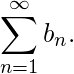
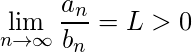 . Entonces
. Entonces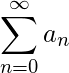 converge si y solo si
converge si y solo si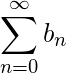 converge.
converge.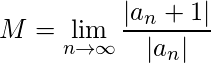 . Entonces,
. Entonces,(1) Si
(2) Si
(3) Si
(1) Si
(2) Si
(3) Si
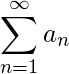 es absolutamente convergente si la serie
es absolutamente convergente si la serie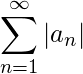 converge.
converge.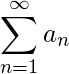 es condicionalmente convergente si la serie
es condicionalmente convergente si la serie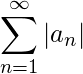 diverge pero la serie
diverge pero la serie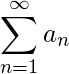 converge.
converge.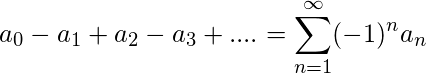 convergerá.
convergerá.RESUMENES:
La suma es la adición de una secuencia de números. Es una forma abreviada conveniente y simple que se usa para dar una expresión concisa para la suma de los valores de una variable.
El símbolo de suma 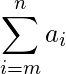 , nos instruye a sumar los elementos de una secuencia. Un elemento típico de la secuencia que se está sumando aparece a la derecha del signo de suma.
, nos instruye a sumar los elementos de una secuencia. Un elemento típico de la secuencia que se está sumando aparece a la derecha del signo de suma.
Propiedades:
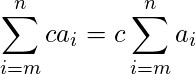 donde c es cualquier número. Entonces, podemos factorizar constantes a partir de una suma.
donde c es cualquier número. Entonces, podemos factorizar constantes a partir de una suma.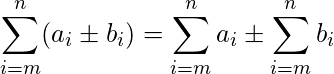 Entonces podemos descomponer una suma en una suma o diferencia.
Entonces podemos descomponer una suma en una suma o diferencia.Tenga en cuenta que si bien podemos dividir sumas y diferencias como se mencionó anteriormente, no podemos hacer lo mismo con productos y cocientes. En otras palabras,

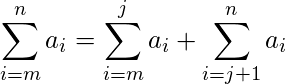 , para cualquier número natural
, para cualquier número natural 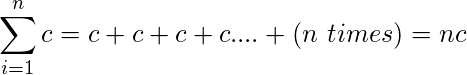 . Si el argumento de la suma es una constante, entonces la suma es el valor del rango límite multiplicado por la constante.
. Si el argumento de la suma es una constante, entonces la suma es el valor del rango límite multiplicado por la constante.Ejemplos:
1) Sum of first n natural numbers:. 2) Sum of squares of first n natural numbers:
. 3) Sum of cubes of first n natural numbers:
. 4) The property of logarithms:
.