Supongamos que f(x) es una función que cumple tres condiciones:
1) f(x) es continua en el intervalo cerrado a ≤ x ≤ b
2) f(x) es diferenciable en el intervalo abierto a < x < b
3) f(a) = f(b)
Entonces, de acuerdo con el Teorema de Rolle, existe al menos un punto ‘c’ en el intervalo abierto (a, b) tal que:
f'(c) = 0
Podemos visualizar el teorema de Rolle de la figura (1)
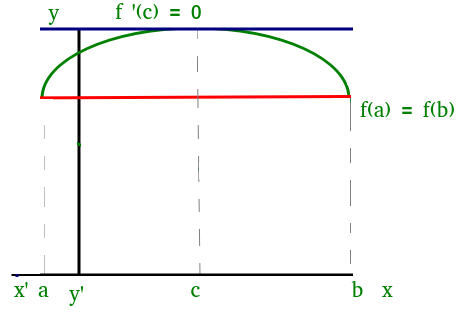
Figure(1)
En la figura anterior, la función satisface las tres condiciones dadas anteriormente. Entonces, podemos aplicar el teorema de Rolle, según el cual existe al menos un punto ‘c’ tal que:
f'(c) = 0
lo que significa que existe un punto en el que la pendiente de la tangente en eso es igual a 0. Podemos ver fácilmente que en el punto ‘c’ la pendiente es 0.
De manera similar, podría haber más de un punto en el que la pendiente de la tangente en esos puntos serán 0. La figura (2) es uno de los ejemplos donde existe más de un punto que satisface el teorema de Rolle.
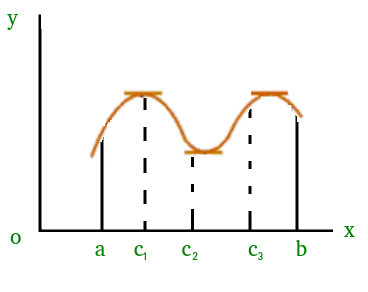
Figura 2)
Este artículo ha sido contribuido por Saurabh Sharma.
Si desea contribuir, envíenos un correo electrónico con su interés a contribuir@geeksforgeeks.org
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA