Maximice el recuento de cuadrados únicos que se pueden formar con N puntos arbitrarios en el plano de coordenadas

Dado un entero positivo N , la tarea es encontrar el número máximo de cuadrados únicos que se pueden formar con N puntos arbitrarios en el plano de coordenadas.

Nota: Cualquier par de cuadrados que no se superpongan se consideran únicos.

Ejemplos:

Entrada: N = 9
Salida: 5
Explicación:
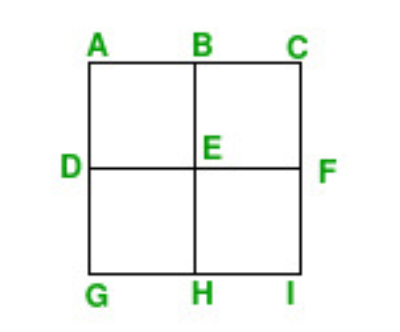
Considere el siguiente cuadrado que consta de N puntos:

Los cuadrados ABEF, BCFE, DEHG, EFIH son uno de los posibles cuadrados de tamaño 1 que no se superponen entre sí.
El cuadrado ACIG es también uno de los posibles cuadrados de tamaño 2.

Entrada: N = 6
Salida: 2

Enfoque: Este problema se puede resolver en base a las siguientes observaciones:

Observe que si N es un cuadrado perfecto, entonces el número máximo de cuadrados se formará cuando los puntos sqrt(N)*sqrt(N) forman una cuadrícula de sqrt(N)*sqrt(N) y todos ellos son espacios iguales.
Pero cuando N no es un cuadrado perfecto , todavía forma una cuadrícula pero con el mayor número que es un cuadrado perfecto que tiene un valor menor que N.
Las coordenadas restantes se pueden colocar alrededor de los bordes de la cuadrícula, lo que conducirá al máximo de cuadrados posibles.

Siga los pasos a continuación para resolver el problema:

Inicialice una variable, digamos ans , que almacene el recuento resultante de cuadrados formados.
Encuentre el tamaño de cuadrícula máximo posible como sqrt (N) y el recuento de todos los cuadrados posibles formados hasta la longitud len a la variable ans que se puede calcular mediante $\sum_{i = 1}^{i = len} i*i$ .
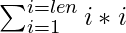Disminuye el valor de N por len*len .
Si el valor de N es al menos len , todos los demás cuadrados se pueden formar colocándolos en otro grupo de puntos. Encuentre el conteo de cuadrados calculado en el Paso 2 para el valor de len .
Después de completar los pasos anteriores, imprima el valor de ans como resultado.

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the maximum number
// of unique squares that can be formed
// from the given N points
int maximumUniqueSquares(int N)
{
    // Stores the resultant count of
    // squares formed
    int ans = 0;
 
    // Base Case
    if (N < 4) {
        return 0;
    }
 
    // Subtract the maximum possible
    // grid size as sqrt(N)
    int len = (sqrt(double(N)));
    N -= len * len;
 
    // Find the total squares till now
    // for the maximum grid
    for (int i = 1; i < len; i++) {
 
        // A i*i grid contains (i-1)*(i-1)
        // + (i-2)*(i-2) + ... + 1*1 squares
        ans += i * i;
    }
 
    // When N >= len then more squares
    // will be counted
    if (N >= len) {
        N -= len;
        for (int i = 1; i < len; i++) {
            ans += i;
        }
    }
 
    for (int i = 1; i < N; i++) {
        ans += i;
    }
 
    // Return total count of squares
    return ans;
}
 
// Driver Code
int main()
{
    int N = 9;
    cout << maximumUniqueSquares(N);
 
    return 0;
}

Java

// Java program for the above approach
import java.io.*;
 
class GFG {
 
// Function to find the maximum number
// of unique squares that can be formed
// from the given N points
static int maximumUniqueSquares(int N)
{
    // Stores the resultant count of
    // squares formed
    int ans = 0;
 
    // Base Case
    if (N < 4) {
        return 0;
    }
 
    // Subtract the maximum possible
    // grid size as sqrt(N)
    int len = (int)(Math.sqrt(N));
    N -= len * len;
 
    // Find the total squares till now
    // for the maximum grid
    for (int i = 1; i < len; i++) {
 
        // A i*i grid contains (i-1)*(i-1)
        // + (i-2)*(i-2) + ... + 1*1 squares
        ans += i * i;
    }
 
    // When N >= len then more squares
    // will be counted
    if (N >= len) {
        N -= len;
        for (int i = 1; i < len; i++) {
            ans += i;
        }
    }
 
    for (int i = 1; i < N; i++) {
        ans += i;
    }
 
    // Return total count of squares
    return ans;
}
 
// Driver Code
public static void main (String[] args)
{
    int N = 9;
    System.out.println( maximumUniqueSquares(N));
 
}
}
 
// This code is contributed by shivanisinghss2110.

Python3

# Python program for the above approach
 
# for math function
import math
 
# Function to find the maximum number
# of unique squares that can be formed
# from the given N points
def maximumUniqueSquares(N):
   
    # Stores the resultant count of
    # squares formed
    ans = 0
     
    # Base Case
    if N < 4:
        return 0
 
    # Subtract the maximum possible
    # grid size as sqrt(N)
    len = int(math.sqrt(N))
 
    N -= len * len
 
    # Find the total squares till now
    # for the maximum grid
    for i in range(1, len):
 
        # A i*i grid contains (i-1)*(i-1)
        # + (i-2)*(i-2) + ... + 1*1 squares
        ans += i * i
 
    # When N >= len then more squares
    # will be counted
    if (N >= len):
        N -= len
        for i in range(1, len):
            ans += i
 
    for i in range(1, N):
        ans += i
 
    # Return total count of squares
    return ans
 
# Driver Code
if __name__ == "__main__":
    N = 9
    print(maximumUniqueSquares(N))
     
    # This code is contributed by rakeshsahni

C#

// C# program for the above approach
using System;
 
public class GFG
{
 
    // Function to find the maximum number
    // of unique squares that can be formed
    // from the given N points
    static int maximumUniqueSquares(int N)
    {
       
        // Stores the resultant count of
        // squares formed
        int ans = 0;
     
        // Base Case
        if (N < 4) {
            return 0;
        }
     
        // Subtract the maximum possible
        // grid size as sqrt(N)
        int len = (int)(Math.Sqrt(N));
        N -= len * len;
     
        // Find the total squares till now
        // for the maximum grid
        for (int i = 1; i < len; i++) {
     
            // A i*i grid contains (i-1)*(i-1)
            // + (i-2)*(i-2) + ... + 1*1 squares
            ans += i * i;
        }
     
        // When N >= len then more squares
        // will be counted
        if (N >= len) {
            N -= len;
            for (int i = 1; i < len; i++) {
                ans += i;
            }
        }
     
        for (int i = 1; i < N; i++) {
            ans += i;
        }
     
        // Return total count of squares
        return ans;
    }
     
    // Driver Code
    public static void Main (string[] args)
    {
        int N = 9;
        Console.WriteLine( maximumUniqueSquares(N));
     
    }
}
 
// This code is contributed by AnkThon

Javascript

<script>
 
 
// Javascript program for the above approach
 
// Function to find the maximum number
// of unique squares that can be formed
// from the given N points
function maximumUniqueSquares(N)
{
    // Stores the resultant count of
    // squares formed
    var ans = 0;
    var i;
 
    // Base Case
    if (N < 4) {
        return 0;
    }
 
    // Subtract the maximum possible
    // grid size as sqrt(N)
    var len = Math.sqrt(N);
    N -= len * len;
 
    // Find the total squares till now
    // for the maximum grid
    for (i = 1; i < len; i++) {
 
        // A i*i grid contains (i-1)*(i-1)
        // + (i-2)*(i-2) + ... + 1*1 squares
        ans += i * i;
    }
 
    // When N >= len then more squares
    // will be counted
    if (N >= len) {
        N -= len;
        for (i = 1; i < len; i++) {
            ans += i;
        }
    }
 
    for (i = 1; i < N; i++) {
        ans += i;
    }
 
    // Return total count of squares
    return ans;
}
 
// Driver Code
    var N = 9;
    document.write(maximumUniqueSquares(N));
 
// This code is contributed by SURENDRA_GANGWAR.
</script>

Producción:

Complejidad de tiempo: O(sqrt(N))
Espacio auxiliar: O(1)

Publicación traducida automáticamente

Artículo escrito por kartikmodi y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta