Dado un gráfico no dirigido de N Nodes y M vértices. También se le da un borde K como seleccionado[] . La tarea de maximizar la longitud de la ruta más corta entre el Node 1 y el Node N agregando aristas individuales entre dos vértices cualesquiera de las aristas seleccionadas dadas.
Nota: Puede agregar una arista entre dos vértices seleccionados que ya tengan una arista entre ellos.
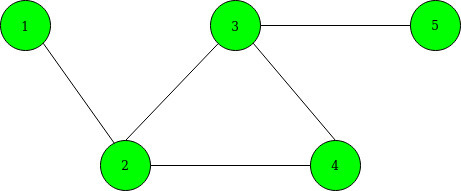
Entrada: N = 5, M = 4, K = 2, seleccionado[] = {2, 4}
A continuación se muestra el gráfico dado:
Salida: 3
Explicación:
antes de agregar un borde entre 2 y 4, la ruta más corta se convierte en: 1–>2–>3–>4–>5.
Después de agregar un borde entre 2 y 4, la ruta más corta se convierte en 1–>2–>4–>5. A continuación se muestra el gráfico después de agregar bordes. indicado por la línea discontinua.
Entrada: N = 5 M = 5 K = 3 seleccionados[] = {1, 3, 5}
A continuación se muestra el gráfico dado:
Salida: 3
Explicación:
Podemos agregar una arista entre 3 y 5 ya que ya tienen una arista entre ellos. entonces, el camino más corto se convierte en 1–>2–>3–>5. A continuación se muestra el gráfico después de agregar bordes. indicado por la línea discontinua.
Enfoque: la idea es utilizar la búsqueda primero en amplitud para encontrar la distancia desde los vértices 1 y N hasta cada vértice seleccionado. Para el vértice i seleccionado, sea x i la distancia al Node 1 e y i la distancia al Node N . A continuación se muestran los pasos:
- Mantenga una array 2D (digamos dist[2][] ) que tenga 2 filas y N columnas.
- En la primera fila, mantenga la distancia más corta entre el Node 1 y otros vértices en el gráfico utilizando BFS transversal.
- En la segunda fila, mantenga la distancia más corta entre el Node N y los otros vértices del gráfico utilizando BFS transversal.
- Ahora, elige dos vértices seleccionados a y b de selected[] para minimizar el valor de min(xa + yb, ya + xb). Para esto haz lo siguiente:
- Cree un vector de pares y almacene el valor de (x i – y i ) con su respectivo Node seleccionado.
- Ordene el vector de pares anterior .
- Inicialice best a 0 y max a -INF .
- Ahora recorra el vector de pares anterior y para cada Node seleccionado (digamos a) actualice el valor de mejor al máximo de (mejor, máx + dist[1][a]) y actualice el máximo al máximo de (máx, dist[0] [a]).
- Después de las operaciones anteriores, el máximo de (dist[0][N-1] y mejor + 1) dado el camino mínimo más corto.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
const int INF = 1e9 + 7;
int N, M;
// To store graph as adjacency list
vector<int> edges[200005];
// To store the shortest path
int dist[2][200000];
// Function that performs BFS Traversal
void bfs(int* dist, int s)
{
int q[200000];
// Fill initially each distance as INF
fill(dist, dist + N, INF);
int qh = 0, qt = 0;
q[qh++] = s;
dist[s] = 0;
// Perform BFS
while (qt < qh) {
int x = q[qt++];
// Traverse the current edges
for (int y : edges[x]) {
if (dist[y] == INF) {
// Update the distance
dist[y] = dist[x] + 1;
// Insert in queue
q[qh++] = y;
}
}
}
}
// Function that maximizes the shortest
// path between source and destination
// vertex by adding a single edge between
// given selected nodes
void shortestPathCost(int selected[], int K)
{
vector<pair<int, int> > data;
// To update the shortest distance
// between node 1 to other vertices
bfs(dist[0], 0);
// To update the shortest distance
// between node N to other vertices
bfs(dist[1], N - 1);
for (int i = 0; i < K; i++) {
// Store the values x[i] - y[i]
data.emplace_back(dist[0][selected[i]]
- dist[1][selected[i]],
selected[i]);
}
// Sort all the vectors of pairs
sort(data.begin(), data.end());
int best = 0;
int MAX = -INF;
// Traverse data[]
for (auto it : data) {
int a = it.second;
best = max(best,
MAX + dist[1][a]);
// Maximize x[a] - y[b]
MAX= max(MAX, dist[0][a]);
}
// Print minimum cost
printf("%d\n", min(dist[0][N - 1], best + 1));
}
// Driver Code
int main()
{
// Given nodes and edges
N = 5, M = 4;
int K = 2;
int selected[] = { 1, 3 };
// Sort the selected nodes
sort(selected, selected + K);
// Given edges
edges[0].push_back(1);
edges[1].push_back(0);
edges[1].push_back(2);
edges[2].push_back(1);
edges[2].push_back(3);
edges[3].push_back(2);
edges[3].push_back(4);
edges[4].push_back(3);
// Function Call
shortestPathCost(selected, K);
return 0;
}
Java
// Java program for the above approach
import java.util.*;
import java.lang.*;
class GFG{
static int INF = (int)1e9 + 7;
static int N, M;
// To store graph as adjacency list
static ArrayList<ArrayList<Integer>> edges;
// To store the shortest path
static int[][] dist = new int[2][200000];
// Function that performs BFS Traversal
static void bfs(int[] dist, int s)
{
int[] q = new int[200000];
// Fill initially each distance as INF
Arrays.fill(dist, INF);
int qh = 0, qt = 0;
q[qh++] = s;
dist[s] = 0;
// Perform BFS
while (qt < qh)
{
int x = q[qt++];
// Traverse the current edges
for(Integer y : edges.get(x))
{
if (dist[y] == INF)
{
// Update the distance
dist[y] = dist[x] + 1;
// Insert in queue
q[qh++] = y;
}
}
}
}
// Function that maximizes the shortest
// path between source and destination
// vertex by adding a single edge between
// given selected nodes
static void shortestPathCost(int selected[], int K)
{
ArrayList<int[]> data = new ArrayList<>();
// To update the shortest distance
// between node 1 to other vertices
bfs(dist[0], 0);
// To update the shortest distance
// between node N to other vertices
bfs(dist[1], N - 1);
for(int i = 0; i < K; i++)
{
// Store the values x[i] - y[i]
data.add(new int[]{dist[0][selected[i]] -
dist[1][selected[i]],
selected[i]});
}
// Sort all the vectors of pairs
Collections.sort(data, (a, b) -> a[0] - b[0]);
int best = 0;
int MAX = -INF;
// Traverse data[]
for(int[] it : data)
{
int a = it[1];
best = Math.max(best,
MAX + dist[1][a]);
// Maximize x[a] - y[b]
MAX = Math.max(MAX, dist[0][a]);
}
// Print minimum cost
System.out.println(Math.min(dist[0][N - 1],
best + 1));
}
// Driver code
public static void main (String[] args)
{
// Given nodes and edges
N = 5; M = 4;
int K = 2;
int selected[] = { 1, 3 };
// Sort the selected nodes
Arrays.sort(selected);
edges = new ArrayList<>();
for(int i = 0; i < 200005; i++)
edges.add(new ArrayList<Integer>());
// Given edges
edges.get(0).add(1);
edges.get(1).add(0);
edges.get(1).add(2);
edges.get(2).add(1);
edges.get(2).add(3);
edges.get(3).add(2);
edges.get(3).add(4);
edges.get(4).add(3);
// Function Call
shortestPathCost(selected, K);
}
}
// This code is contributed by offbeat
Python3
# Python3 program for the above approach # Function that performs BFS Traversal def bfs(x, s): global edges, dist q = [0 for i in range(200000)] # Fill initially each distance as INF # fill(dist, dist + N, INF) qh, qt = 0, 0 q[qh] = s qh += 1 dist[x][s] = 0 # Perform BFS while (qt < qh): xx = q[qt] qt += 1 # Traverse the current edges for y in edges[xx]: if (dist[x][y] == 10**18): # Update the distance dist[x][y] = dist[x][xx] + 1 # Insert in queue q[qh] = y qh += 1 # Function that maximizes the shortest # path between source and destination # vertex by adding a single edge between # given selected nodes def shortestPathCost(selected, K): global dist, edges data = [] # To update the shortest distance # between node 1 to other vertices bfs(0, 0) # To update the shortest distance # between node N to other vertices bfs(1, N - 1) for i in range(K): # Store the values x[i] - y[i] data.append([dist[0][selected[i]]- dist[1][selected[i]], selected[i]]) # Sort all the vectors of pairs data = sorted(data) best = 0 MAX = -10**18 # Traverse data[] for it in data: a = it[1] best = max(best,MAX + dist[1][a]) # Maximize x[a] - y[b] MAX= max(MAX, dist[0][a]) # Print minimum cost print(min(dist[0][N - 1], best + 1)) # Driver Code if __name__ == '__main__': # Given nodes and edges edges = [[] for i in range(5)] dist = [[10**18 for i in range(1000005)] for i in range(2)] N,M = 5, 4 K = 2 selected = [1, 3] # Sort the selected nodes selected = sorted(selected) # Given edges edges[0].append(1) edges[1].append(0) edges[1].append(2) edges[2].append(1) edges[2].append(3) edges[3].append(2) edges[3].append(4) edges[4].append(3) # Function Call shortestPathCost(selected, K) # This code is contributed by mohit kumar 29
Javascript
<script>
// Javascript program for the above approach
let INF = 1e9 + 7;
let N, M;
// To store graph as adjacency list
let edges=[];
// To store the shortest path
let dist=new Array(2);
for(let i=0;i<2;i++)
{
dist[i]=new Array(200000);
for(let j=0;j<200000;j++)
{
dist[i][j]=INF;
}
}
// Function that performs BFS Traversal
function bfs(dist,s)
{
let q = new Array(200000);
// Fill initially each distance as INF
let qh = 0, qt = 0;
q[qh++] = s;
dist[s] = 0;
// Perform BFS
while (qt < qh)
{
let x = q[qt++];
// Traverse the current edges
for(let y=0;y< edges[x].length;y++)
{
if (dist[edges[x][y]] == INF)
{
// Update the distance
dist[edges[x][y]] = dist[x] + 1;
// Insert in queue
q[qh++] = edges[x][y];
}
}
}
}
// Function that maximizes the shortest
// path between source and destination
// vertex by adding a single edge between
// given selected nodes
function shortestPathCost(selected,K)
{
let data = [];
// To update the shortest distance
// between node 1 to other vertices
bfs(dist[0], 0);
// To update the shortest distance
// between node N to other vertices
bfs(dist[1], N - 1);
for(let i = 0; i < K; i++)
{
// Store the values x[i] - y[i]
data.push([dist[0][selected[i]] -
dist[1][selected[i]],
selected[i]]);
}
// Sort all the vectors of pairs
data.sort(function(a, b){return a[0] - b[0];});
let best = 0;
let MAX = -INF;
// Traverse data[]
for(let it=0;it< data.length;it++)
{
let a = data[it][1];
best = Math.max(best,
MAX + dist[1][a]);
// Maximize x[a] - y[b]
MAX = Math.max(MAX, dist[0][a]);
}
// Print minimum cost
document.write(Math.min(dist[0][N - 1],
best + 1));
}
// Driver code
// Given nodes and edges
N = 5; M = 4;
let K = 2;
let selected = [ 1, 3 ];
// Sort the selected nodes
(selected).sort(function(a,b){return a-b;});
edges = [];
for(let i = 0; i < 200005; i++)
edges.push([]);
// Given edges
edges[0].push(1);
edges[1].push(0);
edges[1].push(2);
edges[2].push(1);
edges[2].push(3);
edges[3].push(2);
edges[3].push(4);
edges[4].push(3);
// Function Call
shortestPathCost(selected, K);
// This code is contributed by patel2127
</script>
3
Complejidad de tiempo: O(N*log N + M)
Espacio auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por sharadgoyal y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA