Maximizar el número de segmentos de longitud p, q y r

Dada una barra de longitud L, la tarea es cortar la barra de tal manera que se maximice el número total de segmentos de longitud p, q y r. Los segmentos solo pueden tener una longitud p, q y r. 

Ejemplos: 

Entrada: l = 11, p = 2, q = 3, r = 5 
Salida: 5 
Segmentos de 2, 2, 2, 2 y 3

Entrada: l = 7, p = 2, q = 5, r = 5 
Salida: 2 
Segmentos de 2 y 5

Enfoque 1:

Esto se puede visualizar como un problema de recursión clásico, que se reduce aún más al método de memorización (de arriba hacia abajo) de la programación dinámica . Inicialmente, tenemos la longitud l presente con nosotros, tendríamos tres opciones de tamaño para cortar de esto, podemos hacer un corte de longitud p , o q , o r . Digamos que hicimos un corte de longitud p , por lo que la longitud restante sería lp y de manera similar con los cortes q y r resultando en longitudes restantes lq y lrrespectivamente. Llamaremos a la función recursiva para las longitudes restantes y en cualquier instancia posterior tendremos estas tres opciones. Guardaremos la respuesta de todas estas llamadas recursivas y sacaremos el máximo de ellas +1, ya que en cualquier caso también tendremos 1 corte de esta llamada en particular. Además, tenga en cuenta que la llamada recursiva se realizaría si y solo si la longitud disponible es mayor que la longitud que queremos cortar, es decir, suponga que p = 3 , y después de ciertas llamadas recursivas, la longitud disponible es solo 2, por lo que no podemos cortar esto línea en longitudes de p nunca más.

A continuación se muestra el pseudocódigo para el mismo:

if(l==0)  // Base Case
  return 0;
  
  
int a,b,c;
if(p<=l)
   a=func(l-p,p,q,r);
if(q<=l)
   b=func(l-q,p,q,r);
if(r<=l)
   c=func(l-r,p,q,r);
return 1+max({a,b,c});

A continuación se muestra el árbol de recurrencia para l=4,p=2,q=1 y r=1 :

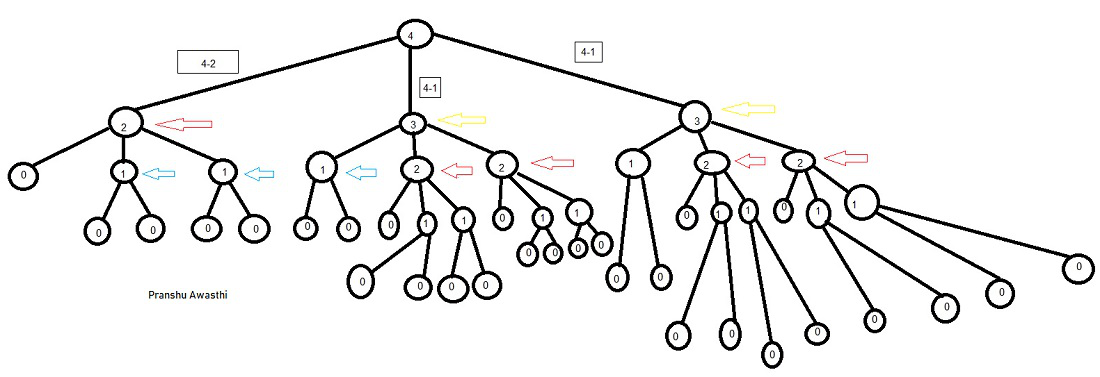
Árbol de recurrencia para l=4, p=2, q=1 y r=1

Se puede observar claramente que en cada llamada, la longitud dada (4 inicialmente) se divide en 3 subpartes diferentes. Además, podemos ver que la recursividad se repite para ciertas entradas ( la flecha roja representa una llamada repetitiva para l=2, amarilla para l=3 y azul para l=1). Por lo tanto, podemos memorizar los resultados en cualquier contenedor o array, de modo que se evite la repetición de las mismas llamadas recursivas.

Ahora, el pseudocódigo anterior cambia a:

vector<int> dp(10005,-1);         // Initialise DP Table ( Array can also be used )


if(l==0)                         // Base Case
 return 0;
 
if(dp[l]!=-1)                 // If already memoized , return from here only
   return dp[l];
int a,b,c;
if(p<=l)
  a=func(l-p,p,q,r);
if(q<=l)
  b=func(l-q,p,q,r);
if(r<=l)
  c=func(l-r,p,q,r);
  
  
return dp[l]=1+max({a,b,c});          // Memoize the result in the dp table & return

Sigamos ahora el código para la implementación del código anterior:

//C++ Code to find maximum number of cut segments
// Memoization DP
 
#include <bits/stdc++.h>
using namespace std;
 
//Function to find the maximum number of cuts.
int dp[10005];
     
int func(int l, int p, int q, int r)
{
    if(l==0)
       return 0;                               // Base Case
            
     if(dp[l]!=-1)                              // If already memoized
        return dp[l];
         
     int a(INT_MIN),b(INT_MIN),c(INT_MIN);         // Intitialise a,b,& c with INT_MIN
   
     if(p<=l)                                      // If Possible to make a cut of length p
        a=func(l-p,p,q,r);
   
     if(q<=l)                                      // If possible to make a cut of length q
        b=func(l-q,p,q,r);
   
     if(r<=l)                                      // If possible to make a cut of length r
        c=func(l-r,p,q,r);
   
     return dp[l]=1+max({a,b,c});                    // Memoize & return
         
}
     
int maximizeTheCuts(int l, int p, int q, int r)
{
    memset(dp,-1,sizeof(dp));                 // Set Lookup table to -1
    int ans=func(l,p,q,r);                    // Utility function call
         
    if(ans<0)
       return 0;                        // If returned answer is negative , that means cuts are not possible
    return ans;
 }
 
int main()
{
 
  int l,p,q,r;
  cout<<"ENTER THE LENGTH OF THE ROD "<<endl;
  cin>>l;
   
  cout<<"ENTER THE VALUES OF p,q & r "<<endl;
  cin>>p>>q>>r;
   
  cout<<"THE MAXIMUM NUMBER OF SEGMENTS THAT CAN BE CUT OF LENGTH p,q & r FROM A ROD OF LENGTH l are "<<maximizeTheCuts(l,p,q,r)<<endl;
    return 0;
}

Complejidad de tiempo : O(n) donde n es la longitud de la barra o segmento de línea que debe cortarse.

Complejidad espacial : O(n) donde n es la longitud de la barra o segmento de línea que debe cortarse.

Enfoque 2: 

Como la solución para un número máximo de cortes que se pueden realizar en una longitud dada depende de la cantidad máxima de cortes realizados previamente en longitudes más cortas, esta pregunta podría resolverse mediante el enfoque de Programación Dinámica. Supongamos que nos dan una longitud ‘l’ . Para encontrar el número máximo de cortes que se pueden hacer en la longitud ‘l’ , encuentre el número de cortes hechos en las longitudes anteriores más cortas ‘l-p’, ‘l-q’, ‘l-r’ respectivamente. La respuesta requerida sería max(lp,lq,lr)+1 ya que se necesitaría un corte más después de esto para cortar la longitud ‘l’ . Entonces, para resolver este problema para una longitud dada, encuentre el número máximo de cortes que se pueden hacer en longitudes que van desde ‘1’ a ‘l’. 

Ejemplo:  

l = 11, p = 2, q = 3, r = 5 
Analizando longitudes de 1 a 11: 

1. No es posible cortar->0
2. El corte posible es de longitudes 2->1 (2)
3. El corte posible es de longitudes 3->1 (3)
4. Los posibles cortes son de longitud max(arr[4-2],arr[4-3])+1->2 (2,2)
5. Los posibles cortes son de longitud max(arr[5-2],arr[5-3])+1->2 (2,3)
6. Los cortes posibles son de longitudes max(arr[6-2],arr[6-3],arr[6-5])+1->3 (2,2,2)
7. Los cortes posibles son de longitudes máximas (arr[7-2],arr[7-3],arr[7-5])+1->3 (2,3,2) o (2,2,3)
8. Los cortes posibles son de longitudes max(arr[8-2],arr[8-3],arr[8-5])+1->4 (2,2,2,2)
9. Los cortes posibles son de longitudes máximas (arr[9-2],arr[9-3],arr[9-5])+1->4 (2,3,2,2) o (2,2,3, 2) o (2,2,2,3)
10. Los cortes posibles son de longitudes máximas (arr[10-2],arr[10-3],arr[10-5])+1->5 (2,2,2,2,2)
11. Los posibles cortes son de longitud máx(arr[11-2],arr[11-3],arr[11-5])+1->5 (2,3,2,2,2) o (2,2, 3,2,2) o (2,2,2,3,2) o (2,2,2,2,3)

Algoritmo: 

1. Inicialice una array DP[]={-1} y DP[0]=0 .
2. Ejecutar un ciclo de ‘1’ a ‘l’
3. Si DP[i]=-1 significa que no es posible dividirlo dando segmentos p,q,r así que continúa;
4. DP[i+p]=máx(DP[i+p],DP[i]+1)
5. DP[i+q]=máx(DP[i+q],DP[i]+1)
6. DP[i+r]=máx(DP[i+r],DP[i]+1)
7. imprimir DP[l]

Pseudocódigo: 

DP[l+1]={-1}
DP[0]=0
for(i from 0 to l)
  if(DP[i]==-1)
  continue
  DP[i+p]=max(DP[i+p],DP[i]+1)
  DP[i+q]=max(DP[i+q],DP[i]+1)
  DP[i+r]=max(DP[i+r],DP[i]+1)

print(DP[l])

Implementación: 

// C++ program to maximize the number
// of segments of length p, q and r
#include <bits/stdc++.h>
using namespace std;
 
// Function that returns the maximum number
// of segments possible
int findMaximum(int l, int p, int q, int r)
{
 
    // Array to store the cut at each length
    int dp[l + 1];
 
    // All values with -1
    memset(dp, -1, sizeof(dp));
 
    // if length of rod is 0 then total cuts will be 0
    // so, initialize the dp[0] with 0
    dp[0] = 0;
 
    for (int i = 0; i <= l; i++) {
 
        // if certain length is not possible
        if (dp[i] == -1)
            continue;
 
        // if a segment of p is possible
        if (i + p <= l)
            dp[i + p] = max(dp[i + p], dp[i] + 1);
 
        // if a segment of q is possible
        if (i + q <= l)
            dp[i + q] = max(dp[i + q], dp[i] + 1);
 
        // if a segment of r is possible
        if (i + r <= l)
            dp[i + r] = max(dp[i + r], dp[i] + 1);
    }
    // if no segment can be cut then return 0
    if (dp[l] == -1) {
        dp[l] = 0;
    }
    // return value corresponding to length l
    return dp[l];
}
 
// Driver Code
int main()
{
    int l = 11, p = 2, q = 3, r = 5;
 
    // Calling Function
    int ans = findMaximum(l, p, q, r);
    cout << ans;
 
    return 0;
}

// Java program to maximize
// the number of segments
// of length p, q and r
import java.io.*;
 
class GFG {
 
    // Function that returns
    // the maximum number
    // of segments possible
    static int findMaximum(int l, int p, int q, int r)
    {
 
        // Array to store the
        // cut at each length
        int dp[] = new int[l + 1];
 
        // All values with -1
        for (int i = 0; i < l + 1; i++)
            dp[i] = -1;
 
        // if length of rod is 0
        // then total cuts will
        // be 0 so, initialize
        // the dp[0] with 0
        dp[0] = 0;
 
        for (int i = 0; i <= l; i++) {
 
            // if certain length
            // is not possible
            if (dp[i] == -1)
                continue;
 
            // if a segment of
            // p is possible
            if (i + p <= l)
                dp[i + p] = Math.max(dp[i + p], dp[i] + 1);
 
            // if a segment of
            // q is possible
            if (i + q <= l)
                dp[i + q] = Math.max(dp[i + q], dp[i] + 1);
 
            // if a segment of
            // r is possible
            if (i + r <= l)
                dp[i + r] = Math.max(dp[i + r], dp[i] + 1);
        }
 
        // if no segment can be cut then return 0
        if (dp[l] == -1) {
            dp[l] = 0;
        }
        // return value corresponding
        // to length l
        return dp[l];
    }
 
    // Driver Code
    public static void main(String[] args)
    {
        int l = 11, p = 2, q = 3, r = 5;
 
        // Calling Function
        int ans = findMaximum(l, p, q, r);
        System.out.println(ans);
    }
}
 
// This code is contributed
// by anuj_67.

# Python 3 program to
# maximize the number
# of segments of length
# p, q and r
 
# Function that returns
# the maximum number
# of segments possible
 
 
def findMaximum(l, p, q, r):
 
    # Array to store the cut
    # at each length
    # All values with -1
    dp = [-1]*(l + 1)
 
    # if length of rod is 0 then
    # total cuts will be 0
    # so, initialize the dp[0] with 0
    dp[0] = 0
 
    for i in range(l+1):
 
        # if certain length is not
        # possible
        if (dp[i] == -1):
            continue
 
        # if a segment of p is possible
        if (i + p <= l):
            dp[i + p] = (max(dp[i + p],
                             dp[i] + 1))
 
        # if a segment of q is possible
        if (i + q <= l):
            dp[i + q] = (max(dp[i + q],
                             dp[i] + 1))
 
        # if a segment of r is possible
        if (i + r <= l):
            dp[i + r] = (max(dp[i + r],
                             dp[i] + 1))
 
    # if no segment can be cut then return 0
    if dp[l] == -1:
        dp[l] = 0
    # return value corresponding
    # to length l
    return dp[l]
 
 
# Driver Code
if __name__ == "__main__":
    l = 11
    p = 2
    q = 3
    r = 5
 
    # Calling Function
    ans = findMaximum(l, p, q, r)
    print(ans)
 
# This code is contributed by
# ChitraNayal

// C# program to maximize
// the number of segments
// of length p, q and r
using System;
 
class GFG {
 
    // Function that returns
    // the maximum number
    // of segments possible
    static int findMaximum(int l, int p,
                           int q, int r)
    {
 
        // Array to store the
        // cut at each length
        int[] dp = new int[l + 1];
 
        // All values with -1
        for (int i = 0; i < l + 1; i++)
            dp[i] = -1;
 
        // if length of rod is 0
        // then total cuts will
        // be 0 so, initialize
        // the dp[0] with 0
        dp[0] = 0;
 
        for (int i = 0; i <= l; i++) {
 
            // if certain length
            // is not possible
            if (dp[i] == -1)
                continue;
 
            // if a segment of
            // p is possible
            if (i + p <= l)
                dp[i + p] = Math.Max(dp[i + p],
                                     dp[i] + 1);
 
            // if a segment of
            // q is possible
            if (i + q <= l)
                dp[i + q] = Math.Max(dp[i + q],
                                     dp[i] + 1);
 
            // if a segment of
            // r is possible
            if (i + r <= l)
                dp[i + r] = Math.Max(dp[i + r],
                                     dp[i] + 1);
        }
 
        // if no segment can be cut then return 0
        if (dp[l] == -1) {
            dp[l] = 0;
        }
        // return value corresponding
        // to length l
        return dp[l];
    }
 
    // Driver Code
    public static void Main()
    {
        int l = 11, p = 2, q = 3, r = 5;
 
        // Calling Function
        int ans = findMaximum(l, p, q, r);
        Console.WriteLine(ans);
    }
}
 
// This code is contributed
// by anuj_67.

<script>
// Javascript program to maximize
// the number of segments
// of length p, q and r
     
    // Function that returns
    // the maximum number
    // of segments possible
    function findMaximum(l,p,q,r)
    {
        // Array to store the
        // cut at each length
        let dp = new Array(l + 1);
  
        // All values with -1
        for (let i = 0; i < l + 1; i++)
            dp[i] = -1;
  
        // if length of rod is 0
        // then total cuts will
        // be 0 so, initialize
        // the dp[0] with 0
        dp[0] = 0;
  
        for (let i = 0; i <= l; i++) {
  
            // if certain length
            // is not possible
            if (dp[i] == -1)
                continue;
  
            // if a segment of
            // p is possible
            if (i + p <= l)
                dp[i + p] = Math.max(dp[i + p], dp[i] + 1);
  
            // if a segment of
            // q is possible
            if (i + q <= l)
                dp[i + q] = Math.max(dp[i + q], dp[i] + 1);
  
            // if a segment of
            // r is possible
            if (i + r <= l)
                dp[i + r] = Math.max(dp[i + r], dp[i] + 1);
        }
  
        // if no segment can be cut then return 0
        if (dp[l] == -1) {
            dp[l] = 0;
        }
        // return value corresponding
        // to length l
        return dp[l];
    }
     
    // Driver Code
    let l = 11, p = 2, q = 3, r = 5;
    // Calling Function
    let ans = findMaximum(l, p, q, r);
     
    document.write(ans);
     
 
// This code is contributed by rag2127
</script>

5

Análisis de Complejidad: 

• Complejidad temporal: O(N). 
  Uso de un solo bucle for hasta la longitud ‘N’.
• Espacio Auxiliar: O(N). 
  Uso de una array ‘DP’ para realizar un seguimiento de los segmentos

Nota: Este problema también se puede considerar como un problema de cambio mínimo de monedas porque se nos da una cierta longitud para adquirir que es igual al valor de la cantidad cuyo cambio mínimo se necesita. Ahora las x, y, z son las mismas que la denominación de la moneda dada. Entonces, la longitud es lo mismo que la cantidad y xyz son lo mismo que las denominaciones, por lo tanto, solo necesitamos cambiar una condición: en lugar de encontrar el mínimo, necesitamos encontrar el máximo y obtendremos la respuesta. Como el problema del cambio mínimo de monedas es la pregunta básica de programación dinámica, esto también ayudará a resolver esta pregunta.

La condición que necesitamos cambiar en el problema de cambio mínimo de monedas

for(ll i=1;i<=n;i++)
{
     for(ll j=1;j<=3;j++)
     {
          if(i>=a[j]&&m[i-a[j]]!=-1)
          {
               dp[i]=max(dp[i],1+dp[i-a[j]]);
          }
     }
}