Dado un árbol genérico que consiste en N Nodes valorados de 0 a (N – 1) donde P[i] th en la array P[] denota i th Nodes padre (indexación basada en 1) . Cada i -ésimo Node tiene un peso adjunto, dado en la array W[] . La tarea es encontrar un par de Nodes (u, v), tales que u sea un ancestro de v , y W u – W v esté maximizado.
Nota: En la array P[] , -1 denota el Node raíz. Si hay un solo Node, imprima -1 .
Ejemplos:
Entrada: N = 4, W[] = {5, 10, 6, 12}, P[] = {2, -1, 4, 2}
Salida: 6
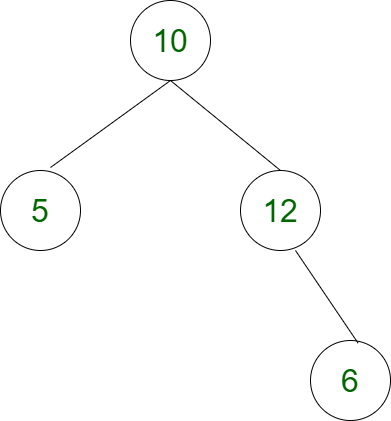
Explicación: El árbol con peso será:
Aquí, el 4 ° Node con peso 12 y el 3 ° Node con peso 6, la diferencia será (12 – 6) = 6.
Entrada: N = 1, W = { 30 }, P = { -1 }
Salida: -1
Enfoque: el problema dado se puede resolver usando la búsqueda primero en amplitud en el árbol N-ario para marcar el número de antepasado para el árbol dado P[] , y luego usando DFS Traversal y encontrar la diferencia máxima maxDiff , considerando cada Node como un antepasado con sus Nodes correspondientes que tienen menos valor de antepasado numérico. Siga los pasos a continuación para resolver el problema:
- Defina una función dfs(int src, int val, vector<int> & W) y realice las siguientes tareas:
- Establezca el valor de visited[src] como verdadero .
- Itere sobre el rango [0, tamaño) donde tamaño es el tamaño del árbol de filas [cur] usando la variable vecino y realiza las siguientes tareas:
- Si el [vecino] visitado es falso y el antepasado [vecino] es mayor que el antepasado [fuente] , establezca el valor de maxDiff como el máximo de maxDiff o val – W[vecino-1] .
- Llame a la función dfs(vecino, val, W) .
- Defina una función bfs(int src, int N) y realice las siguientes tareas:
- Asigne el vector visitado[N + 1] con valores falsos.
- Inicializar una cola q[] .
- Establezca el valor de ancestorNum[src] como 0 y visited[src] como verdadero .
- Ponga en cola el valor src en la cola q[] .
- Atraviese un ciclo while hasta que la cola q[] no esté vacía y realice las siguientes tareas:
- Inicialice la variable cur como el elemento frontal de la cola q[] y elimine la cola de la cola q[].
- Itere sobre el rango [0, tamaño) donde el tamaño es el tamaño del árbol de filas [cur] usando la variable vecino y si visitado [vecino] es falso , configúrelo como verdadero y colóquelo en la cola q [] y configure el valor de ancestro[vecino] como (ancestro[cur] + 1) .
- Inicialice los vectores tree[][],visited[] y ancestorNum[] .
- Inicialice la variable maxDiff como INT_MIN para almacenar la respuesta.
- Cambie el tamaño del vector tree[][] al tamaño (N + 1) .
- Asigne vectores visitados[N + 1] con valor falso y ancestroNum[N+1] con valor 0 .
- Inicialice la variable src .
- Iterar sobre el rango [0, N) usando la variable i y si P[ I ] es -1 , entonces establezca el valor de src como i . De lo contrario, introduzca el valor P[ I ] en la fila i+1 y el valor i + 1 en la fila P[ I ] en el vector tree[][] .
- Llame a la función bfs(src, N+1) para realizar una búsqueda en amplitud.
- Asigne el vector visitado[N+1] con valor falso .
- Llame a la función dfs(src, W[src], W) para realizar una búsqueda en profundidad.
- Iterar sobre el rango [0, N) usando la variable i y realizar los siguientes pasos:
- Si i es igual a src , entonces continúe . De lo contrario, asigne el vector visitado[N+1] con valor false .
- Llame a la función dfs(i+1, W[i], W) .
- Después de realizar los pasos anteriores, imprima el valor de maxDiff como respuesta.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
vector<vector<int> > tree;
vector<bool> visited;
vector<int> ancestorNum;
// Stores the maximum difference
int maxDiff = INT_MIN;
// DFS traversal for source node as src
void dfs(int src, int val, vector<int>& W)
{
// Mark src node as visited
visited[src] = true;
// Traverse the tree
for (auto neighbour : tree[src]) {
// Check neighbour node is not
// visited and ancestorNum should
// be greater than the src node
if (!visited[neighbour]
&& (ancestorNum[neighbour]
> ancestorNum[src])) {
// Update the maxDiff
maxDiff = max(
val - W[neighbour - 1],
maxDiff);
// Recurrence call for dfs
dfs(neighbour, val, W);
}
}
}
// BFS traversal for source node as src
void bfs(int src, int N)
{
// Initially mark all node as
// not visited
visited.assign(N, false);
// Stores the nodes
queue<int> q;
// Initially for src node mark
// ancestorNum as 0
ancestorNum[src] = 0;
// Mark src as visited
visited[src] = true;
// Push src node into the q
q.push(src);
// Traverse the queue q
while (!q.empty()) {
// Pop front element of the q
int cur = q.front();
q.pop();
// Traverse the tree
for (auto neighbour : tree[cur]) {
// Check neighbour node is
// already not visited
if (!visited[neighbour]) {
// Mark the neighbour
// node as visited
visited[neighbour] = true;
// Push the neighbour
// node into the q
q.push(neighbour);
// Update the neighbour
// node ancestorNum
ancestorNum[neighbour]
= ancestorNum[cur] + 1;
}
}
}
}
// Function to find the maximized
// difference between two pair of nodes
// in rooted tree such that one node
// is ancestor of another node
void maximumDiff(vector<int> W,
vector<int> P, int N)
{
if (N == 1) {
cout << "-1\n";
return;
}
// Resize the tree
tree.resize(N + 1);
// Mark all the nodes as not visited
visited.assign(N + 1, false);
// Assign all the node values
// for ancestorNum to 0
ancestorNum.assign(N + 1, 0);
// Stores the source node to traverse
int src;
for (int i = 0; i < N; i++) {
// Check P[i] is -1
if (P[i] == -1)
// Update the source node src
src = i;
else {
// Store the tree values
tree[i + 1].push_back(P[i]);
tree[P[i]].push_back(i + 1);
}
}
// BFS from the source node src
bfs(src, N + 1);
// Mark all the nodes as not visited
visited.assign(N + 1, false);
// DFS Call for source node src
dfs(src, W[src], W);
// For every node call dfs function
for (int i = 0; i < N; i++) {
// Check i is root node
if (i == src)
continue;
// Mark all the nodes as
// not visited
visited.assign(N + 1, false);
// DFS Call for source
// node as i+1
dfs(i + 1, W[i], W);
}
// Print the maxDiff
cout << maxDiff << endl;
}
// Driver Code
int main()
{
vector<int> W = { 5, 10, 6, 12 };
vector<int> P = { 2, -1, 4, 2 };
int N = P.size();
maximumDiff(W, P, N);
return 0;
}
Python3
# Python 3 program for the above approach
tree = []
visited = []
ancestorNum = []
import sys
# Stores the maximum difference
maxDiff = -sys.maxsize - 1
# DFS traversal for source node as src
def dfs(src, val, W):
global ancestorNum
global visited
global tree
global maxDiff
# Mark src node as visited
visited[src] = True
# Traverse the tree
for neighbour in tree[src]:
# Check neighbour node is not
# visited and ancestorNum should
# be greater than the src node
if (visited[neighbour] == False and (ancestorNum[neighbour]> ancestorNum[src])):
# Update the maxDiff
maxDiff = max(val - W[neighbour - 1],maxDiff)
# Recurrence call for dfs
dfs(neighbour, val, W)
# BFS traversal for source node as src
def bfs(src,N):
global ancestorNum
global visited
global tree
# Initially mark all node as
# not visited
visited = [False for i in range(N)]
# Stores the nodes
q = []
# Initially for src node mark
# ancestorNum as 0
ancestorNum[src] = 0
# Mark src as visited
visited[src] = True
# Push src node into the q
q.append(src)
# Traverse the queue q
while (len(q)>0):
# Pop front element of the q
cur = q[0]
q = q[1:]
# Traverse the tree
for neighbour in tree[cur]:
# Check neighbour node is
# already not visited
if (visited[neighbour]==False):
# Mark the neighbour
# node as visited
visited[neighbour] = True
# Push the neighbour
# node into the q
q.append(neighbour)
# Update the neighbour
# node ancestorNum
ancestorNum[neighbour] = ancestorNum[cur] + 1
# Function to find the maximized
# difference between two pair of nodes
# in rooted tree such that one node
# is ancestor of another node
def maximumDiff(W, P, N):
global ancestorNum
global visited
global tree
if (N == 1):
print("-1")
return
# Resize the tree
tree = [[] for i in range(N+1)]
# Mark all the nodes as not visited
visited = [False for i in range(N + 1)]
# Assign all the node values
# for ancestorNum to 0
ancestorNum = [0 for i in range(N + 1)]
# Stores the source node to traverse
src = 0
for i in range(N):
# Check P[i] is -1
if (P[i] == -1):
# Update the source node src
src = i
else:
# Store the tree values
tree[i + 1].append(P[i])
tree[P[i]].append(i + 1)
# BFS from the source node src
bfs(src, N + 1)
# Mark all the nodes as not visited
visited = [False for i in range(N+1)]
# DFS Call for source node src
dfs(src, W[src], W)
# For every node call dfs function
for i in range(N):
# Check i is root node
if (i == src):
continue
# Mark all the nodes as
# not visited
visited = [False for i in range(N+1)]
# DFS Call for source
# node as i+1
dfs(i + 1, W[i], W)
# Print the maxDiff
print(maxDiff)
# Driver Code
if __name__ == '__main__':
W = [5, 10, 6, 12]
P = [2, -1, 4, 2]
N = len(P)
maximumDiff(W, P, N)
# This code is contributed by SURENDRA_GANGWAR.
6
Tiempo Complejidad: O(N 2 )
Espacio Auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por dharanendralv23 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA