Dada una array arr[] que consta de N elementos no negativos y un número entero X , la tarea es hacer incrementos de X tales que el valor de la array sume cuando cada elemento se divida por 10, es decir
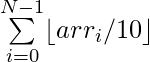
se maximiza. Imprime el valor máximo de
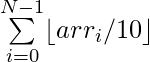
posible.
Nota: El valor de cualquier elemento no se puede aumentar más allá de 1000.
Ejemplos:
Entrada: N = 4, X = 6, arr[] = {4, 8, 8, 8}
Salida: 3
Explicación:
Convierta la array dada en {4, 10, 10, 10} incrementando arr[1], arr [2] y arr[3] dos veces cada uno.
Ahora
es 0 + 1 + 1 + 1 = 3.
Entrada: N = 3, X = 122, arr[] = {3, 11, 14}
Salida: 15
Acercarse:
- Para todos los elementos, calcule la cantidad de incrementos necesarios para aumentar el número al siguiente múltiplo de 10 y almacene estos valores en una array, digamos V .
- Calcule el número máximo de veces que un elemento se puede incrementar en 10 y mantenga su valor <= 1000 y agregue este valor a una variable, digamos incrementos que se inicializa en 0.
- Ordene la array V para que no sea decreciente.
- Luego, para cada valor en V , realice los movimientos requeridos y aumente algún elemento al siguiente múltiplo de 10, esto aumenta la respuesta en 1.
- Haga esto, mientras el total de movimientos realizados no exceda X .
- Después de pasar por todos los elementos de V , si aún quedan algunos movimientos, agregue al mínimo de respuesta entre incrementos y (movimientos restantes)/10 .
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above problem
#include <bits/stdc++.h>
using namespace std;
void maximizeval10(int a[],
int n, int k)
{
// initialize variables
int increments = 0;
int ans = 0;
vector<int> v;
for (int i = 0; i < n; i++) {
// add the current
// contribution of the
// element to the answer
ans += (a[i] / 10);
// if the value is
// already maximum
// then we can't change it
if (a[i] == 1000)
continue;
else {
// moves required to move
// to the next multiple
// of 10
v.push_back(10 - a[i] % 10);
// no of times we can
// add 10 to this value
// so that its value
// does not exceed 1000.
increments += (100
- ((a[i]) / 10)
- 1);
}
}
// sort the array
sort(v.begin(), v.end());
int sum = 0;
for (int i = 0; i < v.size();
i++) {
// adding the values to
// increase the numbers
// to the next multiple of 10
sum += v[i];
if (sum <= k) {
// if the total moves
// are less than X then
// increase the answer
ans++;
}
else
// if the moves exceed
// X then we cannot
// increase numbers
break;
}
// if there still remain
// some moves
if (sum < k) {
// remaining moves
int remaining = k - sum;
// add minimum of increments and
// remaining/10 to the
// answer
ans += min(increments,
remaining / 10);
}
// output the final answer
cout << ans;
}
// Driver Code
int main()
{
int N = 4;
int X = 6;
int A[N] = { 4, 8, 8, 8 };
maximizeval10(A, N, X);
return 0;
}
Java
// Java program for the above approach
import java.util.*;
class GFG{
public static void maximizeval10(int[] a, int n,
int k)
{
// Initialize variables
int increments = 0;
int ans = 0;
Vector<Integer> v = new Vector<>();
for(int i = 0; i < n; i++)
{
// Add the current
// contribution of the
// element to the answer
ans += (a[i] / 10);
// If the value is
// already maximum
// then we can't change it
if (a[i] == 1000)
continue;
else
{
// Moves required to move
// to the next multiple
// of 10
v.add(10 - a[i] % 10);
// No of times we can
// add 10 to this value
// so that its value
// does not exceed 1000.
increments += (100 - ((a[i]) /
10) - 1);
}
}
// Sort the array
Collections.sort(v);
int sum = 0;
for(int i = 0; i < v.size(); i++)
{
// Adding the values to
// increase the numbers
// to the next multiple of 10
sum += v.get(i);
if (sum <= k)
{
// If the total moves
// are less than X then
// increase the answer
ans++;
}
else
// If the moves exceed
// X then we cannot
// increase numbers
break;
}
// If there still remain
// some moves
if (sum < k)
{
// Remaining moves
int remaining = k - sum;
// Add minimum of increments and
// remaining/10 to the
// answer
ans += Math.min(increments,
remaining / 10);
}
// Output the final answer
System.out.print(ans);
}
// Driver code
public static void main(String[] args)
{
int N = 4;
int X = 6;
int A[] = { 4, 8, 8, 8 };
maximizeval10(A, N, X);
}
}
// This code is contributed by divyeshrabadiya07
Python3
# Python3 program for the above problem def maximizeval10(a, n, k): # Initialize variables increments = 0 ans = 0 v = [] for i in range (n): # Add the current # contribution of the # element to the answer ans += (a[i] // 10) # If the value is already # maximum then we can't # change it if (a[i] == 1000): continue else: # Moves required to move # to the next multiple # of 10 v.append(10 - a[i] % 10) # No of times we can # add 10 to this value # so that its value # does not exceed 1000. increments += (100 - ((a[i]) // 10) - 1); # Sort the array v.sort() sum = 0 for i in range(len(v)): # Adding the values to # increase the numbers # to the next multiple of 10 sum += v[i] if (sum <= k): # If the total moves # are less than X then # increase the answer ans += 1 else: # If the moves exceed # X then we cannot # increase numbers break # If there still remain # some moves if (sum < k): # Remaining moves remaining = k - sum # Add minimum of increments # and remaining/10 to the # answer ans += min(increments, remaining // 10) # Output the final answer print(ans) # Driver Code if __name__ =="__main__": N = 4 X = 6 A = [ 4, 8, 8, 8 ] maximizeval10(A, N, X) # This code is contributed by chitranayal
C#
// C# program for the above approach
using System;
using System.Collections.Generic;
class GFG{
public static void maximizeval10(int[] a,
int n,
int k)
{
// Initialize variables
int increments = 0;
int ans = 0;
List<int> v = new List<int>();
for(int i = 0; i < n; i++)
{
// Add the current
// contribution of the
// element to the answer
ans += (a[i] / 10);
// If the value is
// already maximum
// then we can't change it
if (a[i] == 1000)
continue;
else
{
// Moves required to move
// to the next multiple
// of 10
v.Add(10 - a[i] % 10);
// No of times we can
// add 10 to this value
// so that its value
// does not exceed 1000.
increments += (100 - ((a[i]) /
10) - 1);
}
}
// Sort the array
v.Sort();
int sum = 0;
for(int i = 0; i < v.Count; i++)
{
// Adding the values to
// increase the numbers
// to the next multiple of 10
sum += v[i];
if (sum <= k)
{
// If the total moves
// are less than X then
// increase the answer
ans++;
}
else
// If the moves exceed
// X then we cannot
// increase numbers
break;
}
// If there still remain
// some moves
if (sum < k)
{
// Remaining moves
int remaining = k - sum;
// Add minimum of increments and
// remaining/10 to the
// answer
ans += Math.Min(increments,
remaining / 10);
}
// Output the readonly answer
Console.Write(ans);
}
// Driver code
public static void Main(String[] args)
{
int N = 4;
int X = 6;
int []A = {4, 8, 8, 8};
maximizeval10(A, N, X);
}
}
// This code is contributed by shikhasingrajput
Javascript
<script>
// Javascript program for the above approach
function maximizeval10(a,n,k)
{
// Initialize variables
let increments = 0;
let ans = 0;
let v = [];
for(let i = 0; i < n; i++)
{
// Add the current
// contribution of the
// element to the answer
ans += Math.floor(a[i] / 10);
// If the value is
// already maximum
// then we can't change it
if (a[i] == 1000)
continue;
else
{
// Moves required to move
// to the next multiple
// of 10
v.push(10 - a[i] % 10);
// No of times we can
// add 10 to this value
// so that its value
// does not exceed 1000.
increments += (100 - (Math.floor(a[i]) / 10) - 1);
}
}
// Sort the array
v.sort(function(a,b){return a-b;});
let sum = 0;
for(let i = 0; i < v.length; i++)
{
// Adding the values to
// increase the numbers
// to the next multiple of 10
sum += v[i];
if (sum <= k)
{
// If the total moves
// are less than X then
// increase the answer
ans++;
}
else
// If the moves exceed
// X then we cannot
// increase numbers
break;
}
// If there still remain
// some moves
if (sum < k)
{
// Remaining moves
let remaining = k - sum;
// Add minimum of increments and
// remaining/10 to the
// answer
ans += Math.min(increments,
Math.floor(remaining / 10));
}
// Output the final answer
document.write(ans);
}
// Driver code
let N = 4;
let X = 6;
let A=[4, 8, 8, 8];
maximizeval10(A, N, X);
// This code is contributed by avanitrachhadiya2155
</script>
3
Complejidad de tiempo: O(N * log(N))
Complejidad de espacio auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por nishitsharma1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA