Dadas dos arrays ordenadas, a[] y b[], la tarea es encontrar la mediana de estas arrays ordenadas, en O(log(min(n, m)), cuando n es el número de elementos en la primera array, y m es el número de elementos en la segunda array
Requisito previo: Mediana de dos arrays ordenadas de diferentes tamaños.
Ejemplos:
Input : ar1[] = {-5, 3, 6, 12, 15}
ar2[] = {-12, -10, -6, -3, 4, 10}
The merged array is :
ar3[] = {-12, -10, -6, -5 , -3,
3, 4, 6, 10, 12, 15}
Output : The median is 3.
Input : ar1[] = {2, 3, 5, 8}
ar2[] = {10, 12, 14, 16, 18, 20}
The merged array is :
ar3[] = {2, 3, 5, 8, 10, 12, 14, 16, 18, 20}
if the number of the elements are even,
so there are two middle elements,
take the average between the two :
(10 + 12) / 2 = 11.
Output : The median is 11.
Nota: en el caso de números pares en total y si queremos devolver una mediana que existe en la array fusionada, podemos devolver el elemento en la posición (n+m)/2 o (n+m)/2 – 1. En ese caso, la mediana puede ser 10 o 12.
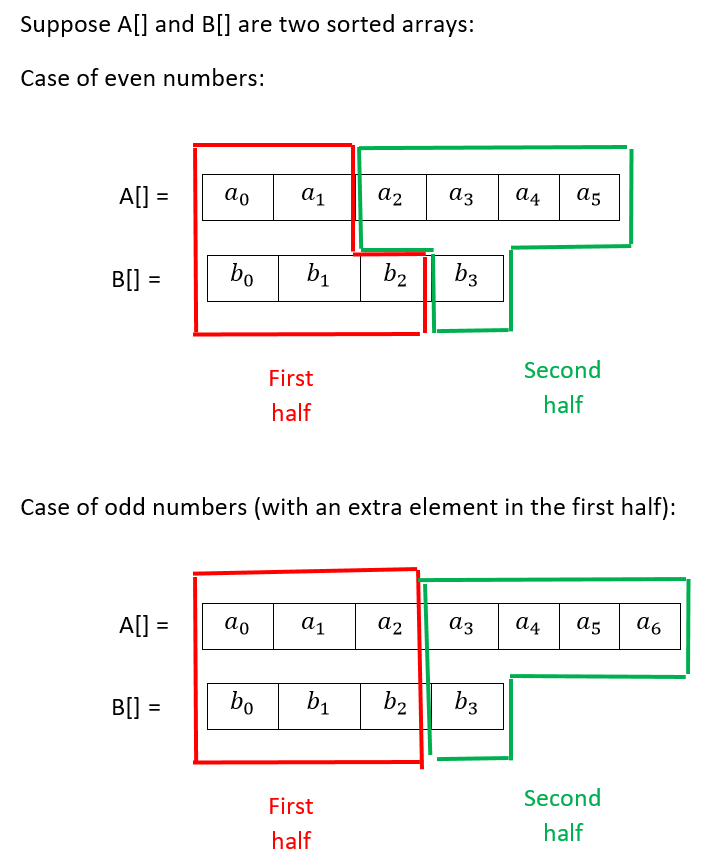
Enfoque: comience a dividir las dos arrays en dos grupos de mitades (no dos partes, pero ambas particiones deben tener la misma cantidad de elementos). La primera mitad contiene algunos primeros elementos de la primera y la segunda array, y la segunda mitad contiene el resto (o el último) elementos de la primera y la segunda array. Debido a que las arrays pueden ser de diferentes tamaños, no significa tomar cada mitad de cada array. El siguiente ejemplo aclara la explicación. Llegar a una condición tal que cada elemento de la primera mitad sea menor o igual que cada elemento de la segunda mitad.
¿Cómo llegar a esta condición?
Ejemplo en el caso de números pares. Supongamos que se encuentra la partición. Como A[] y B[] son dos arrays ordenadas, a1 es menor o igual que a2 y b2 es menor o igual que b3. Ahora, para comprobar si a1 es menor o igual que b3, y si b2 es menor o igual que a2. Si ese es el caso, significa que todos los elementos de la primera mitad son menores o iguales que todos los elementos de la segunda mitad, porque a1 es mayor o igual que todos los elementos anteriores (a0) en A[], y b2 es mayor o igual que todos los elementos anteriores (b1 y b0) en B[]. En el caso de números pares en total, la mediana será el promedio entre el máximo de a1, b2 y el mínimo de a2, b3, pero en el caso de números impares en total, la mediana será el máximo de a2, b2. Pero si no son estos dos casos, hay dos opciones (en referencia al ejemplo de números pares):
b2 > a2 o a1 > b3
si b2 > a2 significa eso, busque en el lado derecho del arreglo, y si a1 > b3 significa eso, busque en el lado izquierdo del arreglo, hasta encontrar la condición deseada.
¿Por qué la condición anterior conduce a la mediana?
La mediana es el (n + 1)/2 elemento más pequeño de la array, y aquí, la mediana es el (n + m + 1)/2 elemento más pequeño entre las dos arrays. Si todos los elementos de la primera mitad son menores (o iguales) que todos los elementos de la segunda mitad, en caso de que el total sea un número impar, solo calcule el máximo entre los dos últimos elementos de la primera mitad (a2 y b2 en nuestro ejemplo), y esto nos llevará al (n + m + 1) / 2 elemento más pequeño entre las dos arrays, que es la mediana ((7 + 4 + 1) / 2 = 6). Pero en caso de números pares en total, calcule el promedio entre el máximo de los dos últimos elementos en la primera mitad (a1 y b2 en nuestro ejemplo) con su número sucesivo entre las arrays que es el mínimo de los dos primeros elementos en la segunda mitad (a2 y b3 en nuestro ejemplo).
El proceso de la partición:
Para hacer dos mitades, haga la partición tal que el índice que divide la array A[] + el índice que divide la array B[] son iguales al número total de elementos más uno dividido por 2, es decir (n + m + 1) / 2 (+1 es, si el número total de elementos es impar).
Primero, defina dos variables: min_index y max_index, e inicialice min_index a 0 y max_index a la longitud de la array más pequeña. En estos ejemplos a continuación, A[] es la array más pequeña.
Para particionar A[], use la fórmula (min_index + max_index) / 2 e insértela en una variable i. Para particionar B[], use la fórmula (n + m + 1) / 2 – i e insértela en una variable j.
la variable i significa el número de elementos que se insertarán desde A[] en la primera mitad, y j significa el número de elementos que se insertarán desde B[] en la primera mitad, el resto de los elementos se insertarán en la segunda mitad.
Echa un vistazo a los siguientes ejemplos:
Nota: la partición no funcionó si alguna array está vacía de las arrays dadas:
Por ejemplo: si arr1=[2], arr2=[] con esta fórmula “(n + m + 1) / 2” el valor de i=0 y el valor de j=1 y esto le da un error de índice porque arr2 está vacío y arr2[j] le da un error de índice. Debe manejar este caso verificando si una array está vacía, simplemente puede devolver el medio de otra array.
por ejemplo: si la longitud de arr1 es 0:
mediana de retorno de arr2
de lo contrario, si la longitud de arr2 es 0:
devolver la mediana de arr1
Ejemplo 1 :


Ejemplo 2 (Este ejemplo se refiere a la condición que devuelve una mediana que existe en la array fusionada) :



A continuación se muestra la implementación del enfoque anterior:
C++
// CPP code for median with case of returning
// double value when even number of elements are
// present in both array combinely
#include<bits/stdc++.h>
using std::cout;
int maximum(int a, int b);
int minimum(int a, int b);
// Function to find median of two sorted arrays
double findMedianSortedArrays(int *a, int n,
int *b, int m)
{
int min_index = 0, max_index = n, i, j, median;
while (min_index <= max_index)
{
i = (min_index + max_index) / 2;
j = ((n + m + 1) / 2) - i;
// If j is negative then the partition is not
// possible having i elements from array i
if (j < 0)
{
max_index = i-1;
continue;
}
// if i = n, it means that Elements from a[] in
// the second half is an empty set. and if j = 0,
// it means that Elements from b[] in the first
// half is an empty set. so it is necessary to
// check that, because we compare elements from
// these two groups.
// Searching on right
if (i < n && j > 0 && b[j - 1] > a[i])
min_index = i + 1;
// if i = 0, it means that Elements from a[] in
// the first half is an empty set and if j = m,
// it means that Elements from b[] in the second
// half is an empty set. so it is necessary to
// check that, because we compare elements
// from these two groups.
// searching on left
else if (i > 0 && j < m && b[j] < a[i - 1])
max_index = i - 1;
// we have found the desired halves.
else
{
// this condition happens when we don't have any
// elements in the first half from a[] so we
// returning the last element in b[] from
// the first half.
if (i == 0)
median = b[j - 1];
// and this condition happens when we don't
// have any elements in the first half from
// b[] so we returning the last element in
// a[] from the first half.
else if (j == 0)
median = a[i - 1];
else
median = maximum(a[i - 1], b[j - 1]);
break;
}
}
// calculating the median.
// If number of elements is odd there is
// one middle element.
if ((n + m) % 2 == 1)
return (double)median;
// Elements from a[] in the second half is an empty set.
if (i == n)
return (median+b[j]) / 2.0;
// Elements from b[] in the second half is an empty set.
if (j == m)
return (median + a[i]) / 2.0;
return (median + minimum(a[i], b[j])) / 2.0;
}
// Function to find max
int maximum(int a, int b)
{
return a > b ? a : b;
}
// Function to find minimum
int minimum(int a, int b)
{
return a < b ? a : b;
}
// Driver code
int main()
{
int a[] = {900};
int b[] = { 10, 13, 14};
int n = sizeof(a) / sizeof(int);
int m = sizeof(b) / sizeof(int);
// we need to define the smaller array as the
// first parameter to make sure that the
// time complexity will be O(log(min(n,m)))
if (n < m)
cout << "The median is : "
<< findMedianSortedArrays(a, n, b, m);
else
cout << "The median is : "
<< findMedianSortedArrays(b, m, a, n);
return 0;
}
Java
// Java code for median with
// case of returning double
// value when even number of
// elements are present in
// both array combinely
import java.io.*;
class GFG
{
static int []a = new int[]{900};
static int []b = new int[]{10, 13, 14};
// Function to find max
static int maximum(int a, int b)
{
return a > b ? a : b;
}
// Function to find minimum
static int minimum(int a, int b)
{
return a < b ? a : b;
}
// Function to find median
// of two sorted arrays
static double findMedianSortedArrays(int n,
int m)
{
int min_index = 0,
max_index = n, i = 0,
j = 0, median = 0;
while (min_index <= max_index)
{
i = (min_index + max_index) / 2;
j = ((n + m + 1) / 2) - i;
// if i = n, it means that Elements
// from a[] in the second half is an
// empty set. and if j = 0, it means
// that Elements from b[] in the first
// half is an empty set. so it is
// necessary to check that, because we
// compare elements from these two
// groups. Searching on right
if (i < n && j > 0 && b[j - 1] > a[i])
min_index = i + 1;
// if i = 0, it means that Elements
// from a[] in the first half is an
// empty set and if j = m, it means
// that Elements from b[] in the second
// half is an empty set. so it is
// necessary to check that, because
// we compare elements from these two
// groups. searching on left
else if (i > 0 && j < m && b[j] < a[i - 1])
max_index = i - 1;
// we have found the desired halves.
else
{
// this condition happens when we
// don't have any elements in the
// first half from a[] so we
// returning the last element in
// b[] from the first half.
if (i == 0)
median = b[j - 1];
// and this condition happens when
// we don't have any elements in the
// first half from b[] so we
// returning the last element in
// a[] from the first half.
else if (j == 0)
median = a[i - 1];
else
median = maximum(a[i - 1],
b[j - 1]);
break;
}
}
// calculating the median.
// If number of elements is odd
// there is one middle element.
if ((n + m) % 2 == 1)
return (double)median;
// Elements from a[] in the
// second half is an empty set.
if (i == n)
return (median + b[j]) / 2.0;
// Elements from b[] in the
// second half is an empty set.
if (j == m)
return (median + a[i]) / 2.0;
return (median + minimum(a[i],
b[j])) / 2.0;
}
// Driver code
public static void main(String args[])
{
int n = a.length;
int m = b.length;
// we need to define the
// smaller array as the
// first parameter to
// make sure that the
// time complexity will
// be O(log(min(n,m)))
if (n < m)
System.out.print("The median is : " +
findMedianSortedArrays(n, m));
else
System.out.print("The median is : " +
findMedianSortedArrays(m, n));
}
}
// This code is contributed by
// Manish Shaw(manishshaw1)
Python3
# Python code for median with
# case of returning double
# value when even number
# of elements are present
# in both array combinely
median = 0
i = 0
j = 0
# def to find max
def maximum(a, b):
return a if a > b else b
# def to find minimum
def minimum(a, b):
return a if a < b else b
# def to find median
# of two sorted arrays
def findMedianSortedArrays(a, n, b, m):
# if a is empty
if n==0:
# if b has even no. of elements
if m%2==0:
return (b[m/2]+b[(m/2)+1])/2
# if b has odd no. of elements
else:
return b[int(m/2)]
# if b is empty
elif m==0:
# if a has even no. of elements
if n%2==0:
return (a[n/2]+a[(n/2)+1])/2
# if a has odd no. of elements
else:
return a[int(n/2)]
global median, i, j
min_index = 0
max_index = n
while (min_index <= max_index):
i = int((min_index + max_index) / 2)
j = int(((n + m + 1) / 2) - i)
# if i = n, it means that
# Elements from a[] in the
# second half is an empty
# set. and if j = 0, it
# means that Elements from
# b[] in the first half is
# an empty set. so it is
# necessary to check that,
# because we compare elements
# from these two groups.
# Searching on right
if (i < n and j > 0 and b[j - 1] > a[i]):
min_index = i + 1
# if i = 0, it means that
# Elements from a[] in the
# first half is an empty
# set and if j = m, it means
# that Elements from b[] in
# the second half is an empty
# set. so it is necessary to
# check that, because we compare
# elements from these two groups.
# searching on left
elif (i > 0 and j < m and b[j] < a[i - 1]):
max_index = i - 1
# we have found the
# desired halves.
else:
# this condition happens when
# we don't have any elements
# in the first half from a[]
# so we returning the last
# element in b[] from the
# first half.
if (i == 0):
median = b[j - 1]
# and this condition happens
# when we don't have any
# elements in the first half
# from b[] so we returning the
# last element in a[] from the
# first half.
elif (j == 0):
median = a[i - 1]
else:
median = maximum(a[i - 1], b[j - 1])
break
# calculating the median.
# If number of elements
# is odd there is
# one middle element.
if ((n + m) % 2 == 1):
return median
# Elements from a[] in the
# second half is an empty set.
if (i == n):
return ((median + b[j]) / 2.0)
# Elements from b[] in the
# second half is an empty set.
if (j == m):
return ((median + a[i]) / 2.0)
return ((median + minimum(a[i], b[j])) / 2.0)
# Driver code
a = [900]
b = [10, 13, 14]
n = len(a)
m = len(b)
# we need to define the
# smaller array as the
# first parameter to make
# sure that the time complexity
# will be O(log(min(n,m)))
if (n < m):
print("The median is : {}".format(findMedianSortedArrays(a, n, b, m)))
else:
echo("The median is : {}".format(findMedianSortedArrays(b, m, a, n)))
# This code is contributed
# by Aditya Khare(adityaskhare123)
C#
// C# code for median with case of returning
// double value when even number of elements
// are present in both array combinely
using System;
class GFG {
// Function to find max
static int maximum(int a, int b)
{
return a > b ? a : b;
}
// Function to find minimum
static int minimum(int a, int b)
{
return a < b ? a : b;
}
// Function to find median of two sorted
// arrays
static double findMedianSortedArrays(ref int []a,
int n, ref int []b, int m)
{
int min_index = 0, max_index = n, i = 0,
j = 0, median = 0;
while (min_index <= max_index)
{
i = (min_index + max_index) / 2;
j = ((n + m + 1) / 2) - i;
// if i = n, it means that Elements
// from a[] in the second half is an
// empty set. and if j = 0, it means
// that Elements from b[] in the first
// half is an empty set. so it is
// necessary to check that, because we
// compare elements from these two
// groups. Searching on right
if (i < n && j > 0 && b[j - 1] > a[i])
min_index = i + 1;
// if i = 0, it means that Elements
// from a[] in the first half is an
// empty set and if j = m, it means
// that Elements from b[] in the second
// half is an empty set. so it is
// necessary to check that, because
// we compare elements from these two
// groups. searching on left
else if (i > 0 && j < m && b[j] < a[i - 1])
max_index = i - 1;
// we have found the desired halves.
else
{
// this condition happens when we
// don't have any elements in the
// first half from a[] so we
// returning the last element in
// b[] from the first half.
if (i == 0)
median = b[j - 1];
// and this condition happens when
// we don't have any elements in the
// first half from b[] so we
// returning the last element in
// a[] from the first half.
else if (j == 0)
median = a[i - 1];
else
median = maximum(a[i - 1], b[j - 1]);
break;
}
}
// calculating the median.
// If number of elements is odd
// there is one middle element.
if ((n + m) % 2 == 1)
return (double)median;
// Elements from a[] in the second
// half is an empty set.
if (i == n)
return (median+b[j]) / 2.0;
// Elements from b[] in the second
// half is an empty set.
if (j == m)
return (median + a[i]) / 2.0;
return (median + minimum(a[i], b[j])) / 2.0;
}
// Driver code
static void Main()
{
int []a = new int[]{900};
int []b = new int[]{ 10, 13, 14};
int n = a.Length;
int m = b.Length;
// we need to define the smaller
// array as the first parameter to
// make sure that the time
// complexity will be O(log(min(n,m)))
if (n < m)
Console.Write("The median is : "
+ findMedianSortedArrays(ref a, n,
ref b, m));
else
Console.Write("The median is : "
+ findMedianSortedArrays(ref b, m,
ref a, n));
}
}
// This code is contributed by Manish Shaw
// (manishshaw1)
PHP
<?php
// PHP code for median with
// case of returning double
// value when even number
// of elements are present
// in both array combinely
$median = 0;
$i = 0; $j = 0;
// Function to find max
function maximum($a, $b)
{
return $a > $b ? $a : $b;
}
// Function to find minimum
function minimum($a, $b)
{
return $a < $b ? $a : $b;
}
// Function to find median
// of two sorted arrays
function findMedianSortedArrays(&$a, $n,
&$b, $m)
{
global $median, $i, $j;
$min_index = 0;
$max_index = $n;
while ($min_index <= $max_index)
{
$i = intval(($min_index +
$max_index) / 2);
$j = intval((($n + $m + 1) /
2) - $i);
// if i = n, it means that
// Elements from a[] in the
// second half is an empty
// set. and if j = 0, it
// means that Elements from
// b[] in the first half is
// an empty set. so it is
// necessary to check that,
// because we compare elements
// from these two groups.
// Searching on right
if ($i < $n && $j > 0 &&
$b[$j - 1] > $a[$i])
$min_index = $i + 1;
// if i = 0, it means that
// Elements from a[] in the
// first half is an empty
// set and if j = m, it means
// that Elements from b[] in
// the second half is an empty
// set. so it is necessary to
// check that, because we compare
// elements from these two groups.
// searching on left
else if ($i > 0 && $j < $m &&
$b[$j] < $a[$i - 1])
$max_index = $i - 1;
// we have found the
// desired halves.
else
{
// this condition happens when
// we don't have any elements
// in the first half from a[]
// so we returning the last
// element in b[] from the
// first half.
if ($i == 0)
$median = $b[$j - 1];
// and this condition happens
// when we don't have any
// elements in the first half
// from b[] so we returning the
// last element in a[] from the
// first half.
else if ($j == 0)
$median = $a[$i - 1];
else
$median = maximum($a[$i - 1],
$b[$j - 1]);
break;
}
}
// calculating the median.
// If number of elements
// is odd there is
// one middle element.
if (($n + $m) % 2 == 1)
return $median;
// Elements from a[] in the
// second half is an empty set.
if ($i == $n)
return (($median +
$b[$j]) / 2.0);
// Elements from b[] in the
// second half is an empty set.
if ($j == $m)
return (($median +
$a[$i]) / 2.0);
return (($median +
minimum($a[$i],
$b[$j])) / 2.0);
}
// Driver code
$a = array(900);
$b = array(10, 13, 14);
$n = count($a);
$m = count($b);
// we need to define the
// smaller array as the
// first parameter to make
// sure that the time complexity
// will be O(log(min(n,m)))
if ($n < $m)
echo ("The median is : " .
findMedianSortedArrays($a, $n,
$b, $m));
else
echo ("The median is : " .
findMedianSortedArrays($b, $m,
$a, $n));
// This code is contributed
// by Manish Shaw(manishshaw1)
?>
Javascript
<script>
// Javascript code for median with
// case of returning double
// value when even number of
// elements are present in
// both array combinely
let a=[900];
let b=[10, 13, 14];
// Function to find max
function maximum(a,b)
{
return a > b ? a : b;
}
// Function to find minimum
function minimum(a,b)
{
return a < b ? a : b;
}
// Function to find median
// of two sorted arrays
function findMedianSortedArrays(n,m)
{
let min_index = 0,
max_index = n, i = 0,
j = 0, median = 0;
while (min_index <= max_index)
{
i = Math.floor((min_index + max_index) / 2);
j = Math.floor((n + m + 1) / 2) - i;
// if i = n, it means that Elements
// from a[] in the second half is an
// empty set. and if j = 0, it means
// that Elements from b[] in the first
// half is an empty set. so it is
// necessary to check that, because we
// compare elements from these two
// groups. Searching on right
if (i < n && j > 0 && b[j - 1] > a[i])
min_index = i + 1;
// if i = 0, it means that Elements
// from a[] in the first half is an
// empty set and if j = m, it means
// that Elements from b[] in the second
// half is an empty set. so it is
// necessary to check that, because
// we compare elements from these two
// groups. searching on left
else if (i > 0 && j < m && b[j] < a[i - 1])
max_index = i - 1;
// we have found the desired halves.
else
{
// this condition happens when we
// don't have any elements in the
// first half from a[] so we
// returning the last element in
// b[] from the first half.
if (i == 0)
median = b[j - 1];
// and this condition happens when
// we don't have any elements in the
// first half from b[] so we
// returning the last element in
// a[] from the first half.
else if (j == 0)
median = a[i - 1];
else
median = maximum(a[i - 1],
b[j - 1]);
break;
}
}
// calculating the median.
// If number of elements is odd
// there is one middle element.
if ((n + m) % 2 == 1)
return median;
// Elements from a[] in the
// second half is an empty set.
if (i == n)
return (median + b[j]) / 2.0;
// Elements from b[] in the
// second half is an empty set.
if (j == m)
return (median + a[i]) / 2.0;
return (median + minimum(a[i],
b[j])) / 2.0;
}
// Driver code
let n = a.length;
let m = b.length;
// we need to define the
// smaller array as the
// first parameter to
// make sure that the
// time complexity will
// be O(log(min(n,m)))
if (n < m)
document.write("The median is : " +
findMedianSortedArrays(n, m));
else
document.write("The median is : " +
findMedianSortedArrays(m, n));
// This code is contributed by unknown2108
</script>
The median is : 13.5
Otro enfoque: el mismo programa, pero devuelve la mediana que existe en la array combinada ((n + m) / 2 – 1 posición):
C++
// C++ code for finding median of the given two
// sorted arrays that exists in the merged array ((n+m) / 2 - 1 position)
#include<bits/stdc++.h>
using std::cout;
int maximum(int a, int b);
// Function to find median of given two sorted arrays
int findMedianSortedArrays(int *a, int n,
int *b, int m)
{
int min_index = 0, max_index = n, i, j;
while (min_index <= max_index)
{
i = (min_index + max_index) / 2;
j = ((n + m + 1) / 2) - i;
// if i = n, it means that Elements from a[] in
// the second half is an empty set. If j = 0, it
// means that Elements from b[] in the first half
// is an empty set. so it is necessary to check that,
// because we compare elements from these two groups.
// searching on right
if (i < n && j > 0 && b[j - 1] > a[i])
min_index = i + 1;
// if i = 0, it means that Elements from a[] in the
// first half is an empty set and if j = m, it means
// that Elements from b[] in the second half is an
// empty set. so it is necessary to check that,
// because we compare elements from these two groups.
// searching on left
else if (i > 0 && j < m && b[j] < a[i - 1])
max_index = i - 1;
// we have found the desired halves.
else
{
// this condition happens when we don't have
// any elements in the first half from a[] so
// we returning the last element in b[] from
// the first half.
if (i == 0)
return b[j - 1];
// and this condition happens when we don't have any
// elements in the first half from b[] so we
// returning the last element in a[] from the first half.
if (j == 0)
return a[i - 1];
else
return maximum(a[i - 1], b[j - 1]);
}
}
cout << "ERROR!!! " << "returning\n";
return 0;
}
// Function to find maximum
int maximum(int a, int b)
{
return a > b ? a : b;
}
// Driver code
int main()
{
int a[] = {900};
int b[] = { 10,13,14};
int n = sizeof(a) / sizeof(int);
int m = sizeof(b) / sizeof(int);
// we need to define the smaller array as the first
// parameter to make sure that the time complexity
// will be O(log(min(n,m)))
if (n < m)
cout << "The median is: "
<< findMedianSortedArrays(a, n, b, m);
else
cout << "The median is: "
<< findMedianSortedArrays(b, m, a, n);
return 0;
}
Java
// Java code for finding median of the
// given two sorted arrays that exists
// in the merged array ((n+m) / 2 -
// 1 position)
import java.io.*;
class GFG{
// Function to find maximum
static int maximum(int a, int b)
{
return a > b ? a : b;
}
// Function to find median
// of given two sorted arrays
static int findMedianSortedArrays(int []a, int n,
int []b, int m)
{
int min_index = 0,
max_index = n, i, j;
while (min_index <= max_index)
{
i = (min_index + max_index) / 2;
j = ((n + m + 1) / 2) - i;
// If i = n, it means that
// Elements from a[] in the
// second half is an empty
// set. If j = 0, it means
// that Elements from b[]
// in the first half is an
// empty set. so it is
// necessary to check that,
// because we compare elements
// from these two groups.
// searching on right
if (i < n && j > 0 &&
b[j - 1] > a[i])
min_index = i + 1;
// If i = 0, it means that
// Elements from a[] in the
// first half is an empty set
// and if j = m, it means that
// Elements from b[] in the
// second half is an empty set.
// so it is necessary to check
// that, because we compare
// elements from these two
// groups. searching on left
else if (i > 0 && j < m &&
b[j] < a[i - 1])
max_index = i - 1;
// We have found the
// desired halves.
else
{
// This condition happens
// when we don't have any
// elements in the first
// half from a[] so we
// returning the last
// element in b[] from
// the first half.
if (i == 0)
return b[j - 1];
// And this condition happens
// when we don't have any
// elements in the first half
// from b[] so we returning the
// last element in a[] from the
// first half.
if (j == 0)
return a[i - 1];
else
return maximum(a[i - 1],
b[j - 1]);
}
}
System.out.print("ERROR!!! " +
"returning\n");
return 0;
}
// Driver code
public static void main(String[] args)
{
int []a = {900};
int []b = {10, 13, 14};
int n = a.length;
int m = b.length;
// We need to define the smaller
// array as the first parameter
// to make sure that the time
// complexity will be O(log(min(n,m)))
if (n < m)
System.out.print("The median is: " +
findMedianSortedArrays(a, n,
b, m));
else
System.out.print("The median is: " +
findMedianSortedArrays(b, m,
a, n));
}
}
// This code is contributed by rag2127
Python3
# Python 3 code for finding median
# of the given two sorted arrays that
# exists in the merged array
# ((n+m) / 2 - 1 position)
# Function to find median of given
# two sorted arrays
def findMedianSortedArrays(a, n, b, m):
min_index = 0
max_index = n
while (min_index <= max_index):
i = (min_index + max_index) // 2
j = ((n + m + 1) // 2) - i
# if i = n, it means that Elements
# from a[] in the second half is
# an empty set. If j = 0, it means
# that Elements from b[] in the first
# half is an empty set. so it is necessary
# to check that, because we compare elements
# from these two groups. searching on right
if (i < n and j > 0 and b[j - 1] > a[i]):
min_index = i + 1
# if i = 0, it means that Elements from
# a[] in the first half is an empty set
# and if j = m, it means that Elements
# from b[] in the second half is an
# a[] in the first half is an empty set
# that, because we compare elements from
# these two groups. searching on left
elif (i > 0 and j < m and b[j] < a[i - 1]):
max_index = i - 1
# we have found the desired halves.
else:
# this condition happens when we don't have
# any elements in the first half from a[] so
# we returning the last element in b[] from
# the first half.
if (i == 0):
return b[j - 1]
# and this condition happens when we don't
# have any elements in the first half from
# b[] so we returning the last element in
# a[] from the first half.
if (j == 0):
return a[i - 1]
else:
return maximum(a[i - 1], b[j - 1])
print("ERROR!!! " , "returning\n")
return 0
# Function to find maximum
def maximum(a, b) :
return a if a > b else b
# Driver code
if __name__ == "__main__":
a = [900]
b = [10, 13, 14]
n = len(a)
m = len(b)
# we need to define the smaller array
# as the first parameter to make sure
# that the time complexity will be
# O(log(min(n,m)))
if (n < m):
print( "The median is: ",
findMedianSortedArrays(a, n, b, m))
else:
print( "The median is: ",
findMedianSortedArrays(b, m, a, n))
# This code is contributed
# by ChitraNayal
C#
// C# code for finding median
// of the given two sorted
// arrays that exists in the
// merged array ((n+m) / 2 -
// 1 position)
using System;
class GFG
{
// Function to find maximum
static int maximum(int a,
int b)
{
return a > b ? a : b;
}
// Function to find median
// of given two sorted arrays
static int findMedianSortedArrays(ref int []a, int n,
ref int []b, int m)
{
int min_index = 0,
max_index = n, i, j;
while (min_index <= max_index)
{
i = (min_index + max_index) / 2;
j = ((n + m + 1) / 2) - i;
// if i = n, it means that
// Elements from a[] in the
// second half is an empty
// set. If j = 0, it means
// that Elements from b[]
// in the first half is an
// empty set. so it is
// necessary to check that,
// because we compare elements
// from these two groups.
// searching on right
if (i < n && j > 0 &&
b[j - 1] > a[i])
min_index = i + 1;
// if i = 0, it means that
// Elements from a[] in the
// first half is an empty set
// and if j = m, it means that
// Elements from b[] in the
// second half is an empty set.
// so it is necessary to check
// that, because we compare
// elements from these two
// groups. searching on left
else if (i > 0 && j < m &&
b[j] < a[i - 1])
max_index = i - 1;
// we have found the
// desired halves.
else
{
// this condition happens
// when we don't have any
// elements in the first
// half from a[] so we
// returning the last
// element in b[] from
// the first half.
if (i == 0)
return b[j - 1];
// and this condition happens
// when we don't have any
// elements in the first half
// from b[] so we returning the
// last element in a[] from the
// first half.
if (j == 0)
return a[i - 1];
else
return maximum(a[i - 1],
b[j - 1]);
}
}
Console.Write ("ERROR!!! " +
"returning\n");
return 0;
}
// Driver code
static void Main()
{
int []a = new int[]{900};
int []b = new int[]{10, 13, 14};
int n = a.Length;
int m = b.Length;
// we need to define the smaller
// array as the first parameter
// to make sure that the time
// complexity will be O(log(min(n,m)))
if (n < m)
Console.Write ("The median is: " +
findMedianSortedArrays(ref a, n,
ref b, m));
else
Console.Write ("The median is: " +
findMedianSortedArrays(ref b, m,
ref a, n));
}
}
// This code is contributed by
// Manish Shaw(manishshaw1)
Javascript
<script>
// Javascript code for median with
// case of returning double
// value when even number of
// elements are present in
// both array combinely
let a=[900];
let b=[10, 13, 14];
// Function to find max
function maximum(a,b)
{
return a > b ? a : b;
}
// Function to find minimum
function minimum(a,b)
{
return a < b ? a : b;
}
// Function to find median
// of two sorted arrays
function findMedianSortedArrays(n,m)
{
let min_index = 0,
max_index = n, i = 0,
j = 0;
while (min_index <= max_index)
{
i = Math.floor((min_index + max_index) / 2);
j = Math.floor((n + m + 1) / 2) - i;
// if i = n, it means that Elements
// from a[] in the second half is an
// empty set. and if j = 0, it means
// that Elements from b[] in the first
// half is an empty set. so it is
// necessary to check that, because we
// compare elements from these two
// groups. Searching on right
if (i < n && j > 0 && b[j - 1] > a[i])
min_index = i + 1;
// if i = 0, it means that Elements
// from a[] in the first half is an
// empty set and if j = m, it means
// that Elements from b[] in the second
// half is an empty set. so it is
// necessary to check that, because
// we compare elements from these two
// groups. searching on left
else if (i > 0 && j < m && b[j] < a[i - 1])
max_index = i - 1;
// we have found the desired halves.
else
{
// this condition happens when we
// don't have any elements in the
// first half from a[] so we
// returning the last element in
// b[] from the first half.
if (i == 0)
return b[j - 1];
// and this condition happens when
// we don't have any elements in the
// first half from b[] so we
// returning the last element in
// a[] from the first half.
else if (j == 0)
return a[i - 1];
else
return maximum(a[i - 1],
b[j - 1]);
}
}
document.write("ERROR !! returning\n");
return 0;
}
// Driver code
let n = a.length;
let m = b.length;
// we need to define the
// smaller array as the
// first parameter to
// make sure that the
// time complexity will
// be O(log(min(n,m)))
if (n < m)
document.write("The median is : " +
findMedianSortedArrays(n, m));
else
document.write("The median is : " +
findMedianSortedArrays(m, n));
// This code is contributed by Aarti_Rathi
</script>
The median is: 13
Complejidad de tiempo: O (log (min (n, m))), donde n y m son los tamaños de la array ordenada dada
Publicación traducida automáticamente
Artículo escrito por Shlomi Elhaiani y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA