Método TOPSIS para la Toma de Decisiones de Criterios Múltiples (MCDM) – Part 1

La técnica de preferencia de orden por similitud con la solución ideal (TOPSIS) surgió en la década de 1980 como un método de toma de decisiones basado en criterios múltiples. TOPSIS elige la alternativa de menor distancia euclidiana a la solución ideal y mayor distancia a la solución ideal negativa. 

Para facilitar esta definición, supongamos que desea comprar un teléfono móvil, va a una tienda y analiza 5 teléfonos móviles en función de la RAM, la memoria, el tamaño de la pantalla, la batería y el precio. Por fin estás confundido después de ver tantos factores y no sabes cómo decidir qué teléfono móvil debes comprar. TOPSIS es una forma de asignar los rangos sobre la base de los pesos y el impacto de los factores dados. 

• Los pesos significan cuánto se debe tener en cuenta un factor determinado (peso predeterminado = 1 para todos los factores). como si quisiera que la RAM pesara más que otros factores, por lo que el peso de la RAM puede ser 2, mientras que otros pueden tener 1.
• Impacto significa que un factor dado tiene un impacto positivo o negativo. Por ejemplo, desea que la batería sea lo más grande posible pero que el precio del móvil sea lo más bajo posible, por lo que asignará un peso ‘+’ a la batería y un peso ‘-‘ al precio.

Este método se puede aplicar para clasificar los modelos de aprendizaje automático en función de varios factores como correlación, R^2, precisión, error cuadrático medio, etc. Ahora que hemos entendido qué es TOPSIS y dónde podemos aplicarlo. Veamos cuál es el procedimiento para implementar TOPSIS en un conjunto de datos determinado, que consta de varias filas (como varios teléfonos móviles) y varias columnas (como varios factores).

Ejemplo de conjunto de datos:

Los valores de datos dados para un factor en particular se deben considerar como unidades estándar. Siempre LabelEncode cualquier tipo de datos no numérico.

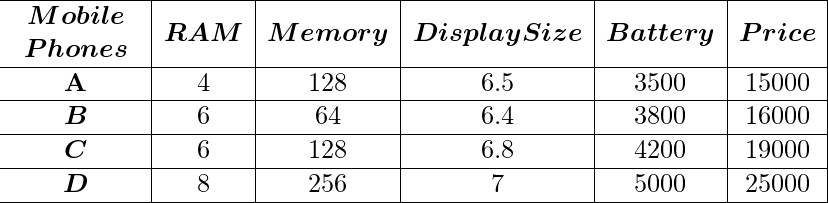
Procedimiento: 

Paso 1: Cálculo de la array normalizada y la array normalizada ponderada. Normalizamos cada valor haciéndolo: donde m es el número de filas en el conjunto de datos y n es el número de columnas. Yo varío a lo largo de las filas y j varía a lo largo de la columna.

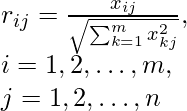
La array normalizada para los valores anteriores será:

Luego multiplicamos cada valor en una columna con el peso correspondiente dado.

# Arguments are dataset, number of columns, and weights of each column 
def Normalize(dataset, nCol, weights):
    for i in range(1, nCol):
        temp = 0
        # Calculating Root of Sum of squares of a particular column
        for j in range(len(dataset)):
            temp = temp + dataset.iloc[j, i]**2
        temp = temp**0.5
        # Weighted Normalizing a element
        for j in range(len(dataset)):
            dataset.iat[j, i] = (dataset.iloc[j, i] / temp)*weights[i-1]
    print(dataset)

Paso 2: Cálculo del valor ideal ideal y peor ideal y euclidiano para cada fila desde el peor ideal y el mejor valor ideal. Primero, encontraremos el mejor valor ideal y el peor ideal: Ahora aquí necesitamos ver el impacto, es decir, si es un impacto ‘+’ o ‘-‘. Si el impacto ‘+’ lo mejor ideal para una columna es el valor máximo en esa columna y lo peor ideal es el valor mínimo en esa columna, y viceversa para el impacto ‘-‘.

# Calculate ideal best and ideal worst
def Calc_Values(dataset, nCol, impact):
    p_sln = (dataset.max().values)[1:]
    n_sln = (dataset.min().values)[1:]
    for i in range(1, nCol):
        if impact[i-1] == '-':
            p_sln[i-1], n_sln[i-1] = n_sln[i-1], p_sln[i-1]
    return p_sln, n_sln

Ahora necesitamos calcular la distancia euclidiana para los elementos en todas las filas desde el mejor ideal y el peor ideal. Aquí d _iw es la peor distancia calculada de una i ^-ésima fila, donde ti _,j es el valor del elemento y t _w,j es el ideal . peor para esa columna. De manera similar, podemos encontrar d _ib , es decir, la mejor distancia calculada en una i ^-ésima fila.

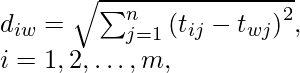
Ahora el conjunto de datos se verá así con la distancia positiva y negativa incluidas.

Paso 3: Cálculo de la puntuación y clasificación de Topsis. Ahora que tenemos distancia positiva y distancia negativa con nosotros, calculemos el puntaje de Topsis para cada fila en base a ellos.

Puntaje TOPSIS = d _iw / (d _ib + d _iw ) para cada fila

Ahora clasifique de acuerdo con la puntuación TOPSIS, es decir, cuanto mayor sea la puntuación, mejor será la clasificación.

Nuestro conjunto de datos se clasificará así:

¡El código para la última parte está aquí!

 # Calculating positive and negative values
 p_sln, n_sln = Calc_Values(temp_dataset, nCol, impact)

 # calculating topsis score
 score = [] # Topsis score
 pp = [] # distance positive
 nn = [] # distance negative
 
 
# Calculating distances and Topsis score for each row
 for i in range(len(temp_dataset)):
     temp_p, temp_n = 0, 0
     for j in range(1, nCol):
         temp_p = temp_p + (p_sln[j-1] - temp_dataset.iloc[i, j])**2
         temp_n = temp_n + (n_sln[j-1] - temp_dataset.iloc[i, j])**2
     temp_p, temp_n = temp_p**0.5, temp_n**0.5
     score.append(temp_n/(temp_p + temp_n))
     nn.append(temp_n)
     pp.append(temp_p)
    
 # Appending new columns in dataset   

 dataset['distance positive'] = pp
 dataset['distance negative'] = nn
 dataset['Topsis Score'] = score
 
 # calculating the rank according to topsis score
 dataset['Rank'] = (dataset['Topsis Score'].rank(method='max', ascending=False))
 dataset = dataset.astype({"Rank": int})

Puede encontrar el código fuente en mi Github Repo: Enlace