Métodos aglomerativos en aprendizaje automático

Antes de sumergirnos en los algoritmos aglomerativos, debemos comprender los diferentes conceptos en las técnicas de agrupamiento. Entonces, primero, mire el concepto de agrupamiento en aprendizaje automático:

La agrupación en clústeres es el amplio conjunto de técnicas para encontrar subgrupos o clústeres sobre la base de la caracterización de objetos dentro de un conjunto de datos, de modo que los objetos con grupos son similares pero diferentes del objeto de otros grupos. La pauta principal de la agrupación en clústeres es que los datos dentro de un clúster deben ser muy similares entre sí pero muy diferentes de los que están fuera de los clústeres. Existen diferentes tipos de técnicas de agrupamiento, como métodos de partición, métodos jerárquicos y métodos de partición.

Método	Características
Método de partición	Utiliza medio/medio para representar el centro del grupo Adopta un enfoque basado en la distancia para refinar los clústeres Encuentra grupos mutuamente excluyentes de forma esférica/casi esférica Efectivo para conjuntos de datos de pequeña a mediana edad
Método jerárquico	Crea una estructura similar a un árbol a través de la descomposición. Utiliza la distancia entre los puntos más cercanos/más lejanos en los clústeres vecinos para refinar El error no se puede corregir en niveles posteriores
Método basado en la densidad	Útil para identificar grupos de forma arbitraria Puede filtrar valores atípicos

En los métodos de particionamiento, existen 2 técnicas, a saber, k-means y k-mediods (algoritmo de particionamiento alrededor de mediods). Pero para aprender sobre los Métodos Aglomerativos, tenemos que discutir los métodos jerárquicos.

Métodos jerárquicos: los datos se agrupan en una estructura similar a un árbol. Hay dos algoritmos de agrupamiento principales en este método:
- A. Clustering divisivo: utiliza la estrategia de arriba hacia abajo, el punto de partida es el cluster más grande con todos los objetos en él y luego se divide recursivamente para formar clusters cada vez más pequeños. Termina cuando se logra la condición definida por el usuario o los grupos finales contienen solo un objeto.
- B. Clustering aglomerativo: utiliza un enfoque de abajo hacia arriba. Comienza con cada objeto formando su propio grupo y luego fusiona iterativamente los grupos según su similitud para formar grandes grupos. Termina ya sea
  - Cuando se logra cierta condición de agrupamiento impuesta por el usuario o
  - Todos los clústeres se fusionan en un solo clúster

Un dendograma, que es una estructura similar a un árbol, se usa para representar el agrupamiento jerárquico. Los objetos individuales están representados por Nodes hoja y los grupos están representados por Nodes raíz. En esta figura se muestra una representación del dendrograma :

Dendograma para agrupamiento

Ahora veremos las variantes de los métodos aglomerativos:

La distancia más cercana o enlace único es el método aglomerativo que utiliza la distancia entre los miembros más cercanos de los dos grupos. Ahora vamos a resolver un problema para entenderlo mejor:

Pregunta. Encuentre los clústeres utilizando una técnica de enlace único. Utilice la distancia euclidiana y dibuje el dendograma.

número de muestra	X	Y
P1	0.40	0.53
P2	0.22	0.38
P3	0.35	0.32
P4	0.26	0.19
P5	0.08	0.41
P6	0,45	0.30

Solución:

Paso 1: Calcular la array de distancia por: $d[(x,y)(a,b)] = \sqrt{(x-a)^2 + (y-b)^2}$

Entonces, tenemos que encontrar la distancia euclidiana entre todos y cada uno de los puntos, digamos que primero encontramos la distancia euclidiana entre P1 y P2

$d(P1,P2) = \sqrt{(0.4-0.22)^2 + (0.53-0.38)^2}$ = $\sqrt{(0.18)^2 + (0.15)^2} = \sqrt{0.0324+0.0225} = 0.23$

Entonces la MATRIZ DE DISTANCIA se verá así:

$\begin{pmatrix} & P1 & P2 & P3 & P4 & P5 & P6 \\ P1 & 0 \\ P2 & 0.23 & 0 \\ P3 & & & 0 \\ P4 & & & & 0 \\ P5 & & & & & 0 \\ P6 & & & & & & 0 \\ \end{pmatrix}$

Del mismo modo, encuentre la distancia euclidiana para cada punto. Pero hay un punto en el que centrarse: la diagonal de la array de distancia anterior es un punto especial para nosotros. La distancia por encima y por debajo de la diagonal será la misma. Por ejemplo: d(P2, P5) es equivalente a d(P5, P2) . Entonces encontraremos la distancia de la siguiente sección de la array.

$d(P1,P4) = \sqrt{(0.4-0.26)^2 + (0.53-0.19)^2} = \sqrt{(0.14)^2 + (0.34)^2} = \sqrt{0.0196+0.1156} = 0.3676 = 0.37$

$d(P1,P5) = \sqrt{(0.4-0.08)^2 + (0.53-0.41)^2} = \sqrt{(0.32)^2 + (0.12)^2} = \sqrt{0.1024+0.0144} = 0.3417 = 0.34$

$d(P1,P6) = \sqrt{(0.4-0.45)^2 + (0.53-0.30)^2} = \sqrt{(0.05)^2 + (0.23)^2} = \sqrt{0.0025+0.0529} = 0.2354 = 0.24$

$d(P2,P3) = \sqrt{(0.22-0.35)^2 + (0.38-0.32)^2} = \sqrt{(-0.13)^2 + (0.06)^2} = \sqrt{0.0169+0.0036} = 0.1432 = 0.14$

$d(P2,P4) = \sqrt{(0.22-0.26)^2 + (0.38-0.19)^2} = \sqrt{(-0.04)^2 + (0.19)^2} = \sqrt{0.0016+0.0361} = 0.1942 = 0.19$

$d(P2,P5) = \sqrt{(0.22-0.08)^2 + (0.38-0.41)^2} = \sqrt{(0.14)^2 + (-0.03)^2} = \sqrt{0.0196+0.0009} = 0.1432 = 0.14$

$d(P2,P3) = \sqrt{(0.22-0.35)^2 + (0.38-0.32)^2} = \sqrt{(-0.13)^2 + (0.06)^2} = \sqrt{0.0169+0.0036} = 0.0.1432 = 0.14$

$d(P2,P6) = \sqrt{(0.22-0.45)^2 + (0.38-0.30)^2} = \sqrt{(-0.23)^2 + (0.08)^2} = \sqrt{0.0529+0.0064} = 0.2435 = 0.24$

$d(P3,P4) = \sqrt{(0.35-0.26)^2 + (0.32-0.19)^2} = \sqrt{(0.03)^2 + (0.13)^2} = \sqrt{0.0009+0.0169} = 0.1334 = 0.13$

$d(P3,P5) = \sqrt{(0.35-0.08)^2 + (0.32-0.41)^2} = \sqrt{(0.27)^2 + (-0.09)^2} = \sqrt{0.0729+0.0081} = 0.2846 = 0.28$

$d(P3,P6) = \sqrt{(0.35-0.45)^2 + (0.32-0.30)^2} = \sqrt{(-0.1)^2 + (0.02)^2} = \sqrt{0.01+0.0004} = 0.10198 = 0.10$

$d(P4,P5) = \sqrt{(0.26-0.08)^2 + (0.19-0.41)^2} = \sqrt{(0.07)^2 + (-0.22)^2} = \sqrt{0.0049+0.0484} = 0.2309 = 0.23$

$d(P4,P6) = \sqrt{(0.26-0.45)^2 + (0.19-0.30)^2} = \sqrt{(-0.19)^2 + (-0.11)^2} = \sqrt{0.0361+0.0121} = 0.2195 = 0.22$

$d(P5,P6) = \sqrt{(0.08-0.45)^2 + (0.41-0.30)^2} = \sqrt{(-0.37)^2 + (0.11)^2} = \sqrt{0.1369+0.0121} = 0.3860 = 0.39$

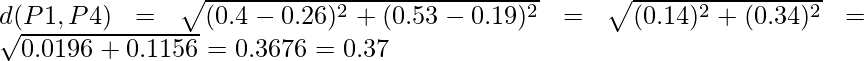
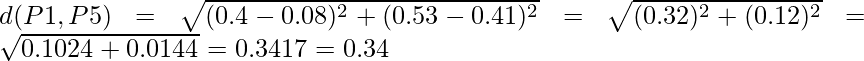
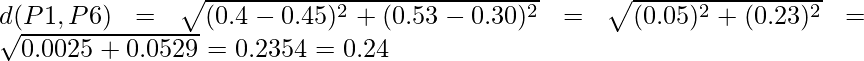
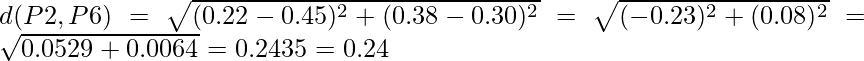
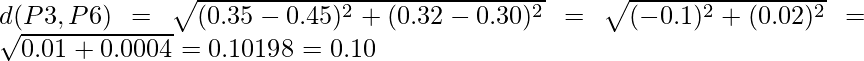
Por lo tanto, la Array de Distancia actualizada será:

$\begin{pmatrix} & P1 & P2 & P3 & P4 & P5 & P6 \\ P1 & 0 \\ P2 & 0.23 & 0 \\ P3 & 0.22 & 0.14 & 0 \\ P4 & 0.37 & 0.19 & 0.13 & 0 \\ P5 & 0.34 & 0.14 & 0.28 & 0.23 & 0 \\ P6 & 0.24 & 0.24 & 0.10 & 0.22 & 0.39 & 0 \\ \end{pmatrix}$

Paso 2: fusionar los dos miembros más cercanos de los dos grupos y encontrar el elemento mínimo en la array de distancia. Aquí el valor mínimo es 0.10 y por lo tanto combinamos P3 y P6 (ya que 0.10 vino en la fila P6 y la columna P3). Ahora, forme grupos de elementos correspondientes al valor mínimo y actualice la array de distancia. Para actualizar la array de distancia:

min ((P3,P6), P1) = min ((P3,P1), (P6,P1)) = min (0.22,0.24) = 0.22

min ((P3,P6), P2) = min ((P3,P2), (P6,P2)) = min (0.14,0.24) = 0.14

min ((P3,P6), P4) = min ((P3,P4), (P6,P4)) = min (0.13,0.22) = 0.13

min ((P3,P6), P5) = min ((P3,P5), (P6,P5)) = min (0.28,0.39) = 0.28

Ahora actualizaremos la array de distancia:

$\begin{pmatrix} & P1 & P2 & P3,P6 & P4 & P5 \\ P1 & 0 \\ P2 & 0.23 & 0 \\ P3,P6 & 0.22 & 0.14 & 0 \\ P4 & 0.37 & 0.19 & 0.13 & 0 \\ P5 & 0.34 & 0.14 & 0.28 & 0.23 & 0 \end{pmatrix}$

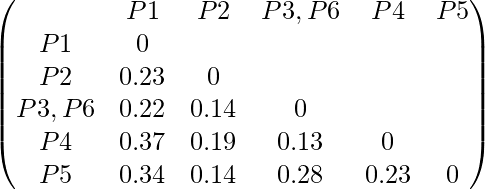
Ahora repetiremos el mismo proceso. Combine dos miembros más cercanos de los dos grupos y encuentre el elemento mínimo en la array de distancia. El valor mínimo es 0.13 y por lo tanto combinamos P3, P6 y P4. Ahora, forme los grupos de elementos correspondientes a los valores mínimos y actualice la array Distancia. Para encontrar, lo que tenemos que actualizar en array de distancia,

min (((P3,P6) P4), P1) = min (((P3,P6), P1), (P4,P1)) = min (0.22,0.37) = 0.22

min (((P3,P6), P4), P2) = min (((P3,P6), P2), (P4,P2)) = min (0.14,0.19) = 0.14

min (((P3,P6), P4), P5) = min (((P3,P6), P5), (P4,P5)) = min (0.28,0.23) = 0.23

Ahora actualizaremos la array de distancia:

$\begin{pmatrix} & P1 & P2 & P3,P6,P4 & P5 \\ P1 & 0 \\ P2 & 0.23 & 0 \\ P3,P6,P4 & 0.22 & 0.14 & 0 \\ P5 & 0.34 & 0.14 & 0.23 & 0 \end{pmatrix}$

Nuevamente repitiendo el mismo proceso: El valor mínimo es 0.14 y por lo tanto combinamos P2 y P5. Ahora, forme un grupo de elementos correspondientes al valor mínimo y actualice la array de distancia. Para actualizar la array de distancia:

mín ((P2,P5), P1) = mín ((P2,P1), (P5,P1)) = mín (0,23, 0,34) = 0,23

min ((P2,P5), (P3,P6,P4)) = min ((P3,P6,P4), (P3,P6,P4)) = min (0.14. 0.23) = 0.14

Actualizar array de distancia será:

$\begin{pmatrix} & P1 & P2,P5 & P3,P6,P4 \\ P1 & 0 \\ P2,P5 & 0.23 & 0 \\ P3,P6,P4 & 0.22 & 0.14 & 0 \\ \end{pmatrix}$

Nuevamente repitiendo el mismo proceso: El valor mínimo es 0.14 y por lo tanto combinamos P2,P5 y P3,P6,P4. Ahora, forme un grupo de elementos correspondientes al valor mínimo y actualice la array de distancia. Para actualizar la array de distancia:

min ((P2,P5,P3,P6,P4), P1) = min ((P2,P5), P1), ((P3,P6,P4), P1)) = min (0,23, 0,22) = 0,22

La array de distancia actualizada será:

$\begin{pmatrix} & P1 & P2,P5,P3,P6,P4 \\ P1 & 0 \\ P2,P5,P3,P6,P4 & 0.22 & 0 \end{pmatrix}$

Ahora que finalmente hemos llegado a la solución, el dendrograma para esas preguntas será el siguiente:

En este algoritmo, la distancia más lejana completa o el enlace completo es el método aglomerativo que utiliza la distancia entre los miembros que están más separados.

Pregunta. Para el conjunto de puntos dado, identifique los conglomerados utilizando el agrupamiento aglomerativo de enlace completo

Nº de muestra	X	Y
P1	1	1
P2	1.5	1.5
P3	5	5
P4	3	4
P5	4	4
P6	3	3.5

Solución.

Paso 1: Calcule la array de distancias por: $d[(x,y)(a,b)] = \sqrt{(x-a)^2 + (y-b)^2}$ Así que tenemos que encontrar la distancia euclidiana entre todos y cada uno de los puntos, digamos que primero encontramos la distancia euclidiana entre P1 y P2. (FÓRMULA PARA EL CÁLCULO DE LA DISTANCIA ES IGUAL A LA ANTERIOR)

Digamos que la array de distancia para algunos puntos es:

$\begin{pmatrix} & P1 & P2 & P3 & P4 & P5 & P6 \\ P1 & 0 \\ P2 & 0.71 & 0 \\ P3 & 5.66 & 4.95 & 0 \\ P4 & 3.6 & 2.92 & 2.24 & 0 \\ P5 & 4.24 & 3.53 & 1.41 & 1.0 & 0 \\ P6 & 3.20 & 2.5 & 2.5 & 0.5 & 1.12 & 0 \\ \end{pmatrix}$

Paso 2: fusionar los dos miembros más cercanos de los dos grupos y encontrar el elemento mínimo en la array de distancia. Entonces, el valor mínimo es 0.5 y por lo tanto combinamos P4 y P6. Para actualizar la array de distancia,

máx. (d(P4,P6), P1) = máx. (d(P4,P1), d(P6,P1)) = máx . (3,6, 3,2) = 3,6

máx. (d(P4,P6), P2) = máx. (d(P4,P2), d(P6,P2)) = máx. (2,92, 2,5) = 2,92

máx. (d(P4,P6), P3) = máx. (d(P4,P3), d(P6,P3)) = máx. (2,24, 2,5) = 2,5

máx. (d(P4,P6), P5) = máx. (d(P4,P5), d(P6,P5)) = máx. (1,0, 1,12) = 1,12

La array de distancia actualizada es:

$\begin{pmatrix} & P1 & P2 & P3 & P4,P6 & P5 \\ P1 & 0 \\ P2 & 0.71 & 0 \\ P3 & 5.66 & 4.95 & 0 \\ P4,P6 & 3.6 & 2.92 & 2.5 & 0 \\ P5 & 4.24 & 3.53 & 1.41 & 1.12 & 0 \\ \end{pmatrix}$

Nuevamente, fusionando los dos miembros más cercanos de los dos grupos y encontrando el elemento mínimo en la array de distancia. Obtenemos el valor mínimo como 0.71 y por lo tanto combinamos P1 y P2. Para actualizar la array de distancia,

máx (d(P1, P2), P3) = máx (d(P1, P3), d(P2, P3)) = máx (5,66, 4,95) = 5,66

máx (d(P1,P2), (P4,P6)) = máx (d(P1, P4, P6), d(P2, P4, P6)) = máx (3,6, 2,92) = 3,6

máx. (d(P1,P2), P5) = máx. (d(P1, P5), d(P2, P5)) = máx. (4,24, 3,53) = 4,24

La array de distancia actualizada es:

$\begin{pmatrix} & P1,P2 & P3 & P4,P6 & P5 \\ P1,P2 & 0 \\ P3 & 5.66 & 0 \\ P4,P6 & 3.6 & 2.5 & 0 \\ P5 & 4.24 & 1.41 & 1.12 & 0 \\ \end{pmatrix}$

Nuevamente, fusionando los dos miembros más cercanos de los dos grupos y encontrando el elemento mínimo en la array de distancia. Obtenemos el valor mínimo como 1.12 y por lo tanto combinamos P4, P6 y P5. Para actualizar la array de distancia,

máx. (d(P4,P6,P5), (P1,P2)) = máx. (d(P4,P6,P1,P2), d(P5,P1,P2)) = máx. (3,6, 4,24) = 4,24

máx. (d(P4,P6,P5), P3) = máx. (d(P4,P6,P3), d(P5, P3)) = máx. (2,5, 1,41) = 2,5

La array de distancia actualizada es:

$\begin{pmatrix} & P1,P2 & P3 & P4,P6,P5 \\ P1,P2 & 0 \\ P3 & 5.66 & 0 \\ P4,P6,P5 & 4.24 & 2.5 & 0 \\ \end{pmatrix}$

Nuevamente, fusionando los dos miembros más cercanos de los dos grupos y encontrando el elemento mínimo en la array de distancia. Obtenemos el valor mínimo como 2.5 y por lo tanto combinamos P4, P6, P5 y P3. para actualizar la array de distancia,

mín (d(P4,P6,P5,P3), (P1,P2)) = máx (d(P4,P6,P5,P1,P2), d(P3,P1,P2)) = mac (3,6, 5,66 ) = 5,66

La array de distancia actualizada es:

$\begin{pmatrix} & P1,P2 & P4,P6,P5,P3 \\ P1,P2 & 0 \\ P4,P6,P5,P3 & 5.66 & 0\\ \end{pmatrix}$

Ahora que finalmente hemos llegado a la solución, el dendrograma para esas preguntas será el siguiente:

La distancia promedio-promedio o el vínculo promedio es el método que implica observar las distancias entre todos los pares y promediar todas estas distancias. Esto también se denomina promedio de grupo de par universal.

Pregunta. Para los puntos dados en la pregunta anterior, identifique los clústeres utilizando el agrupamiento aglomerativo de enlaces promedio

Solución:

Primero tenemos que encontrar la array de distancia, ya que hemos elegido la misma pregunta, la array de distancia será la misma que la anterior:

Fusionar dos miembros más cercanos de los dos grupos y encontrar los elementos mínimos en la array de distancia. Obtenemos el valor mínimo como 0.5 y por lo tanto combinamos P4 y P6. Para actualizar la array de distancia:

promedio (d(P4,P6), P1) = promedio (d(P4,P1), d(P6,P1)) = promedio (3.6, 3.20) = 3.4

promedio (d(P4,P6), P2) = promedio (d(P4,P2), d(P6,P2)) = promedio (2.92, 2.5) = 2.71

promedio (d(P4,P6), P3) = promedio (d(P4,P3), d(P6,P3)) = promedio (2.24, 2.5) = 2.37

promedio (d(P4,P6), P5) = promedio (d(P4,P5), d(P6,P5)) = promedio (1.0, 1.12) = 1.06

La array de distancia actualizada es:

$\begin{pmatrix} & P1 & P2 & P3 & P4,P6 & P5 \\ P1 & 0 \\ P2 & 0.71 & 0 \\ P3 & 5.66 & 4.95 & 0 \\ P4,P6 & 3.4 & 2.71 & 2.37 & 0 \\ P5 & 4.24 & 3.53 & 1.41 & 1.06 & 0 \\ \end{pmatrix}$

Fusionar dos miembros más cercanos de los dos grupos y encontrar los elementos mínimos en la array de distancia. Obtenemos el valor mínimo como 0.71 y por lo tanto combinamos P1 y P2. Para actualizar la array de distancia:

promedio (d(P1,P2), P3) = promedio (d(P1,P3), d(P2,P3)) = promedio (5.66, 4.95) = 5.31

promedio (d(P1,P2), (P4,P6)) = promedio (d(P1,P4,P6), d(P2,P4,P6)) = promedio (3.2, 2.71) = 2.96

promedio (d(P1,P2), P5) = promedio (d(P1,P5), d(P2,P5)) = promedio (4.24, 3.53) = 3.89

La array de distancia actualizada es:

$\begin{pmatrix} & P1,P2 & P3 & P4,P6 & P5 \\ P1,P2 & 0 \\ P3 & 5.31 & 0 \\ P4,P6 & 2.96 & 2.5 & 0 \\ P5 & 3.89 & 1.41 & 1.12 & 0 \\ \end{pmatrix}$

Fusionar dos miembros más cercanos de los dos grupos y encontrar los elementos mínimos en la array de distancia. Obtenemos el valor mínimo como 1.12 y por lo tanto combinamos P4, P6 y P5. Para actualizar la array de distancia:

promedio (d(P4,P6,P5), (P1,P2)) = promedio (d(P4,P6,P1,P2), d(P5,P1,P2)) = promedio (2.96, 3.89) = 3.43

promedio (d(P4,P6,P5), P3) = promedio (d(P4,P6,P3), d(P5,P3)) = promedio (2.5, 1.41) = 1.96

La array de distancia actualizada es:

$\begin{pmatrix} & P1,P2 & P3 & P4,P6,P5 \\ P1,P2 & 0 \\ P3 & 5.66 & 0 \\ P4,P6,P5 & 3.43 & 1.96 & 0 \\ \end{pmatrix}$

Fusionar dos miembros más cercanos de los dos grupos y encontrar los elementos mínimos en la array de distancia. Obtenemos el valor mínimo como 1.96 y por lo tanto combinamos P4, P6, P5 y P3. Para actualizar la array de distancia:

promedio (d(P4,P6,P5,P3), (P1,P2)) = promedio (d(P4,P6,P5,P1,P2), d(P3,P1P2)) = promedio (3.43, 5.66) = 4.55

La array de distancia actualizada es:

$\begin{pmatrix} & P1,P2 & P4,P6,P5,P3 \\ P1,P2 & 0 \\ P4,P6,P5,P3 & 4.55 & 0 \\ \end{pmatrix}$

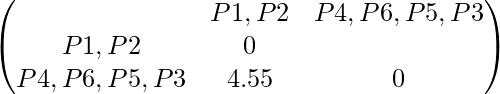
Entonces, el grupo final que se puede dibujar se muestra como:

Por lo tanto, hemos estudiado las tres variantes de los algoritmos aglomerativos.

Publicación traducida automáticamente

Artículo escrito por versatile1990 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta