Métodos de cálculo de la Desviación Estándar en series de distribución de frecuencia

Una medida científica de dispersión que se usa ampliamente en el análisis estadístico de un conjunto dado de datos se conoce como desviación estándar. Otro nombre para la desviación estándar es desviación cuadrática media . Se denota por un símbolo griego σ (sigma). Bajo este método, la desviación de los valores se toma de la media aritmética del conjunto de datos dado.

Según Spiegel, “La desviación estándar es la raíz cuadrada de la media aritmética de los cuadrados de todas las desviaciones. Las desviaciones se miden a partir de la media aritmética de los elementos”.

La desviación estándar se considera la mejor manera de determinar la dispersión de un conjunto de datos. Es porque la desviación estándar tiene en cuenta todos los valores de un conjunto de datos junto con sus signos algebraicos. Se puede calcular en tres series diferentes; a saber, serie de distribución individual, discreta y de frecuencia.

Métodos para calcular la desviación estándar en series de distribución de frecuencia

Método directo
Método abreviado
Método de desviación escalonada

1. Método Directo

En este método, la desviación estándar de una serie de datos se determina directamente a través de las desviaciones de la media aritmética de cada valor. Los pasos para calcular la desviación estándar de series discretas con el método directo son los siguientes:

En primer lugar, se determina la media aritmética de la serie o conjunto de datos dado. se denota por $\bar{X}$
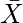
Ahora, las desviaciones de cada valor medio de los intervalos de clase o tamaño se toman de la media aritmética, es decir, x = m – $\bar{X}$
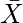
En el siguiente paso, las desviaciones determinadas se elevan al cuadrado y luego se multiplican por sus respectivas frecuencias, lo que da como resultado fx ²
El último paso es utilizar la fórmula del método directo para calcular la desviación estándar.

σ = $\sqrt{\frac{\sum{\\fx^{2}}}{N}}$

O

$\sqrt{\frac{\sum f(X - \bar{X})^{2}}{N}}$

Ejemplo: Calcular la desviación estándar de la siguiente serie por Método Directo.

Intervalo de clases	0-10	10-20	20-30	30-40	40-50
Frecuencia	2	7	10	5	3

Solución:

Intervalo de clases Valor medio (m) Frecuencia (f) FM $x = m - \bar{X}$
$\bar{X} = 32.5$ x2 ^_ efecto ²

0 – 10 5 2 10 -20 400 800

10 – 20 15 7 105 -10 100 700

20 – 30 25 10 250 0 0 0

30 – 40 35 5 175 10 100 500

40 – 50 45 3 135 20 400 1200

norte = 27 ∑fm = 675 ∑fx2 ⁼ 3200

σ = $\sqrt{\frac{\sum{\\fx^{2}}}{N}}$

= $\sqrt{\frac{3200}{27}}$

= $\sqrt{118.52}$

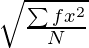
= 10,89

Desviación Estándar = 10.89

Intervalo de clases	Valor medio (m)	Frecuencia (f)	FM	$x = m - \bar{X}$ $\bar{X} = 32.5$	x2 ^_	efecto ²
0 – 10	5	2	10	-20	400	800
10 – 20	15	7	105	-10	100	700
20 – 30	25	10	250	0	0	0
30 – 40	35	5	175	10	100	500
40 – 50	45	3	135	20	400	1200
		norte = 27	∑fm = 675			∑fx2 ⁼ 3200

2. Método abreviado

En este método, la desviación estándar de una serie de datos se determina obteniendo desviaciones de los valores medios de los intervalos de clase de un conjunto de datos. La desviación de los valores medios se toma de la media aritmética del conjunto de datos. Los pasos para calcular la desviación estándar de la serie de distribución de frecuencia con el método abreviado son los siguientes:

En primer lugar, se asume un valor a partir de los valores medios del conjunto de datos dado y luego se toman las desviaciones del valor asumido a partir de los valores medios. La desviación se denota por d (d = m – A)
Ahora, las frecuencias del conjunto de datos se multiplican por sus respectivas desviaciones y se denotan por fd.
En el siguiente paso, la fd determinada en el paso anterior se multiplica por las desviaciones (d).
El último paso es calcular la desviación estándar de la serie de distribución de frecuencia usando la fórmula.

σ = $\sqrt{{\frac{\sum{\\fd^{2}}}{N}}-({\frac{\sum{fd}}{N}})^2}$

Ejemplo: Calcular la desviación estándar de la siguiente serie por el método de atajo.

Intervalo de clases	0-10	10-20	20-30	30-40	40-50	50-60
Frecuencia	15	17	19	27	19	12

Solución:

Intervalo de clases Valor medio (m) Frecuencia (f)
re = metro – A (A = 35)
f.d. fd ²

0-10 5 15 -30 -450 13500

10-20 15 17 -20 -340 6800

20-30 25 19 -10 -190 mil novecientos

30-40 35 (A) 27 0 0 0

40-50 45 19 10 190 mil novecientos

50-60 55 12 20 240 4800

norte = 109 ∑fd = -550 ∑fd ² = 28900

σ = $\sqrt{{\frac{\sum{\\fd^{2}}}{N}}-({\frac{\sum{fd}}{N}})^2}$

= $\sqrt{{\frac{28900}{109}}-({\frac{-550}{109}})^2}$

= $\sqrt{265.13-(-5.04)^2}$

= $\sqrt{265.13 - 25.40}$

= $\sqrt{239.76}$

= 15,48

Desviación Estándar = 15.48

Intervalo de clases	Valor medio (m)	Frecuencia (f)	re = metro – A (A = 35)	f.d.	fd ²
0-10	5	15	-30	-450	13500
10-20	15	17	-20	-340	6800
20-30	25	19	-10	-190	mil novecientos
30-40	35 (A)	27	0	0	0
40-50	45	19	10	190	mil novecientos
50-60	55	12	20	240	4800
		norte = 109		∑fd = -550	∑fd ² = 28900

3. Método de paso-desviación

En este método, la desviación estándar de una serie de datos se determina tomando en consideración un factor común de los intervalos de clase. Es el método más popular para determinar la desviación estándar.
Los pasos para calcular la desviación estándar de una serie de distribución de frecuencias por el método de paso-desviación son los siguientes:

En primer lugar, se asume un valor a partir de los valores medios del conjunto de datos dado, y luego se toman las desviaciones del valor asumido a partir de los valores medios. La desviación se denota por d (d = m – A).
El siguiente paso es dividir las desviaciones por su factor común, denotado por d’ (d’ = $\frac{d}{C}$ ).
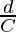Ahora, d’ se multiplica por sus respectivas frecuencias para obtener fd’
En el siguiente paso, fd’ se multiplica por d’ para obtener fd’ ²
El último paso es calcular la desviación estándar de la serie de distribución de frecuencia usando la fórmula.

$σ = \sqrt{{\frac{\sum{\\fd'^{2}}}{N}}-({\frac{\sum{fd'}}{N}})^2}\times C$

Ejemplo: Calcule la desviación estándar de la siguiente serie por el método de desviación escalonada.

Intervalo de clases	0-10	10-20	20-30	30-40	40-50	50-60	60-70	70-80
Frecuencia	5	10	20	40	30	20	10	5

Solución:

Intervalo de clases Valor medio (m) Frecuencia (f)
re = metro – A (A=45)
fd’ fd’2 ^_

0-10 5 5 -40 -4 -20 80

10-20 15 10 -30 -3 -30 90

20-30 25 20 -20 -2 -40 80

30-40 35 40 -10 -1 -40 40

40-50 45 (A) 30 0 0 0 0

50-60 55 20 10 1 20 20

60-70 sesenta y cinco 10 20 2 20 40

70-80 75 5 30 3 15 45

norte = 140 ∑fd’ = -75 ∑fd’2 ⁼ 375

σ = $\sqrt{{\frac{\sum{\\fd'^{2}}}{N}}-({\frac{\sum{fd'}}{N}})^2}\times C$

= ${\sqrt{\frac{375}{140} - ({\frac{-75}{140}})^2}}\times 10$

= ${\sqrt{2.678 - (-0.535)^2}}\times 10$

= ${\sqrt{2.678 - 0.286}}\times 10$

= $\sqrt{2.392}\times 10$

= $1.546\times10$

= 15,46

Desviación Estándar = 15.46

Intervalo de clases	Valor medio (m)	Frecuencia (f)	re = metro – A (A=45)	fd’	fd’2 ^_
0-10	5	5	-40	-4	-20	80
10-20	15	10	-30	-3	-30	90
20-30	25	20	-20	-2	-40	80
30-40	35	40	-10	-1	-40	40
40-50	45 (A)	30	0	0	0	0
50-60	55	20	10	1	20	20
60-70	sesenta y cinco	10	20	2	20	40
70-80	75	5	30	3	15	45
		norte = 140			∑fd’ = -75	∑fd’2 ⁼ 375