Métodos de clase matemática en Java con ejemplos | conjunto 2

Posted on by Rudeus Greyrat

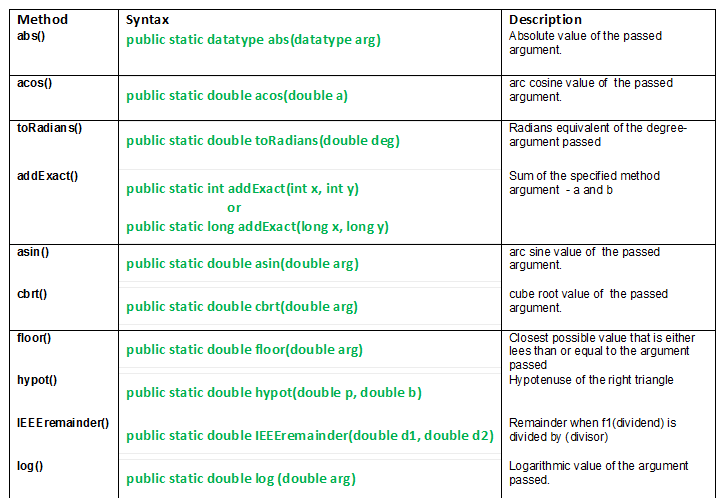
clase java.math y sus métodos | Establecer 1 métodos de clase java.math discutidos en este artículo:

java.math class methods

  1. abs() : el método java.math.abs() devuelve el valor absoluto de cualquier tipo de argumento pasado. Este método puede manejar todos los tipos de datos.
      Caso especial :

    • El resultado es cero positivo, si el argumento es cero positivo o cero negativo.
    • El resultado es infinito positivo, si el argumento es infinito.
    • El resultado es NaN, si el argumento pasado es NaN.

    Sintaxis:

    public static datatype abs(datatype arg)
Parameters:
arg - the argument whose absolute value we need
Returns:
absolute value of the passed argument.
  2. acos() : el método java.math.acos() devuelve el valor del arco coseno del argumento pasado.
    el arco coseno es el coseno inverso del argumento pasado.
    acos(arg) = cos -1 of arg
    Caso especial: el resultado es NaN, si el argumento es NaN o su valor absoluto es mayor que 1.
    Sintaxis: 
    public static double acos(double a)
Parameters:
a - the argument whose arc cosine value we need.
    argument is taken as radian    
Returns:
arc cosine value of the argument.
  3. toRadians() : el método java.math.toRadians(doble grado) convierte el argumento (grado) en radianes.
    Punto especial: la clase de matemáticas generalmente toma radianes como entrada, lo cual es muy diferente en las aplicaciones de la vida real, ya que los ángulos generalmente se representan en grados.
    Sintaxis: 
    public static double toRadians(double deg)
Parameters:
deg - degree angle needs to be in radian.
Returns:
radians equivalent of the degree-argument passed.

    4. ¿Qué es el argumento NaN?
    Una constante que contiene un valor Not-a-Number (NaN) de tipo double. Es equivalente al valor devuelto por Double.longBitsToDouble(0x7ff8000000000000L).

    Código Java que explica el método abs(), acos(), toRadians() en la clase de matemáticas.

    // Java program explaining Math class methods
    // abs(), acos(), toRadians()
    import java.math.*;
    public class NewClass
    {
      
        public static void main(String[] args)
        {
            // Declaring the variables
            int Vali = -1;
            float Valf = .5f;
      
            // Printing the values
            System.out.println("Initial value of int  : "+Vali);
            System.out.println("Initial value of int  : "+Valf);
      
      
            // Use of .abs() method to get the absoluteValue
            int Absi = Math.abs(Vali);
            float Absf = Math.abs(Valf);
      
            System.out.println("Absolute value of int : "+Absi);
            System.out.println("Absolute value of int : "+Absf);
            System.out.println("");
      
            // Use of acos() method
            // Value greater than 1, so passing NaN
            double Acosi = Math.acos(60);
            System.out.println("acos value of Acosi : "+Acosi);
            double x = Math.PI;
      
            // Use of toRadian() method
            x = Math.toRadians(x);
            double Acosj = Math.acos(x);
            System.out.println("acos value of Acosj : "+Acosj);
              
        }
    }

    Producción:

    Initial value of int  : -1
Initial value of int  : 0.5
Absolute value of int : 1
Absolute value of int : 0.5

acos value of Acosi : NaN
acos value of Acosj : 1.5159376794536454
  4. addExact() : el método java.math.addExact(int a, int b) devuelve la suma de los argumentos pasados.
    Punto especial: si Result desborda un int o long (según el argumento pasado), el método lanza ArithmeticException.
    Sintaxis: 
    public static int addExact(int x, int y)
                or
public static long addExact(long x, long y)
Parameters:
a - first value
b - second value
Returns:
Sum of the specified method arguments - a and b.
  5. asin() : el método java.math.asin() devuelve el valor del arco seno del argumento del método pasado. El ángulo devuelto está en el rango -pi/2 a pi/2.
    arco seno es el seno inverso del argumento pasado.
    asin(arg) = seno -1 de arg
    Caso especial:
    • El resultado es NaN, si el argumento es NaN o su valor absoluto es mayor que 1.
    • El resultado es un cero, si el argumento es cero.

    Sintaxis:

    public static double asin(double arg)
Parameters:
arg - argument passed. 
Returns:
arc sine of the argument passed.
  6. cbrt() : el método java.math.cbrt() devuelve la raíz cúbica del argumento pasado.
    Punto especial:
    • El resultado es NaN, si el argumento es NaN.
    • El resultado es un infinito con el mismo signo que el argumento, si el argumento es infinito.
    • El resultado es un cero, si el argumento es cero.

    Sintaxis:

    public static double cbrt(double arg)
Parameters:
arg - argument passed. 
Returns:
cube root of the argument passed

    7. Código Java que explica el método addExact(), asin(), cbrt() en la clase Math.

    // Java program explaining Math class methods
    // addExact(), asin(), cbrt()
    import java.math.*;
    public class NewClass
    {
      
        public static void main(String[] args)
        {
            int a = 1, b = 8;
      
            // get the result of addExact method
            int radd = Math.addExact(a,b);
            System.out.println("Using addExact() : "+radd);
            System.out.println("");
      
            // Use of acos() method
            // Value greater than 1, so passing NaN
            double Asini = Math.asin(radd);
            System.out.println("asin value of Asini : "+Asini);
            double x = Math.PI;
      
            // Use of toRadian() method
            x = Math.toRadians(x);
            double Asinj = Math.asin(x);
            System.out.println("asin value of Asinj : "+Asinj);
            System.out.println("");
      
            // Use of cbrt() method
            double cbrtval = Math.cbrt(216);
            System.out.println("cube root : "+cbrtval);
      
        }
    }

    Producción:

    Using addExact() : 9

acos value of Asini : NaN
acos value of Asinj : 0.054858647341251204

cube root : 6.0
  7. floor() : el método java.math.floor() devuelve el valor mínimo de un argumento, es decir, el valor entero más cercano que es menor o igual que el argumento pasado.
    Por ejemplo: 101,23 tiene un valor mínimo = 101.
    Punto importante: se obtiene el mismo argumento si se pasa un argumento NaN o infinito. 
    Syntax:
public static double floor(double arg)
Parameters:
arg - the argument whose floor value we need
Returns:closest possible value that is either less than 
                or equal to the argument passed
  8. hypot() : el método java.math.hypot(doble p, doble b) devuelve la hipotenusa de un triángulo rectángulo al pasar la base del triángulo y la perpendicular como argumentos.
    hipotenusa = [perpendicular 2 + base 2 ] 1/2

    Punto importante :

    • Si cualquiera de los argumentos es infinito, entonces el resultado es infinito positivo.
    • Si cualquiera de los argumentos es NaN y ninguno de los dos es infinito, entonces el resultado es NaN.
    Syntax:
public static double hypot(double p, double b)
Parameters:
p - perpendicular of the right triangle
b - base of the right triangle
Returns:
hypotenuse of the right triangle
  9. IEEEremainder() : el método java.math.IEEERemainder(doble d1, doble d2) devuelve el valor restante aplicando la operación restante en dos argumentos con el estándar IEEE 754.
    Valor restante = d1 – d2 * n
    donde,
    n = valor exacto más cercano de d1/d2 
    Syntax:
public static double IEEEremainder(double d1,double d2)
Parameters:
d1 - dividend 
d2 - divisor
Returns:
remainder when f1(dividend) is divided by(divisor)
  10. log() : el método java.math.log() devuelve el valor logarítmico del argumento pasado. 
    Syntax:
public static double log(double arg)
Parameters:
arg - argument passed. 
Returns:
logarithmic value of the argument passed.

    11. Código Java que explica el método floor(), hypot(), IEEEremainder(), log() en la clase Math.

    // Java program explaining MATH class methods
    // floor(), hypot(), IEEEremainder(), log()
    import java.lang.*;
    public class NewClass
    {
      
        public static void main(String[] args)
        {
            // Use of floor method
            double f1 = 30.56, f2 = -56.34;
            f1 =Math.floor(f1);
            System.out.println("Floor value of f1 : "+f1);
      
            f2 =Math.floor(f2);
            System.out.println("Floor value of f2 : "+f2);
            System.out.println("");
      
            // Use of hypot() method
            double p = 12, b = -5;
            double h = Math.hypot(p, b);
            System.out.println("Hypotenuse : "+h);
            System.out.println("");
      
            // Use of IEEEremainder() method
            double d1 = 105, d2 = 2;
            double r = Math.IEEEremainder(d1,d2);
            System.out.println("Remainder : "+r);
            System.out.println("");
              
            // Use of log() method
            double l = 10;
            l = Math.log(l);
            System.out.println("Log value of 10 : "+l);
              
        }
    }

    Producción:

    Floor value of f1 : 30.0
Floor value of f2 : -57.0

Hypotenuse : 13.0

Remainder : 1.0

Log value of 10 : 2.302585092994046

    clase java.math y sus métodos | conjunto 3

    Este artículo es una contribución de Mohit Gupta . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.

    Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *