Minimización de DFA

La minimización de DFA significa convertir un DFA determinado en su DFA equivalente con un número mínimo de estados. 

Minimización de DFA 
Supongamos que hay un DFA D < Q, Σ, q0, δ, F > que reconoce un idioma L. Entonces se puede construir el DFA minimizado < Q’, Σ, q0, δ’, F’ > para el idioma L como: 
Paso 1: Dividiremos Q (conjunto de estados) en dos conjuntos. Un conjunto contendrá todos los estados finales y otro conjunto contendrá estados no finales. Esta partición se llama P ₀ . 
Paso 2: Inicialice k = 1 
Paso 3: Encuentre P _k dividiendo los diferentes conjuntos de P _k-1 . En cada conjunto de P _k-1 , tomaremos todos los pares de estados posibles. Si dos estados de un conjunto son distinguibles, dividiremos los conjuntos en diferentes conjuntos en P _k . 
Paso 4:Detener cuando P _k = P _k-1 (Sin cambios en la partición) 
Paso 5: Todos los estados de un conjunto se fusionan en uno. El número de estados en DFA minimizado será igual al número. de conjuntos en P _k . 

¿Cómo encontrar si dos estados en la partición _Pk son distinguibles?  
Dos estados (qi, qj) se distinguen en la partición _Pk si para cualquier símbolo de entrada a, δ (qi, a) y δ (qj, a) están en diferentes conjuntos en la partición _Pk-1 . 
Ejemplo 
Considere el siguiente DFA que se muestra en la figura. 
 

Paso 1. P0 tendrá dos conjuntos de estados. Un conjunto contendrá q1, q2, q4 que son estados finales de DFA y otro conjunto contendrá los estados restantes. Entonces P0 = { { q1, q2, q4 }, { q0, q3, q5 } }. 
Paso 2. Para calcular P1, comprobaremos si los conjuntos de la partición P0 se pueden particionar o no: 

i) Para el conjunto { q1, q2, q4 } : 
δ ( q1, 0 ) = δ ( q2, 0 ) = q2 y δ ( q1, 1 ) = δ ( q2, 1 ) = q5, Entonces q1 y q2 no son distinguible. 
De manera similar, δ ( q1, 0 ) = δ ( q4, 0 ) = q2 y δ ( q1, 1 ) = δ ( q4, 1 ) = q5, por lo que q1 y q4 no son distinguibles. 
Dado que q1 y q2 no son distinguibles y q1 y q4 tampoco son distinguibles, entonces q2 y q4 no son distinguibles. Entonces, el conjunto { q1, q2, q4 } no se dividirá en P1. 

ii) Para el conjunto { q0, q3, q5 } : 
δ ( q0, 0 ) = q3 y δ ( q3, 0 ) = q0 
δ ( q0, 1) = q1 y δ( q3, 1 ) = q4 
Movimientos de q0 y q3 en el símbolo de entrada 0 son q3 y q0 respectivamente, que están en el mismo conjunto en la partición P0. De manera similar, los movimientos de q0 y q3 en el símbolo de entrada 1 son q1 y q4, que están en el mismo conjunto en la partición P0. Entonces, q0 y q3 no son distinguibles. 

δ ( q0, 0 ) = q3 y δ ( q5, 0 ) = q5 y δ ( q0, 1 ) = q1 y δ ( q5, 1 ) = q5 Los 
movimientos de q0 y q5 en el símbolo de entrada 1 son q1 y q5 respectivamente, que están en un conjunto diferente en la partición P0. Entonces, q0 y q5 son distinguibles. Entonces, el conjunto { q0, q3, q5 } se dividirá en { q0, q3 } y { q5 }. Entonces, 
P1 = { { q1, q2, q4 }, { q0, q3}, { q5 } } 

Para calcular P2, comprobaremos si los conjuntos de la partición P1 se pueden particionar o no: 
iii) Para el conjunto { q1, q2, q4 } : 
δ ( q1, 0 ) = δ ( q2, 0 ) = q2 y δ ( q1, 1 ) = δ ( q2, 1 ) = q5, Entonces q1 y q2 no son distinguibles. 
De manera similar, δ ( q1, 0 ) = δ ( q4, 0 ) = q2 y δ ( q1, 1 ) = δ ( q4, 1 ) = q5, por lo que q1 y q4 no son distinguibles. 
Dado que q1 y q2 no son distinguibles y q1 y q4 tampoco son distinguibles, entonces q2 y q4 no son distinguibles. Entonces, el conjunto { q1, q2, q4 } no se dividirá en P2. 

iv)Para el conjunto { q0, q3 } : 
δ ( q0, 0 ) = q3 y δ ( q3, 0 ) = q0 
δ ( q0, 1 ) = q1 y δ ( q3, 1 ) = q4 
Movimientos de q0 y q3 en el símbolo de entrada 0 son q3 y q0 respectivamente, que están en el mismo conjunto en la partición P1. De manera similar, los movimientos de q0 y q3 en el símbolo de entrada 1 son q1 y q4, que están en el mismo conjunto en la partición P1. Entonces, q0 y q3 no son distinguibles. 

v) Para el conjunto { q5 }: 
dado que solo tenemos un estado en este conjunto, no se puede particionar más. Entonces, 
P2 = { { q1, q2, q4 }, { q0, q3 }, { q5 } } 
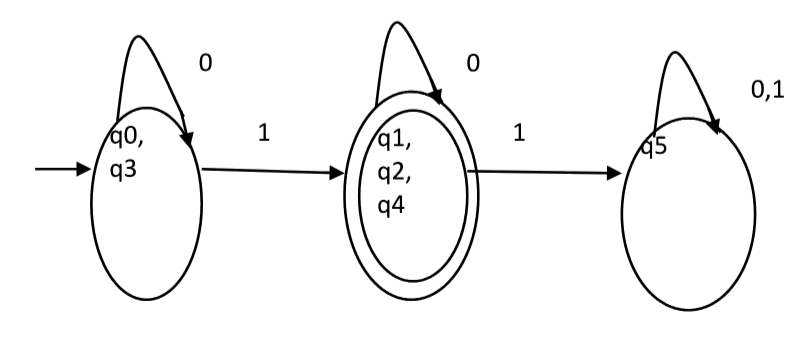
Ya que, P1=P2. Entonces, esta es la partición final. La partición P2 significa que los estados q1, q2 y q4 se fusionan en uno. De manera similar, q0 y q3 se fusionan en uno. El DFA minimizado correspondiente al DFA de la Figura 1 se muestra en la Figura 2 como: 
 

  

Pregunta: Considere el DFA dado. ¿Cuál de las siguientes es falsa? 
1. El complemento de L(A) no tiene contexto. 
2. L(A) = L ( ( 11 * 0 + 0 ) ( 0 + 1 )* 0* 1* ) 
3. Para el lenguaje aceptado por A, A es el DFA mínimo. 
4. A acepta todas las strings superiores a { 0, 1 } de al menos dos longitudes. 
 

A. 1 y 3 únicamente 
B. 2 y 4 únicamente 
C. 2 y 3 únicamente 
D. 3 y 4 únicamente 

Solución: la declaración 4 dice que aceptará todas las strings de al menos 2 de longitud. Pero acepta 0, que tiene una longitud de 1. Por lo tanto, 4 es falso. 
La declaración 3 dice que el DFA es mínimo. Verificaremos usando el algoritmo discutido anteriormente. 
P0 = { { q2 }, { q0, q1 } } 
P1 = { q2 }, { q0, q1 } }. Como P0 = P1, P1 es el DFA final. q0 y q1 se pueden fusionar. Entonces, el DFA mínimo tendrá dos estados. Por lo tanto, la afirmación 3 también es falsa. 
Entonces la opción correcta es (D). 

Este artículo ha sido aportado por Sonal Tuteja. 

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.