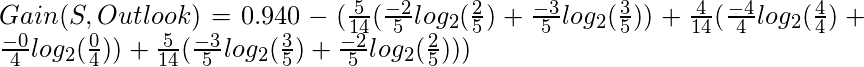ML | Clasificador de árbol adicional para la selección de funciones

Prerrequisitos: Clasificador de árboles de decisión

El clasificador de árboles extremadamente aleatorios (clasificador de árboles extra) es un tipo de técnica de aprendizaje de conjunto que agrega los resultados de múltiples árboles de decisión descorrelacionados recopilados en un «bosque» para generar su resultado de clasificación. En concepto, es muy similar a un Random Forest Classifier y solo se diferencia de él en la forma de construcción de los árboles de decisión en el bosque.

Cada árbol de decisión en el bosque de árboles adicionales se construye a partir de la muestra de entrenamiento original. Luego, en cada Node de prueba, a cada árbol se le proporciona una muestra aleatoria de k características del conjunto de características del cual cada árbol de decisión debe seleccionar la mejor característica para dividir los datos en función de algunos criterios matemáticos (normalmente, el índice de Gini). Esta muestra aleatoria de características conduce a la creación de múltiples árboles de decisión no correlacionados.

Para realizar la selección de características usando la estructura de bosque anterior, durante la construcción del bosque, para cada característica, la reducción total normalizada en los criterios matemáticos utilizados en la decisión de característica de división (Índice de Gini si el Índice de Gini se usa en la construcción de el bosque) se calcula. Este valor se denomina Importancia de Gini de la función. Para realizar la selección de funciones, cada función se ordena en orden descendente de acuerdo con la importancia de Gini de cada función y el usuario selecciona las k principales funciones de acuerdo con su elección.

Considere los siguientes datos:-

Construyamos un bosque de árboles extra hipotético para los datos anteriores con cinco árboles de decisión y el valor de k que decide que el número de características en una muestra aleatoria de características sea dos . Aquí el criterio de decisión utilizado será la Ganancia de Información. Primero, calculamos la entropía de los datos. Tenga en cuenta que la fórmula para calcular la entropía es: –

$Entropy(S) = \sum _{i=1}^{c} -p_{i}log_{2}(p_{i})$

donde c es el número de etiquetas de clase únicas y $p_{i}$ la proporción de filas con etiqueta de salida es i.

Por lo tanto, para los datos dados, la entropía es: –

$Entropy(S) = -\frac{9}{14}log(\frac{9}{14})-\frac{5}{14}log(\frac{5}{14})$

$\Rightarrow Entropy(S) = 0.940$

Deje que los árboles de decisión se construyan de tal manera que: –

1st Decision Tree obtiene datos con las características Outlook y Temperature:

Tenga en cuenta que la fórmula para la ganancia de información es: –

$Gain(S, A) = Entropy(S) - \sum _{v\epsilon Values(A)} \frac{|S_{v}|}{|S|}Entropy(S_{v})$

De este modo,

Similarmente:

2nd Decision Tree obtiene datos con las funciones Temperatura y Viento:

Usando las fórmulas dadas anteriormente: –

strong>3rd Decision Tree obtiene datos con las funciones Outlook y Humidity:

4th Decision Tree obtiene datos con las funciones Temperatura y Humedad:

5th Decision Tree obtiene datos con las características Viento y Humedad:

Cálculo de la ganancia de información total para cada característica: –


Total Info Gain for Outlook     =     0.246+0.246   = 0.492

Total Info Gain for Temperature = 0.029+0.029+0.029 = 0.087

Total Info Gain for Humidity    = 0.151+0.151+0.151 = 0.453

Total Info Gain for Wind        =     0.048+0.048   = 0.096

Por lo tanto, la variable más importante para determinar la etiqueta de salida de acuerdo con el Bosque de árboles extra construido anteriormente es la característica «Perspectiva».

El código dado a continuación demostrará cómo hacer una selección de características usando Clasificadores de árboles adicionales.

Paso 1: Importación de las bibliotecas requeridas

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import ExtraTreesClassifier

Paso 2: carga y limpieza de datos

# Changing the working location to the location of the file
cd C:\Users\Dev\Desktop\Kaggle
  
# Loading the data
df = pd.read_csv('data.csv')
  
# Separating the dependent and independent variables
y = df['Play Tennis']
X = df.drop('Play Tennis', axis = 1)
  
X.head()

Paso 3: construir el bosque de árboles adicionales y calcular la importancia de las características individuales

# Building the model
extra_tree_forest = ExtraTreesClassifier(n_estimators = 5,
                                        criterion ='entropy', max_features = 2)
  
# Training the model
extra_tree_forest.fit(X, y)
  
# Computing the importance of each feature
feature_importance = extra_tree_forest.feature_importances_
  
# Normalizing the individual importances
feature_importance_normalized = np.std([tree.feature_importances_ for tree in 
                                        extra_tree_forest.estimators_],
                                        axis = 0)

Paso 4: Visualización y comparación de los resultados

# Plotting a Bar Graph to compare the models
plt.bar(X.columns, feature_importance_normalized)
plt.xlabel('Feature Labels')
plt.ylabel('Feature Importances')
plt.title('Comparison of different Feature Importances')
plt.show()

Por lo tanto, el resultado anterior valida nuestra teoría sobre la selección de características utilizando el clasificador de árboles adicionales. La importancia de las características puede tener valores diferentes debido a la naturaleza aleatoria de las muestras de características.

Publicación traducida automáticamente

Artículo escrito por AlindGupta y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta