Prerrequisitos: Mezcla Gaussiana
Un modelo de mezcla gaussiana asume que los datos se segregan en grupos de tal manera que cada punto de datos en un grupo dado sigue una distribución gaussiana multivariada particular y las distribuciones gaussianas multivariadas de cada grupo son independientes entre sí. Para agrupar datos en dicho modelo, se debe calcular la probabilidad posterior de que un punto de datos pertenezca a un grupo determinado dados los datos observados. Un método aproximado para este propósito es el método de Baye. Pero para conjuntos de datos grandes, el cálculo de probabilidades marginales es muy tedioso. Como solo es necesario encontrar el grupo más probable para un punto dado, se pueden utilizar métodos de aproximación, ya que reducen el trabajo mecánico. Uno de los mejores métodos aproximados es utilizar el método de inferencia bayesiana variacional. El método utiliza los conceptos deDivergencia KL y aproximación de campo medio .
Los pasos a continuación demostrarán cómo implementar la inferencia bayesiana variacional en un modelo de mezcla gaussiana utilizando Sklearn. Los datos utilizados son los datos de la tarjeta de crédito que se pueden descargar desde Kaggle .
Paso 1: Importación de las bibliotecas requeridas
import numpy as np import pandas as pd import matplotlib.pyplot as plt from sklearn.mixture import BayesianGaussianMixture from sklearn.preprocessing import normalize, StandardScaler from sklearn.decomposition import PCA
Paso 2: Cargar y Limpiar los datos
# Changing the working location to the location of the data
cd "C:\Users\Dev\Desktop\Kaggle\Credit_Card"
# Loading the Data
X = pd.read_csv('CC_GENERAL.csv')
# Dropping the CUST_ID column from the data
X = X.drop('CUST_ID', axis = 1)
# Handling the missing values
X.fillna(method ='ffill', inplace = True)
X.head()

Paso 3: preprocesamiento de los datos
# Scaling the data to bring all the attributes to a comparable level scaler = StandardScaler() X_scaled = scaler.fit_transform(X) # Normalizing the data so that the data # approximately follows a Gaussian distribution X_normalized = normalize(X_scaled) # Converting the numpy array into a pandas DataFrame X_normalized = pd.DataFrame(X_normalized) # Renaming the columns X_normalized.columns = X.columns X_normalized.head()

Paso 4: Reducir la dimensionalidad de los datos para hacerlos visualizables
# Reducing the dimensions of the data pca = PCA(n_components = 2) X_principal = pca.fit_transform(X_normalized) # Converting the reduced data into a pandas dataframe X_principal = pd.DataFrame(X_principal) # Renaming the columns X_principal.columns = ['P1', 'P2'] X_principal.head()
Los dos parámetros principales de la clase de mezcla bayesiana gaussiana son n_components y covariance_type .
- n_components: Determina el número máximo de clusters en los datos dados.
- covariance_type: Describe el tipo de parámetros de covarianza a utilizar.
Puede leer sobre todos los demás atributos en su documentación .
En los pasos que se indican a continuación, el parámetro n_components se fijará en 5, mientras que el parámetro covariance_type variará en todos los valores posibles para visualizar el impacto de este parámetro en el agrupamiento.
Paso 5: construir modelos de agrupamiento para diferentes valores de covariance_type y visualizar los resultados
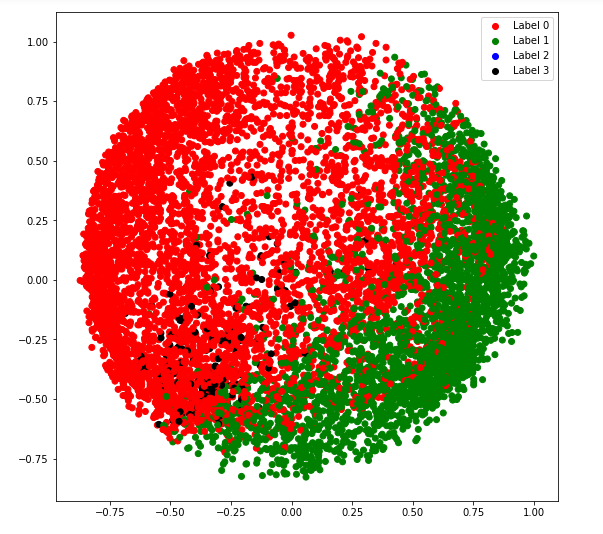
a) tipo_covarianza = ‘completo’
# Building and training the model vbgm_model_full = BayesianGaussianMixture(n_components = 5, covariance_type ='full') vbgm_model_full.fit(X_normalized) # Storing the labels labels_full = vbgm_model_full.predict(X) print(set(labels_full))
colours = {}
colours[0] = 'r'
colours[1] = 'g'
colours[2] = 'b'
colours[3] = 'k'
# Building the colour vector for each data point
cvec = [colours[label] for label in labels_full]
# Defining the scatter plot for each colour
r = plt.scatter(X_principal['P1'], X_principal['P2'], color ='r');
g = plt.scatter(X_principal['P1'], X_principal['P2'], color ='g');
b = plt.scatter(X_principal['P1'], X_principal['P2'], color ='b');
k = plt.scatter(X_principal['P1'], X_principal['P2'], color ='k');
# Plotting the clustered data
plt.figure(figsize =(9, 9))
plt.scatter(X_principal['P1'], X_principal['P2'], c = cvec)
plt.legend((r, g, b, k), ('Label 0', 'Label 1', 'Label 2', 'Label 3'))
plt.show()
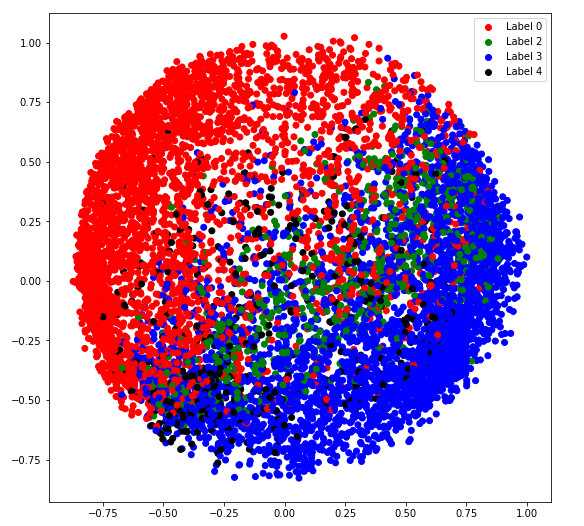
b) tipo_covarianza = ‘empatado’
# Building and training the model vbgm_model_tied = BayesianGaussianMixture(n_components = 5, covariance_type ='tied') vbgm_model_tied.fit(X_normalized) # Storing the labels labels_tied = vbgm_model_tied.predict(X) print(set(labels_tied))
colours = {}
colours[0] = 'r'
colours[2] = 'g'
colours[3] = 'b'
colours[4] = 'k'
# Building the colour vector for each data point
cvec = [colours[label] for label in labels_tied]
# Defining the scatter plot for each colour
r = plt.scatter(X_principal['P1'], X_principal['P2'], color ='r');
g = plt.scatter(X_principal['P1'], X_principal['P2'], color ='g');
b = plt.scatter(X_principal['P1'], X_principal['P2'], color ='b');
k = plt.scatter(X_principal['P1'], X_principal['P2'], color ='k');
# Plotting the clustered data
plt.figure(figsize =(9, 9))
plt.scatter(X_principal['P1'], X_principal['P2'], c = cvec)
plt.legend((r, g, b, k), ('Label 0', 'Label 2', 'Label 3', 'Label 4'))
plt.show()
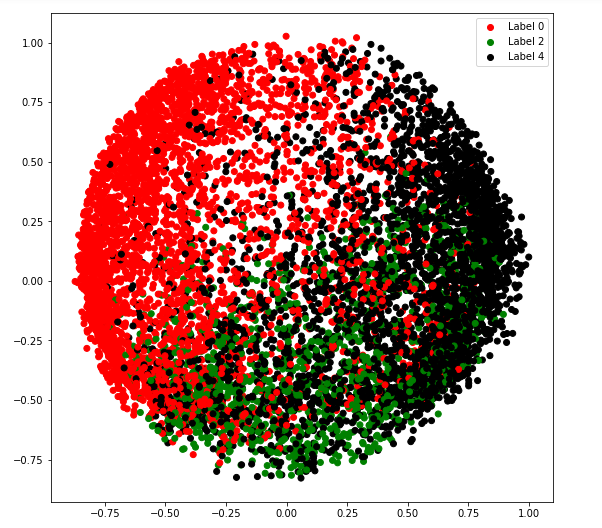
c) tipo_covarianza = ‘diag’
# Building and training the model vbgm_model_diag = BayesianGaussianMixture(n_components = 5, covariance_type ='diag') vbgm_model_diag.fit(X_normalized) # Storing the labels labels_diag = vbgm_model_diag.predict(X) print(set(labels_diag))
colours = {}
colours[0] = 'r'
colours[2] = 'g'
colours[4] = 'k'
# Building the colour vector for each data point
cvec = [colours[label] for label in labels_diag]
# Defining the scatter plot for each colour
r = plt.scatter(X_principal['P1'], X_principal['P2'], color ='r');
g = plt.scatter(X_principal['P1'], X_principal['P2'], color ='g');
k = plt.scatter(X_principal['P1'], X_principal['P2'], color ='k');
# Plotting the clustered data
plt.figure(figsize =(9, 9))
plt.scatter(X_principal['P1'], X_principal['P2'], c = cvec)
plt.legend((r, g, k), ('Label 0', 'Label 2', 'Label 4'))
plt.show()
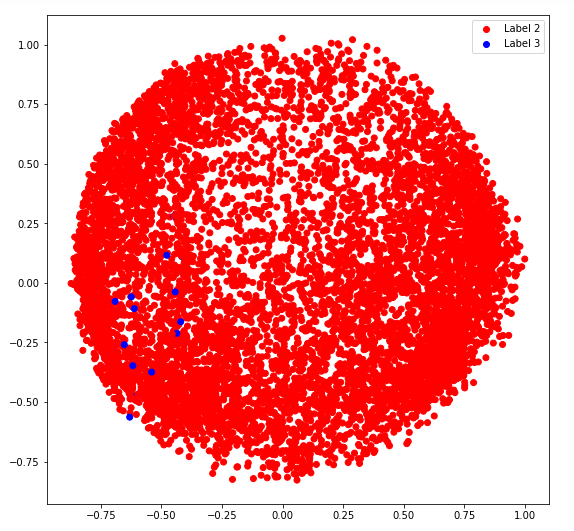
d) tipo_covarianza = ‘esférico’
# Building and training the model vbgm_model_spherical = BayesianGaussianMixture(n_components = 5, covariance_type ='spherical') vbgm_model_spherical.fit(X_normalized) # Storing the labels labels_spherical = vbgm_model_spherical.predict(X) print(set(labels_spherical))
colours = {}
colours[2] = 'r'
colours[3] = 'b'
# Building the colour vector for each data point
cvec = [colours[label] for label in labels_spherical]
# Defining the scatter plot for each colour
r = plt.scatter(X_principal['P1'], X_principal['P2'], color ='r');
b = plt.scatter(X_principal['P1'], X_principal['P2'], color ='b');
# Plotting the clustered data
plt.figure(figsize =(9, 9))
plt.scatter(X_principal['P1'], X_principal['P2'], c = cvec)
plt.legend((r, b), ('Label 2', 'Label 3'))
plt.show()
Publicación traducida automáticamente
Artículo escrito por AlindGupta y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA