ML | Introducción al optimizador de degradado basado en impulso

Gradient Descent es una técnica de optimización utilizada en marcos de Machine Learning para entrenar diferentes modelos. El proceso de entrenamiento consta de una función objetivo (o la función de error), que determina el error que tiene un modelo de Machine Learning en un conjunto de datos determinado.
Durante el entrenamiento, los parámetros de este algoritmo se inicializan a valores aleatorios. A medida que el algoritmo itera, los parámetros se actualizan de manera que nos acercamos cada vez más al valor óptimo de la función.
Sin embargo, los algoritmos de optimización adaptativa están ganando popularidad debido a su capacidad para converger rápidamente. Todos estos algoritmos, a diferencia del Descenso de Gradiente convencional, usan estadísticas de las iteraciones anteriores para fortalecer el proceso de convergencia.

Optimización basada en impulso:

Un algoritmo de optimización adaptable utiliza promedios exponencialmente ponderados de gradientes sobre iteraciones anteriores para estabilizar la convergencia, lo que da como resultado una optimización más rápida. Por ejemplo, en la mayoría de las aplicaciones del mundo real de Deep Neural Networks, el entrenamiento se lleva a cabo con datos ruidosos. Por lo tanto, es necesario reducir el efecto del ruido cuando los datos se alimentan por lotes durante la Optimización. Este problema se puede abordar utilizando promedios ponderados exponencialmente (o promedios móviles ponderados exponencialmente).

Implementación de promedios ponderados exponencialmente:

Para aproximar las tendencias en un conjunto de datos ruidoso de tamaño N:
$\theta_{0}, \theta_{1}, \theta_{2}, ..., \theta_{N}$ , mantenemos un conjunto de parámetros $v_{0}, v_{1}, v_{2}, v_{3}, ..., v_{N}$ . A medida que iteramos a través de todos los valores en el conjunto de datos, calculamos los parámetros de la siguiente manera:

On iteration t:
    Get next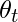

Este algoritmo promedia el valor de $v_{\theta}$ sobre sus valores de $\frac{1}{1 - \beta}$ iteraciones anteriores. Este promedio garantiza que solo se mantenga la tendencia y se promedie el ruido. Este método se utiliza como una estrategia en el descenso de gradientes basado en impulso para que sea robusto frente al ruido en las muestras de datos, lo que da como resultado un entrenamiento más rápido.
Como ejemplo, si tuviera que optimizar una función $f(x)$ en el parámetro $X$ , el siguiente pseudocódigo ilustra el algoritmo:

On iteration t:
    On the current batch, compute

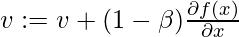
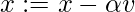
Los hiperparámetros para este algoritmo de optimización son $\alfa$ , llamados tasa de aprendizaje y $\beta$ , similar a la aceleración en mecánica.
A continuación, se muestra una implementación de Gradient Descent basado en Momentum en una función $f(x) = x ^ 2 - 4 x + 4$ :

Python3

import math
 
# HyperParameters of the optimization algorithm
alpha = 0.01
beta = 0.9
 
# Objective function
def obj_func(x):
    return x * x - 4 * x + 4
     
# Gradient of the objective function
def grad(x):
    return 2 * x - 4
     
# Parameter of the objective function
x = 0
 
# Number of iterations
iterations = 0
 
v = 0
 
while (1):
    iterations += 1
    v = beta * v + (1 - beta) * grad(x)
     
    x_prev = x
     
    x = x - alpha * v
     
    print("Value of objective function on iteration", iterations, "is", x)
     
    if x_prev == x:
        print("Done optimizing the objective function. ")
        break

Publicación traducida automáticamente

Artículo escrito por Nikhil Balwani y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Optimización basada en impulso:

Implementación de promedios ponderados exponencialmente:

Python3

Deja una respuesta Cancelar la respuesta