0/1 Mochila usando Rama y Atado

Branch andbound es un paradigma de diseño de algoritmos que generalmente se usa para resolver problemas de optimización combinatoria. Estos problemas suelen ser exponenciales en términos de complejidad de tiempo y pueden requerir explorar todas las permutaciones posibles en el peor de los casos. Branch and Bound resuelve estos problemas con relativa rapidez. 

Consideremos a continuación el problema de la mochila 0/1 para entender Branch and Bound. Dadas dos arrays de enteros val[0..n-1] y wt[0..n-1] que representan valores y pesos asociados con n elementos respectivamente. 

Averigüe el subconjunto de valor máximo de val[] tal que la suma de los pesos de este subconjunto sea menor o igual que la capacidad de la mochila W. Exploremos todos los enfoques para este problema.

1. Un enfoque codicioso consiste en recoger los artículos en orden decreciente de valor por unidad de peso. El enfoque Greedy solo funciona para el problema de la mochila fraccional y es posible que no produzca un resultado correcto para la mochila 0/1 .
2. Podemos utilizar la programación dinámica ( DP ) para el problema de la mochila 0/1 . En DP, usamos una tabla 2D de tamaño nx W. La solución DP no funciona si los pesos de los artículos no son números enteros .
3. Dado que la solución DP no siempre funciona, una solución es usar Brute Force . Con n elementos, hay 2 ⁿ soluciones para generar, verifique cada una para ver si satisfacen la restricción, guarde la solución máxima que satisface la restricción. Esta solución se puede expresar como árbol . 
   • 
4. Podemos usar Backtracking para optimizar la solución Brute Force. En la representación de árbol, podemos hacer DFS de árbol. Si llegamos a un punto en el que la solución ya no es factible, no hay necesidad de seguir explorando. En el ejemplo dado, el retroceso sería mucho más efectivo si tuviéramos aún más artículos o una capacidad de mochila más pequeña.
   • 

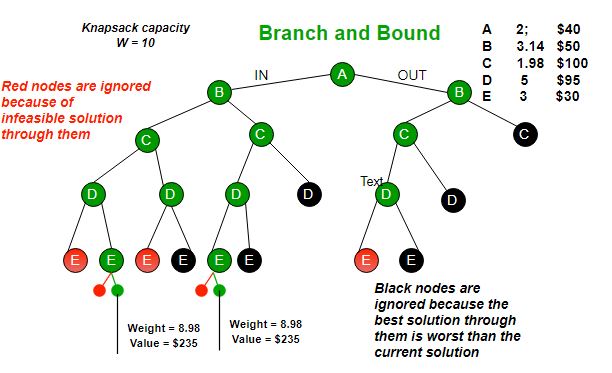
 Branch and Bound La solución basada en backtracking funciona mejor que la fuerza bruta al ignorar soluciones inviables. Podemos hacerlo mejor (que retroceder) si conocemos un límite en el subárbol de la mejor solución posible enraizado con cada Node. Si lo mejor en el subárbol es peor que lo mejor actual, simplemente podemos ignorar este Node y sus subárboles. Entonces calculamos el límite (la mejor solución) para cada Node y comparamos el límite con la mejor solución actual antes de explorar el Node. Los límites de ejemplo utilizados en el siguiente diagrama son: A abajo puede dar $315, B abajo puede $275, C abajo puede $225, D abajo puede $125 y E abajo puede $30. En el próximo artículo , hemos discutido el proceso para obtener estos límites. 

 

Ramificar y acotar es una técnica muy útil para buscar una solución, pero en el peor de los casos, necesitamos calcular completamente todo el árbol. En el mejor de los casos, solo necesitamos calcular completamente un camino a través del árbol y podar el resto. 

Fuente: 

Las imágenes y el contenido de arriba se adoptaron del siguiente enlace agradable. http://www.cse.msu.edu/~torng/Classes/Archives/cse830.03fall/Lectures/Lecture11.ppt   Ramificar y enlazar | Set 2 (Implementación de 0/1 Mochila) 

Este artículo es una contribución de Utkarsh Trivedi. Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo y enviarlo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks. Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.