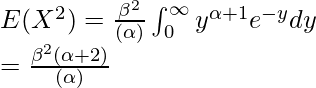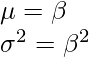Modelo de Distribución Gamma en Matemáticas

Introducción :

Supongamos que un evento puede ocurrir varias veces dentro de una determinada unidad de tiempo. Cuando se desconoce el número total de ocurrencias del evento, podemos considerarlo como una variable aleatoria. Ahora, si esta variable aleatoria X tiene distribución gamma, entonces su función de densidad de probabilidad se da de la siguiente manera.

only when x > 0, α >0, β >0. Otherwise f(x) = 0

donde, Γ(α) es el valor de la función gamma, definida por:

Integrando por partes, obtenemos que:

for α > 1

Así, Γ(α) = (α-1)! Cuando α es un número entero positivo.

Representado como –

X ~ GAM(β, α)

Valor esperado :

El valor esperado de la distribución de Poisson se puede encontrar sumando productos de valores con sus respectivas probabilidades.

Después de poner y = x/β, obtenemos –

Ahora, después de usar la identidad, Γ(α + 1) = α · Γ(α) , obtenemos –

μ = α β

Varianza y desviación estándar:

La varianza de la distribución gamma se puede encontrar utilizando la fórmula de varianza.

Después de poner y = x/β, obtenemos –

Pero, Γ(α + 2) = (α+1) · Γ(α+1) y Γ(α+1) = α · Γ(α)

=> Γ(α + 2) = α.(α+1).Γ(α), obtenemos –

La desviación estándar viene dada por:

Nota –

In special case if α  = 1, we get exponential distribution with