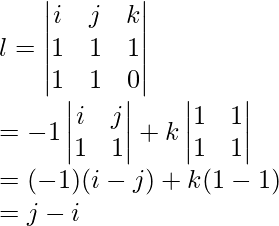Cuando un cuerpo rígido gira alrededor de un eje fijo, se denomina movimiento de rotación. El movimiento de rotación se puede ver en casi todas partes en la vida diaria. Desde las ruedas de un coche hasta las manecillas del reloj. Todos estos objetos están haciendo un movimiento de rotación alrededor de un eje fijo. Similar al movimiento lineal, el movimiento de rotación también implica velocidad, aceleración e impulso. Estas cantidades se denominan velocidad angular, aceleración angular y momento angular en el caso del movimiento de rotación. Veamos el concepto de momento angular en detalle.
Velocidad angular
Supongamos que un cuerpo gira alrededor de un eje fijo. Entonces el cuerpo cambia su ángulo con el tiempo. Denotando el ángulo por![]()
![]()
En los casos en que el movimiento de rotación no es constante, se calcula la velocidad angular instantánea.
![]()
Como se muestra en la figura, la velocidad angular está dirigida hacia el eje fijo. La velocidad lineal “v” de la partícula también se puede expresar en términos de la velocidad angular.
![]()
Momento angular
El movimiento de un cuerpo rígido se compone de movimiento de traslación y movimiento de rotación. Se sabe que se necesita fuerza para poner el cuerpo en movimiento de traslación. El par es análogo a la fuerza en el movimiento de rotación. Torque trae un cambio en el momento angular del sistema. El momento angular es análogo al momento lineal en el caso del movimiento de traslación.
En la figura se da una partícula cuyo vector de posición con respecto al origen O es “r”. «p» denota el momento lineal de la partícula que se mueve alrededor de ese punto. En ese caso, el momento angular está dado por,
l = r × pag
Este es el producto cruzado del vector de posición y el vector de momento lineal.
La magnitud del vector está dada por,
l = rpsen()
La relación entre el par y la fuerza también se puede derivar de estas ecuaciones. Derivando la ecuación anterior,
l = r × pag
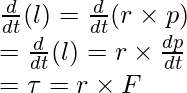
Momento angular de un sistema de partículas
A menudo, los cuerpos no son masas puntuales. Contienen más de una partícula. Supongamos que el cuerpo consta de n partículas, cada una de las cuales tiene un vector de posición r i y un momento denotado por p i . En ese caso, el momento angular del sistema viene dado por la suma vectorial del momento individual de las partículas.
L = l 1 + l 2 + l 3 + .. l norte
Cada partícula tiene un momento angular que viene dado por,
l yo = r yo xp yo
L = r 1 xp 1 + r 2 xp 2 + r 3 xp 3 …. r n xp n
Problemas de muestra
Pregunta 1: Encuentra el momento angular de la partícula que gira alrededor del origen a una distancia de 5 m con un momento lineal de 50 kg/s.
Responder:
El momento angular está dado por,
l = rpsen()
Dado: r = 5 m, p = 50 Kgm/s y θ = 90°.
l = rpsin(θ)
l = (5)(50)sen(90)
l = 250
Pregunta 2: Encuentra el momento angular de una partícula que gira alrededor del origen a una distancia de 10 m con un momento lineal de 10 kg/s. El ángulo entre el vector de posición y el momento es de 30°.
Responder:
El momento angular está dado por,
l = rpsen()
Dado: r = 10m, p = 10Kgm/
l = rpsin(θ)
l = (10)(10)sen(30)
l = 50
Pregunta 3: Encuentra el momento angular de una partícula que gira alrededor del origen a una distancia de 1,5 m con un momento lineal de 100 kgm/s. El ángulo entre el vector de posición y el momento es de 60°.
Responder:
El momento angular está dado por,
l = rpsin(θ)
Dado: r = 5 m, p = 50 kgm/s
l = rpsin(θ)
l = (1.5)(100)sen(60)
l = 75√3
Pregunta 4: El vector de posición y el momento lineal de un cuerpo vienen dados por r = 3i + 4j + km y p = 5j Kg/s. Encuentre el momento angular.
Responder:
El momento angular está dado por,
l = r × pag
Dado: r = 3i + 4j + k, p = 5j.
Pregunta 5: El vector de posición y el momento lineal de un cuerpo están dados por r = i + j + km y p = i + j Kg/s. Encuentre el momento angular.
Responder:
El momento angular está dado por,
l = r × pag
Dado: r = i + j + k, p = i + j
Pregunta 6: Encuentra el momento angular del sistema de dos partículas que giran alrededor del origen a una distancia de 5 m con un momento lineal de 50 Kg/s y 10 Kg/s.
Responder:
El momento angular está dado por,
l = rpsin(θ)
Dado: r = 5 m, p 1 = 50 Kgm/s, p 2 = 10 Kgm/s y el ángulo es un ángulo recto.
Dado que el sistema consta de dos partículas. El momento angular total será la suma del momento angular de estas partículas.
l = rp 1 + rp 2
l = (5)(50) + (5)(10)
l = 250 + 50
l = 300
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA