Es un árbol binario que tiene las siguientes propiedades:
(1) Cada clave en el subárbol derecho de un Node es mayor que la clave almacenada en el Node mismo, (
2) La raíz no tiene un hijo izquierdo y
(3) Las hojas solo se encuentran en los dos últimos niveles del árbol.
Se utiliza para implementar colas de prioridad. La razón por la que un usuario puede preferir un almacenamiento dinámico débil sobre un almacenamiento dinámico binario es que los almacenamientos dinámicos débiles son capaces de realizar menos comparaciones de elementos en el peor de los casos.
Las complejidades de tiempo en el peor de los casos de inserción y eliminación de una implementación basada en arreglos de un montón débil son: 1.
insertar: O (lg n)
2. eliminar: O (lg n)
La construcción de almacenamiento dinámico débil utiliza un búfer que admite la inserción en tiempo constante. Se inserta un nuevo elemento en el búfer siempre que el tamaño del búfer esté por debajo de un umbral. Una vez que el búfer está lleno, todos los elementos del búfer se mueven al montón débil.
Se obtiene un montón débil al aflojar los requisitos de un montón binario. Para representar un montón débil en la memoria, se utilizan dos arrays. El primero es el arreglo de elementos a y el otro es un arreglo r de bits inversos.
Usamos ![]() para referirnos al elemento en el índice i de la array a o a un Node en la estructura de árbol correspondiente. Se construye un montón débil de tal manera que, para
para referirnos al elemento en el índice i de la array a o a un Node en la estructura de árbol correspondiente. Se construye un montón débil de tal manera que, para ![]() , el índice de su hijo izquierdo es
, el índice de su hijo izquierdo es ![]() , el índice de su hijo derecho es
, el índice de su hijo derecho es ![]() y (donde i != 0) el índice de su padre es
y (donde i != 0) el índice de su padre es ![]() .
.
Montón débil Ejemplo:
si se dan 10 enteros como entrada, por ejemplo, 8, 7, 4, 5, 2, 6, 9, 3, 11, 1, entonces el montón débil construido a partir de la siguiente entrada será como se muestra en el diagrama abajo.
Operaciones en el montón débil y cómo se logran las complejidades de tiempo deseadas usando estas operaciones
Las operaciones básicas del montón débil junto con el pseudocódigo son las siguientes:
1. Antepasado distinguido: El antepasado distinguido de ![]() , j != 0, es el padre de
, j != 0, es el padre de ![]() si
si ![]() es hijo derecho, y el antepasado distinguido del padre de
es hijo derecho, y el antepasado distinguido del padre de ![]() si
si ![]() es hijo izquierdo. Usamos d-antepasado (j) para denotar el índice de dicho antepasado. La ordenación del montón débil impone que ningún elemento sea más pequeño que el de su ancestro distinguido.
es hijo izquierdo. Usamos d-antepasado (j) para denotar el índice de dicho antepasado. La ordenación del montón débil impone que ningún elemento sea más pequeño que el de su ancestro distinguido.
// Finding the distinguished ancestor in a weak heap
procedure: d-ancestor
input: j: index
while (j & 1) = 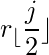
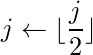 return
return 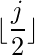
2. Unirse: la subrutina combina dos montones débiles en un montón débil condicionado a las siguientes configuraciones. Unirse requiere un tiempo de O(1) e implica una comparación de elementos.
// Joining two weak heaps
procedure: join
input: i, j: indices
if ( ){
swap(
){
swap(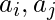 )
)
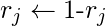 return false
}
return true
return false
}
return true
3. Construir: se puede construir un montón débil de tamaño n mediante ![]() comparaciones de elementos realizando
comparaciones de elementos realizando ![]() llamadas a la subrutina de unión.
llamadas a la subrutina de unión.
//Constructing a weak heap
procedure: construct
input: a: array of n elements; r: array of n bits
for i 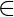 {0, 1, . . ., n
{0, 1, . . ., n  1}
1}
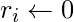 for j
for j 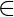 {n
{n  1, n
1, n  2, . . ., 1}
2, . . ., 1}
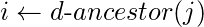 join(i, j)
join(i, j)
4. Sift-up: La subrutina sift-up(j) se utiliza para restablecer la ordenación de pila débil entre el elemento e, inicialmente en la ubicación j, y los antecesores de ![]() . Comenzando desde la ubicación j, mientras que e no está en la raíz y es más pequeño que el elemento en su ancestro distinguido, intercambiamos los dos elementos, cambiamos el bit del Node que anteriormente contenía e y repetimos desde la nueva ubicación de e.
. Comenzando desde la ubicación j, mientras que e no está en la raíz y es más pequeño que el elemento en su ancestro distinguido, intercambiamos los dos elementos, cambiamos el bit del Node que anteriormente contenía e y repetimos desde la nueva ubicación de e.
// reestablishing the weak-heap ordering
// on the path from 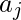 upwards
procedure: sift-up
input: j: index
while (j != 0){
upwards
procedure: sift-up
input: j: index
while (j != 0){
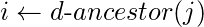 if join(i, j){
break
}
if join(i, j){
break
}
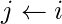 }
}
5. Insertar: para insertar un elemento e, primero agregamos e a la siguiente entrada de array disponible, convirtiéndola en una hoja en el montón. Si esta hoja es el único hijo de su padre, la convertimos en un hijo izquierdo actualizando el bit inverso en el padre. Para restablecer el orden del montón débil, llamamos a la subrutina tamizar desde la ubicación de e. De ello se deduce que la inserción requiere un tiempo O(lg n) e implica, como máximo, ![]() comparaciones de elementos.
comparaciones de elementos.
// Inserting an element into a weak heap.
procedure: insert
input: a: array of n elements; r: array of n bits; e: element
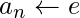
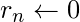 if( (n & 1) = 0){
if( (n & 1) = 0){
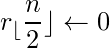 }
sift-up(n)
++n
}
sift-up(n)
++n
6. Sift-down: La subrutina sift-down(j) se utiliza para restablecer la ordenación de pila débil entre el elemento en la ubicación j y los del subárbol derecho de ![]() . A partir del hijo derecho de , se identifica
. A partir del hijo derecho de , se identifica ![]() el último Node en la columna izquierda del subárbol derecho de ;
el último Node en la columna izquierda del subárbol derecho de ; ![]() esto se hace visitando repetidamente hijos izquierdos hasta llegar a un Node que no tiene hijo izquierdo. El camino desde este Node hasta el hijo derecho de
esto se hace visitando repetidamente hijos izquierdos hasta llegar a un Node que no tiene hijo izquierdo. El camino desde este Node hasta el hijo derecho de ![]() se recorre hacia arriba, y las operaciones de unión se realizan repetidamente entre
se recorre hacia arriba, y las operaciones de unión se realizan repetidamente entre ![]() y los Nodes a lo largo de este camino. Después de cada combinación, el elemento en la ubicación j es menor o igual que todos los elementos del subárbol izquierdo del Node considerado en la siguiente combinación.
y los Nodes a lo largo de este camino. Después de cada combinación, el elemento en la ubicación j es menor o igual que todos los elementos del subárbol izquierdo del Node considerado en la siguiente combinación.
7. delete-min: para realizar delete-min, el elemento almacenado en la raíz del montón débil se reemplaza con el almacenado en la última entrada de array ocupada. Para restaurar el orden de almacenamiento dinámico débil, se llama a una criba para la nueva raíz. Por lo tanto, delete-min requiere un tiempo O(lg n) e implica como máximo comparaciones de elementos lg n.
Relación del montón débil con el montón binario y el montón binomial
La estructura del montón débil es la misma que la disposición del árbol binario. Un montón débil perfecto que almacena ![]() elementos exactos es una representación de árbol binario de un árbol binomial ordenado por montón de rango r. El Node k tiene un hijo izquierdo con un índice de 2k y un hijo derecho con un índice de 2k + 1, suponiendo que la raíz está en el índice 0 (en el montón binario era 2k+1 para el hijo izquierdo y 2k+2 para el hijo derecho) . La única diferencia es que la raíz del montón débil no tiene un hijo izquierdo, solo un hijo derecho, que se almacena en un índice de 2*0+1=1.
elementos exactos es una representación de árbol binario de un árbol binomial ordenado por montón de rango r. El Node k tiene un hijo izquierdo con un índice de 2k y un hijo derecho con un índice de 2k + 1, suponiendo que la raíz está en el índice 0 (en el montón binario era 2k+1 para el hijo izquierdo y 2k+2 para el hijo derecho) . La única diferencia es que la raíz del montón débil no tiene un hijo izquierdo, solo un hijo derecho, que se almacena en un índice de 2*0+1=1.
Además, la estructura de Weak Heap es muy similar a un montón binomial, con un árbol de altura h compuesto por una raíz más árboles de alturas h – 1, h – 2, …, 1. Al igual que los montones binomiales, la operación fundamental en los débiles montones está fusionando dos montones de igual altura h, para hacer un montón débil de altura h+1. Esto requiere exactamente una comparación, entre las raíces. Cualquiera que sea la raíz mayor (suponiendo un montón máximo) es la raíz final. El primer hijo de la raíz final es la raíz perdedora, que retiene a sus hijos (subárbol derecho). Los hijos de la raíz ganadora se insertan como hermanos de la raíz perdedora.
Las propiedades distinguibles de un montón débil son:
1) Puede ser imperfecto (en contraste con un árbol binomial);
2) Es un solo árbol (en contraste con una cola binomial, que es una colección de árboles perfectos);
3) Está bastante equilibrado.
Aplicaciones de almacenamiento dinámico débil
1. Se puede utilizar como un paso intermedio para la construcción eficiente de almacenamiento dinámico binario.
2. Una variante de almacenamiento dinámico débil, que permite que algunos de los narices violen el orden del almacenamiento dinámico débil, se utiliza para la búsqueda de gráficos y la optimización de redes, y se sabe que es probablemente mejor que un almacenamiento dinámico de Fibonacci.