Moore – Penrose Pseudoinverse en R Programación

El concepto utilizado para generalizar la solución de una ecuación lineal se conoce como Moore – Penrose Pseudoinverse of a matrix. La inversa de Moore-Penrose es el tipo más conocido de array pseudoinversa. En álgebra lineal, la pseudoinversa $A^{+}$ de una array A es una generalización de la array inversa. El uso más común de la pseudoinversa es calcular la solución que mejor se ajusta a un sistema de ecuaciones lineales que carece de una solución única. El término inversa generalizada se usa a veces como sinónimo de pseudoinverso. R Language proporciona un método muy simple para calcular Moore – Penrose Pseudoinverse. La pseudoinversa se usa de la siguiente manera:

$x = A^{+} b$

donde,
A ⁺ : descomposición de valor único utilizada para calcular la pseudoinversa o la inversa generalizada de una array numérica
x y b: vectores

Nota: La pseudoinversa de Moore – Penrose resuelve el problema en el sentido del error por mínimos cuadrados. En general, no existe una solución exacta para los problemas sobredeterminados. Entonces, si verifica la solución, no obtendrá el b exacto requerido, sino un valor aproximado de b.

Implementación en R

R proporciona dos funciones ginv() que está disponible en la biblioteca MASS y pinv() que está disponible en la biblioteca pracma para calcular la inversa generalizada de Moore-Penrose de una array. Estas dos funciones devuelven una inversa generalizada arbitraria de una array, utilizando gaussianElimination.

Sintaxis:
ginv(A)
pinv(A)
Parámetro:
A: array numérica

Ejemplo 1:
Considere a continuación 3 ecuaciones lineales:

$x_1 + 3x_2 = 17\\ 5x_1 + 7x_2 = 19\\ 11x_1 + 13x_2 = 23$

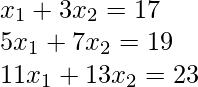
De manera equivalente, se pueden escribir las ecuaciones anteriores en forma de array como se muestra a continuación:

$A{x} = {b}\\$

$\begin{bmatrix} 1 & 3 \\ 5 & 7 \\ 11 & 13 \\ \end{bmatrix} % \begin{bmatrix} x_1\\ x_2\\ \end{bmatrix} = \begin{bmatrix} 17\\ 19\\ 23\\ \end{bmatrix}$

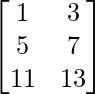
# Usando ginv()

Python3

# R program to illustrate
# solve a linear matrix
# equation of metrics using
# moore – Penrose Pseudoinverse
 
# Importing library for
# applying pseudoinverse
library(MASS)
 
# Representing A in
# matrics form in R
A = matrix(
  c(1, 5, 11, 3, 7, 13),
  nrow = 3,            
  ncol = 2,            
)
cat("A = :\n")
print(A)
 
# Representing b in
# matrics form in R
b = matrix(
  c(17, 19, 23),
  nrow = 3,            
  ncol = 1,            
)
cat("b = :\n")
print(b)
 
# Calculating x using ginv()
cat("Solution of linear equations
    using pseudoinverse:\n")
x = ginv(A) %*% b
print(x)

Producción:

A = :
     [, 1] [, 2]
[1, ]    1    3
[2, ]    5    7
[3, ]   11   13
b = :
     [, 1]
[1, ]   17
[2, ]   19
[3, ]   23
Solution of linear equations 
    using pseudoinverse:
          [, 1]
[1, ] -7.513158
[2, ]  8.118421

# Usando pinv()

Python3

# R program to illustrate
# solve a linear matrix
# equation of metrics using
# moore – Penrose Pseudoinverse
 
# Importing library for
# applying pseudoinverse
library(pracma)
 
# Representing A in
# matrics form in R
A = matrix(
  c(1, 5, 11, 3, 7, 13),
  nrow = 3,         
  ncol = 2,         
)
cat("A = :\n")
print(A)
 
# Representing b in
# matrics form in R
b = matrix(
  c(17, 19, 23),
  nrow = 3,         
  ncol = 1,         
)
cat("b = :\n")
print(b)
 
# Calculating x using pinv()
cat("Solution of linear equations
    using pseudoinverse:\n")
x = pinv(A) %*% b
print(x)

Producción:

A = :
     [, 1] [, 2]
[1, ]    1    3
[2, ]    5    7
[3, ]   11   13
b = :
     [, 1]
[1, ]   17
[2, ]   19
[3, ]   23
Solution of linear equations 
    using pseudoinverse:
          [, 1]
[1, ] -7.513158
[2, ]  8.118421

Ejemplo 2:
Del mismo modo, tengamos ecuaciones lineales en forma de array como se muestra a continuación:

$\begin{bmatrix} 1 & 2 & 3 \\ 0 & 0 & 1 \\ \end{bmatrix} % \begin{bmatrix} x_1\\ x_2\\ x_3\\ \end{bmatrix} = \begin{bmatrix} 2\\ 1\\ \end{bmatrix}$

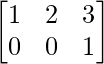
# Usando ginv()

Python3

# R program to illustrate
# solve a linear matrix
# equation of metrics using
# moore – Penrose Pseudoinverse
 
# Importing library for
# applying pseudoinverse
library(MASS)
 
# Representing A in
# matrics form in R
A = matrix(
  c(1, 0, 2, 0, 3, 1),
  ncol = 3,
  byrow = F
)
cat("A = :\n")
print(A)
 
# Representing b in
# matrics form in R
b = matrix(
  c(2, 1),
)
cat("b = :\n")
print(b)
 
# Calculating x using ginv()
cat("Solution of linear equations
    using pseudoinverse:\n")
x = ginv(A) %*% b
print(x)

Producción:

A = :
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    0    0    1
b = :
     [, 1]
[1, ]    2
[2, ]    1
Solution of linear equations 
    using pseudoinverse:
     [, 1]
[1, ] -0.2
[2, ] -0.4
[3, ]  1.0

# Usando pinv()

Python3

# R program to illustrate
# solve a linear matrix
# equation of metrics using
# moore – Penrose Pseudoinverse
 
# Importing library for
# applying pseudoinverse
library(pracma)
 
# Representing A in
# matrics form in R
A = matrix(
  c(1, 0, 2, 0, 3, 1),
  ncol = 3,
  byrow = F
)
cat("A = :\n")
print(A)
 
# Representing b in
# matrics form in R
b = matrix(
  c(2, 1),
)
cat("b = :\n")
print(b)
 
# Calculating x using pinv()
cat("Solution of linear equations
    using pseudoinverse:\n")
x = pinv(A) %*% b
print(x)

Producción:

A = :
     [, 1] [, 2] [, 3]
[1, ]    1    2    3
[2, ]    0    0    1
b = :
     [, 1]
[1, ]    2
[2, ]    1
Solution of linear equations 
    using pseudoinverse:
     [, 1]
[1, ] -0.2
[2, ] -0.4
[3, ]  1.0

Publicación traducida automáticamente

Artículo escrito por AmiyaRanjanRout y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Implementación en R

Python3

Python3

Python3

Python3

Deja una respuesta Cancelar la respuesta