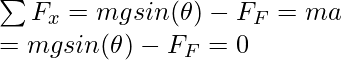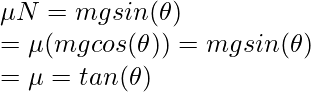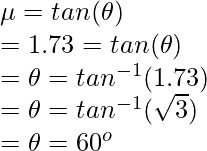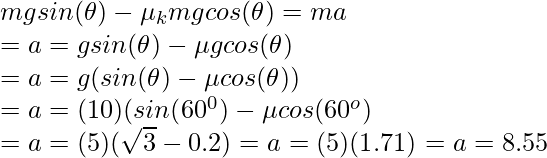La fricción es una fuerza que resiste el movimiento entre dos superficies. Si bien es principalmente responsable de la resistencia contra el movimiento, también es responsable del movimiento. Sin fricción, ningún movimiento sería posible. Cuando se trata de objetos sólidos que se mueven entre sí, existen principalmente dos tipos de fricción: fricción cinética y fricción estática. Esta fricción se opone al movimiento del cuerpo mantenido sobre una superficie. Cuando se trata de planos inclinados, hay más de dos fuerzas actuando sobre el cuerpo. Es esencial estudiar la fricción y el movimiento resultante en tales superficies.
Fricción
Las fuerzas de fricción se oponen al movimiento entre dos objetos. Cuando se trata de objetos sólidos, sentarse sobre una superficie rugosa. Hay dos tipos de fricción que actúan sobre los objetos. Estas fuerzas de fricción dependen del tipo de superficie y de las fuerzas que se aplican normalmente sobre la superficie. La siguiente figura muestra la dirección de la fuerza y la fricción sobre un bloque colocado sobre una superficie rugosa. La fuerza de fricción que actúa, en este caso, puede ser de dos tipos:
- Fricción estática
- Friccion kinetica
Fricción estática: esta fricción antes de que la caja comience a moverse. En este caso, la fricción es igual a la fuerza aplicada. A medida que aumenta la fuerza aplicada, también lo hace la fricción. Si la fuerza sigue aumentando, la fricción también aumenta, pero llega un momento en que la caja comienza a moverse. El punto justo antes de que la caja se deslice se llama movimiento de impedimento. En este punto, la fricción estática es máxima. Está determinado por el coeficiente de fricción estática.
Fórmula para la fricción estática
Fricción cinética: la fricción cinética comienza a actuar cuando la caja comienza a moverse. Su valor es menor que la fricción estática máxima. En este caso, no importa cuál sea la fuerza aplicada, el valor de la fricción cinética seguirá siendo el mismo. En este caso, está determinado por el coeficiente de fricción cinética.
Fórmula para la fricción cinética:
Movimiento en plano inclinado irregular
El movimiento de un bloque sobre un plano inclinado rugoso es la interacción de dos tipos diferentes de fuerzas. Los lugares en tal superficie experimentan tanto la fuerza gravitacional como la fuerza de fricción. Mientras que las fuerzas gravitatorias intentan tirar hacia abajo del bloque, la fuerza de fricción por su naturaleza se opone al movimiento del bloque. La siguiente figura muestra un bloque mantenido en un plano inclinado rugoso. En este punto, el bloque está en reposo porque las fuerzas de fricción pueden equilibrar las fuerzas que actúan sobre el bloque.
Veamos las fuerzas que actúan sobre el bloque. La fuerza gravitacional actúa sobre el bloque en dirección hacia abajo. Esta fuerza se puede dividir en dos componentes, uno que actúa paralelo a la superficie y otro componente que actúa perpendicular a la superficie del plano. La componente normal a la superficie del plano es responsable de la fricción. La siguiente figura muestra las diferentes fuerzas que actúan sobre el bloque.
El diagrama de cuerpo libre anterior se puede usar para encontrar los valores de los diferentes componentes de las fuerzas que actúan sobre el sistema. No hay movimiento en la dirección perpendicular a la superficie, lo que significa que las fuerzas deben equilibrarse en esta dirección.
F y = mgsen() – N = 0
De manera similar, las fuerzas a lo largo de la dirección del plano deben dar lugar a la aceleración del bloque. Suponiendo que la masa del bloque es «m» y su aceleración es «a».
![]()
Aquí, F F es la fuerza de fricción. Esto puede ser fricción estática máxima, fricción estática o fricción cinética. En este caso, puede haber algunas posibilidades basadas en el ángulo de inclinación().
Caso (i): La fricción es menor que la fricción estática máxima y el cuerpo aún no ha iniciado el movimiento. En este caso, ![]() . En este caso, la fricción es igual a la componente de la fuerza de gravedad que actúa sobre el bloque.
. En este caso, la fricción es igual a la componente de la fuerza de gravedad que actúa sobre el bloque.
F F = mgsen()
Caso (ii): La fricción es igual a la fricción estática máxima y el cuerpo aún no ha iniciado el movimiento. Aquí ![]()
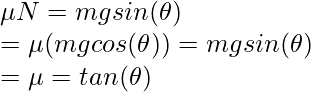
Caso (iii): La fricción es igual a la fricción cinética. En este caso, el cuerpo está en movimiento y la fuerza neta da lugar a la aceleración del cuerpo. En este caso,
![]()
Dónde 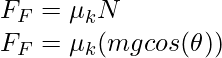
![]()
Problemas de muestra
Pregunta 1: Encuentre el valor de la fricción que actúa sobre un bloque de 5 kg mantenido en reposo sobre una superficie inclinada con un ángulo de 30°.
Responder:
Ahora, dado que el bloque está en reposo, eso significa que las fuerzas en las direcciones x e y deben estar equilibradas.
Fuerza neta en la dirección x,
La fuerza de rozamiento viene dada por,
F F = mgsen()
Dado: m = 5Kg, θ = 30°
Reemplazando los valores en la ecuación,
F F = mgsen()
⇒ F F =(5)(10)sen(30°)
⇒ F F = 25 N
Pregunta 2: Encuentre el valor de la fricción que actúa sobre un bloque de 10 kg mantenido en reposo sobre una superficie inclinada con un ángulo de 45°.
Responder:
Ahora, dado que el bloque está en reposo, eso significa que las fuerzas en las direcciones x e y deben estar equilibradas.
Fuerza neta en la dirección x,
La fuerza de rozamiento viene dada por,
F F = mgsen()
Dado: m = 10Kg, θ = 45°
Reemplazando los valores en la ecuación,
F F = mgsen(θ)
⇒ F F =(10)(10)sen(45°)
⇒ F F =50√2
⇒ F F = 50(1.414)
⇒ F F = 70.7 N
Pregunta 3: Encuentre el ángulo de la superficie inclinada en el que el bloque sostenido sobre ella comenzará a deslizarse, dado que el coeficiente de fricción estática es 1.73.
Responder:
Este es el caso (ii) mencionado anteriormente. El bloque está a punto de resbalar. En este caso,
Dado
Conectando a la ecuación anterior,
Pregunta 4: Encuentra el ángulo de la superficie inclinada en el que el bloque sostenido sobre ella comenzará a deslizarse, dado que el coeficiente de fricción estática es 1.73.
Responder:
Este es el caso (ii) mencionado anteriormente. El bloque está a punto de resbalar. En este caso,
Dado
Conectando a la ecuación anterior,
Pregunta 5: Encuentra la aceleración de un bloque (m = 50Kg) mantenido en un plano inclinado con un ángulo de 60°. Dado ![]()
Responder:
tan(60) = √3 = 1,7313
Dado que tan(θ) >
Este es el caso (iiI) mencionado anteriormente. El bloque se deslizará en este caso,
Dónde
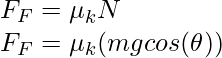
Dado:
, m = 50Kg y θ = 60°.
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA