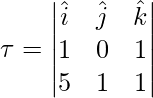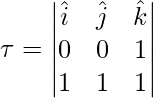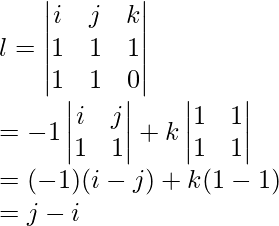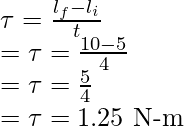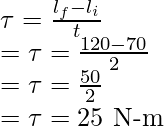Movimiento de un cuerpo rígido

Un cuerpo rígido es un cuerpo sólido que tiene poca o ninguna deformación cuando se aplica una fuerza. Cuando se aplican fuerzas a tales cuerpos, estos llegan a un movimiento de traslación y rotación. Estas fuerzas cambian la cantidad de movimiento del sistema. Los cuerpos rígidos se encuentran en casi todas partes en la vida real, todos los objetos que se encuentran en la vida real son de naturaleza rígida. Se hace imprescindible estudiar el movimiento y los efectos que sobre ellos ejercen distintas fuerzas para poder predecir sus trayectorias. Este tipo de predicciones se utilizan al hacer videojuegos, robots y naves espaciales. Veamos estos conceptos en detalle.

Dinámica de cuerpos rígidos

Los conceptos de dinámica de cuerpos rígidos se desarrollaron cuando la mecánica clásica no pudo resolver problemas de movimiento y cinemática para cuerpos que no tenían masas puntuales y eran susceptibles de rotación cuando se les aplicaban fuerzas. Un cuerpo rígido puede tener dos tipos de movimientos cuando se le aplican fuerzas:

Movimiento de traducción.
Movimiento rotacional.

Movimiento de translación

Se dice que un cuerpo está en movimiento de traslación cuando todas las partículas de ese cuerpo se mueven la misma distancia en intervalos de tiempo iguales. Este movimiento puede ser rectilíneo o curvilíneo. Algunos ejemplos de movimiento de traslación incluyen: un automóvil que se mueve en línea recta, una caja que se desliza por una cuña. Este tipo de movimiento se rige por las ecuaciones de movimiento y las leyes de Newton.

Sean F ₁ , F ₂ , F ₃ , … F _n las fuerzas vectoriales que actúan sobre el cuerpo. Estas fuerzas provocan una aceleración en la dirección en la que se encuentra su resultante. Este movimiento se rige por la Ley de Newton.

$\vec{F}_{net} = m\vec{a}$

⇒ $\vec{F}_1 + \vec{F}_2 + ... \vec{F}_n = m\vec{a}$

Donde “m” es la masa del sistema y a es la aceleración resultante del cuerpo.

Movimiento rotacional

Se dice que un cuerpo está en movimiento de rotación cuando todas las partículas que lo constituyen se mueven alrededor de un eje de rotación común en la misma dirección. Es un tipo de movimiento circular. Los ejemplos de movimientos de rotación incluyen: llantas de un automóvil que se mueven en la carretera, una pelota que rueda por una cuña, etc. Similar al movimiento de traslación, este movimiento también se puede describir extendiendo las leyes y ecuaciones utilizadas en el movimiento de traslación.

Sean $\tau_1, \tau_2, \tau_3, ... \tau_n$ los pares que están actuando sobre el cuerpo. Estos pares provocan una aceleración angular en la dirección en la que se encuentra su resultante.

$\vec{\tau}_{net} = I\vec{\alpha}$

⇒ $\vec{\tau}_1 + \vec{\tau}_2 + ... \vec{\tau}_n = I\vec{\alpha}$

Donde “I” es el momento de inercia del sistema y α es la aceleración resultante del cuerpo.

Condiciones para el Equilibrio

Se dice que un cuerpo rígido está en equilibrio mecánico si ni el momento angular ni el momento lineal del cuerpo cambian con el tiempo. Esto significa que es una condición cuando el cuerpo no tiene aceleración lineal ni aceleración angular. Consideremos un cuerpo de masa “m” y un momento de inercia “I”. Suponga que sobre el cuerpo actúan varias fuerzas que también producen un momento de torsión sobre el cuerpo en diferentes direcciones. Si el cuerpo está en equilibrio mecánico, seguirá las condiciones antes mencionadas:

$\vec{F}_1 + \vec{F}_2 + ... \vec{F}_n = 0$
$\vec{\tau}_1 + \vec{\tau}_2 + ... \vec{\tau}_n = 0$

Problemas de muestra

Pregunta 1: Encuentra el momento de torsión de la fuerza sobre un cuerpo rígido cuyo centro de masa se encuentra en el origen. La fuerza es 5i + j + k mientras que el vector de posición viene dado por i + k.

Responder:

El par está dado por,

$\tau = \vec{r} \times \vec{F}$

Dado:

r = yo + k

F = 5i + j + k

$\tau = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 1 & 0 & 1 \\ 5 & 1 & 1\end{vmatrix}$

⇒ $\tau = \hat{i}(-1) -\hat{j}(1 - 5) + \hat{k}(1 - 0)$

⇒ $\tau = -\hat{i} +4\hat{j} + \hat{k}$

Pregunta 2: Encuentra el momento de torsión de la fuerza sobre un cuerpo rígido cuyo centro de masa se encuentra en el origen. La fuerza es i + j + k mientras que el vector de posición viene dado por: k.

Responder:

El par está dado por,

$\tau = \vec{r} \times \vec{F}$

Dado:

r = k

F = yo + j + k

$\tau = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 0 & 0 & 1 \\ 1 & 1 & 1\end{vmatrix}$

⇒ $\tau = \hat{i}(-1) -\hat{j}(-1) + \hat{k}(1 - 1)$

⇒ $\tau = -\hat{i} +\hat{j}$

Pregunta 3: El vector de posición y el momento lineal de un cuerpo vienen dados por r = 3i + 4j + km y p = 5j Kg/s. Encuentre el momento angular.

Responder:

El momento angular está dado por,

l = r × pag

Dado: r = 3i + 4j + k, p = 5j

$l = \begin{vmatrix} i & j & k\\ 3 & 4 & 1\\ 0 & 1 & 0 \end{vmatrix} \\ = -1\begin{vmatrix} i & k \\ 3 & 1 \end{vmatrix} \\ = (-1)(i - 3k) \\ = 3k - i$

Pregunta 4: El vector de posición y el momento lineal de un cuerpo vienen dados por r = i + j + km y p = i + j Kg/s. Encuentre el momento angular.

Responder:

El momento angular está dado por,

l = r × pag

Dado: r = i + j + k, p = i + j

$l = \begin{vmatrix} i & j & k\\ 1 & 1 & 1\\ 1 & 1 & 0 \end{vmatrix} \\ = -1\begin{vmatrix} i & j \\ 1 & 1 \end{vmatrix} + k\begin{vmatrix} 1 & 1 \\ 1 & 1 \end{vmatrix} \\ = (-1)(i - j) + k(1 -1)\\ = j - i$

Pregunta 5: Un cuerpo gira alrededor de un eje en un movimiento circular con un radio de 0,1 m, el momento del cuerpo está dado por 50 Kgm/s. Se aplica un par de torsión sobre el cuerpo durante 4 segundos y la cantidad de movimiento se convierte en 100 kgm/s. Encuentre el torque aplicado al cuerpo.

Responder:

El momento angular de un cuerpo está dado por,

l = r × pag

Donde r es la distancia perpendicular de la fuerza desde el eje de rotación y p es el momento lineal.

La tasa de cambio en el momento angular nos da el par.

Momento angular inicial

l _yo = 0.1 × 50

yo ₌ 5

Momento angular final

l _yo = 0.1 × 100

yo ₌ 10

Tasa de cambio del momento angular = $\frac{l_f - l_i}{t}$

$\tau = \frac{l_f - l_i}{t } \\ = \tau = \frac{10 - 5}{4} \\ = \tau = \frac{5}{4} \\ = \tau = 1,25 \text{nm}$

Pregunta 6: Un cuerpo gira alrededor de un eje en un movimiento circular con un radio de 0,2 m, el momento del cuerpo está dado por 70 Kg/s. Se aplica un par de torsión sobre el cuerpo durante 2 segundos y la cantidad de movimiento se convierte en 120 kgm/s. Encuentre el torque aplicado al cuerpo.

Responder:

El momento angular de un cuerpo está dado por,

l = r × pag

Donde r es la distancia perpendicular de la fuerza desde el eje de rotación y p es el momento lineal.

La tasa de cambio en el momento angular nos da el par.

Momento angular inicial

l _yo = 0.2 × 70

yo ₌ 14

Momento angular final

l _yo = 0.2 × 120

yo ₌ 24

Tasa de cambio del momento angular = $\frac{l_f - l_i}{t}$

$\tau = \frac{l_f - l_i}{t } \\ = \tau = \frac{120 - 70}{2} \\ = \tau = \frac{50}{2} \\ = \tau = 25 \text{nm}$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Dinámica de cuerpos rígidos

Problemas de muestra

Deja una respuesta Cancelar la respuesta