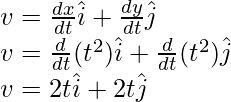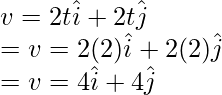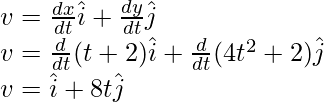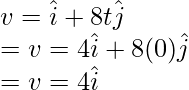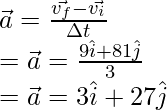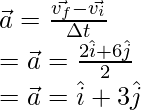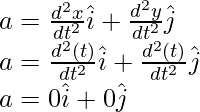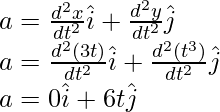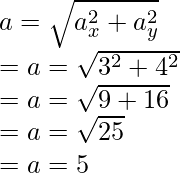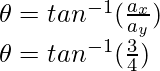Movimiento en dos dimensiones

Una partícula que se mueve en un plano se puede describir usando las coordenadas. Pero a menudo esta información no es suficiente para describir completamente el estado y el comportamiento de la partícula. Todavía quedan algunas preguntas sin respuesta. Por ejemplo, ¿qué tan rápido se está moviendo? ¿En qué dirección y cuál es la aceleración y la dirección de aceleración de la partícula? Estos parámetros son necesarios para describir el movimiento de la partícula en un plano 2D. Afortunadamente, todo esto se puede resolver usando un poco de álgebra vectorial y cálculo. Veamos cómo hacerlo en detalle.

Movimiento en un plano

Supongamos que una partícula se mueve desde un punto X en el plano cartesiano hasta un punto Y. Los vectores de posición son necesarios para describir la posición actual de la partícula. Estos vectores son siempre con respecto al marco de referencia en el origen. Se requieren los siguientes parámetros para describir completamente el comportamiento de una partícula que se mueve en un plano,

Posición
Velocidad
Aceleración

Vector de posición

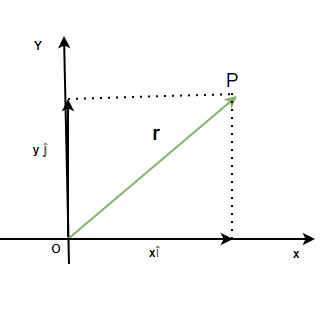
El vector que denota la posición y la dirección de la posición de la partícula con respecto al origen se llama vector de posición. El vector $\vec{r}$ de posición de una partícula está dado por,

$\vec{r} = x\hat{i} + y\hat{j}$

Donde x e y son sus componentes a lo largo del eje x e y.

Velocidad

La velocidad de una partícula se puede describir de dos maneras: velocidad promedio y velocidad instantánea. Cuando la partícula está bajo aceleración, cambia su velocidad cada segundo. Por lo tanto, no se puede asignar un solo valor a una velocidad. En tales casos, se prefiere la velocidad instantánea , que describe la velocidad y su dirección en un instante particular. está dado por,

$\vec{v} = \lim_{\Delta t \to 0}\frac{\Delta \vec{r}}{\Delta t}\\ = \vec{v} = \frac{dr}{dt}$

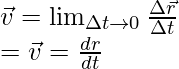
La velocidad también se puede expresar en forma de sus componentes.

$v = \frac{dx}{dt}\hat{i} + \frac{dy}{dt}\hat{j}$

La velocidad media es la relación entre el desplazamiento total y el tiempo total. Supongamos que una partícula va de $\vec{r}$ a $\vec{r'}$ en un tiempo total de $\Delta t$

La velocidad está dada por,

$\vec{v} = \frac{\vec{r} - \vec{r'}}{\Delta t}$

Aceleración

La aceleración de un cuerpo que se mueve en un plano está dada por la tasa de cambio en su velocidad. Similar a la velocidad, aquí también puede haber dos casos: aceleración promedio y aceleración instantánea. La aceleración promedio viene dada por la relación del cambio neto en la velocidad del objeto con el tiempo total empleado. Denotemos las velocidades inicial y final por $\vec{v}_{i}$ y $\vec{v_{f}}$

$\vec{v} = \frac{\vec{v_{f}} - \vec{v_{i}}}{\Delta t}$

La aceleración instantánea se usa cuando la aceleración del cuerpo cambia con el tiempo.

$\vec{a} = \lim_{\Delta t \to 0}\frac{\Delta \vec{v}}{\Delta t}\\ = \vec{a} = \frac{dv}{dt}$

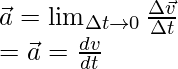
Esto también se puede descomponer en sus componentes.

$a = \frac{dv_{x}}{dt}\hat{i} + \frac{dv_{y}}{dt}\hat{j} \\ = a = \frac{d^2x}{dt^2}\hat{i} + \frac{d^2y}{dt^2}\hat{j}$

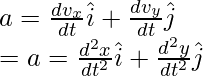
La magnitud de la aceleración también se puede calcular usando los componentes de la velocidad,

$a = \sqrt{a_x^2 + a_y^2}$

Y la dirección viene dada por el ángulo $\theta$ ,

$\theta = tan^{-1}(\frac{a_y}{a_x})$

Problemas de muestra

Pregunta 1: Encuentra la velocidad en t = 2, para la partícula que se mueve en un plano y cuya posición se da a continuación,

r = t ² yo + t ² j

Responder:

Dados: los vectores de posición inicial y final,

r = t ² yo + t ² j

El vector de posición cambia con el tiempo. La velocidad en este caso está dada por la fórmula,

$v = \frac{dx}{dt}\hat{i} + \frac{dy}{dt}\hat{j}$

Aquí x(t) = t ² y y(t) = t ²

Reemplazando estos valores en la ecuación,

$v = \frac{dx}{dt}\hat{i} + \frac{dy}{dt}\hat{j} \\ v= \frac{d}{dt}(t^2)\hat{i} + \frac{d}{dt}(t^2)\hat{j} \\ v = 2t \hat{i} + 2t\hat{j}$

En t = 2,

$v = 2t \hat{i} + 2t\hat{j} \\ = v = 2(2)\hat{i} + 2(2)\hat{j} \\ = v = 4\hat{i} + 4\hat{j}$

Pregunta 2: Encuentra la velocidad en t = 0, para la partícula que se mueve en un plano y cuya posición se da a continuación,

r = (t+2)i + (4t ² +2)j

Responder:

Dados: los vectores de posición inicial y final,

r = (t+2)i + (4t ² +2)j

El vector de posición cambia con el tiempo. La velocidad en este caso está dada por la fórmula,

$v = \frac{dx}{dt}\hat{i} + \frac{dy}{dt}\hat{j}$

Aquí x(t) = t+2 y y(t) = 4t ² +2

Reemplazando estos valores en la ecuación,

$v = \frac{dx}{dt}\hat{i} + \frac{dy}{dt}\hat{j} \\ v= \frac{d}{dt}(t+2)\hat{i} + \frac{d}{dt}(4t^2+2)\hat{j} \\ v = \hat{i} + 8t\hat{j}$

en t = 0,

$v = \hat{i} + 8t\hat{j} \\ = v = 4\hat{i} + 8(0)\hat{j} \\ = v = 4\hat{i}$

Pregunta 3: Encuentra la aceleración promedio entre t = 0 y t = 3, para la partícula que se mueve en un plano y cuya posición se da a continuación,

v = 3ti + 3t ^3j

Responder:

Dado: la velocidad en función del tiempo.

v = 3ti + 3t ^3j

El vector de velocidad cambia con el tiempo. La aceleración media viene dada por la fórmula,

$\vec{a} = \frac{\vec{v_f} - \vec{v_i}}{\Delta t}$

En t = 0

v _yo = 0i + 0j

En t = 3

v _f = 9i + 81j

$\Delta t = 3$

Reemplazando los valores en la ecuación anterior,

$\vec{a} = \frac{\vec{v_f} - \vec{v_i}}{\Delta t}\\ = \vec{a} = \frac{9\hat{i} + 81\hat{j}}{3} \\ = \vec{a} = 3\hat{i} + 27\hat{j}$

Pregunta 4: Encuentra la aceleración promedio entre t = 0 y t = 2, para la partícula que se mueve en un plano y cuya posición se da a continuación,

v = ti + 3tj

Responder:

Dado: la velocidad en función del tiempo.

v = ti + 3tj

El vector de velocidad cambia con el tiempo. La aceleración media viene dada por la fórmula,

$\vec{a} = \frac{\vec{v_f} - \vec{v_i}}{\Delta t}$

En t = 0

v _yo = 0i + 0j

En t = 2

v _f = 2i + 6j

$\Delta t = 2$

Reemplazando los valores en la ecuación anterior,

$\vec{a} = \frac{\vec{v_f} - \vec{v_i}}{\Delta t}\\ = \vec{a} = \frac{2\hat{i} + 6\hat{j}}{2} \\ = \vec{a} = \hat{i} + 3\hat{j}$

Pregunta 5: Encuentra la aceleración instantánea en t = 1, para la partícula que se mueve en un plano y cuya posición se da a continuación,

r = ti + tj

Responder:

Dados: los vectores de posición inicial y final,

r = ti + tj

El vector de posición cambia con el tiempo. La aceleración en términos de posición dada por,

$a = \frac{d^2x}{dt^2}\hat{i} + \frac{d^2y}{dt^2}\hat{j}$

x(t) = t y y(t) = t

Reemplazando los valores en la ecuación,

$a = \frac{d^2x}{dt^2}\hat{i} + \frac{d^2y}{dt^2}\hat{j} \\ a = \frac{d^2(t)}{dt^2}\hat{i} + \frac{d^2(t)}{dt^2}\hat{j} \\ a = 0\hat{i} + 0\hat{j}$

Pregunta 6: Encuentra la aceleración instantánea en t = 1, para la partícula que se mueve en un plano y cuya posición se da a continuación,

r = 3ti + t ³ j

Responder:

Dados: los vectores de posición inicial y final,

r = 3ti + t ³ j

El vector de posición cambia con el tiempo. La aceleración en términos de posición dada por,

$a = \frac{d^2x}{dt^2}\hat{i} + \frac{d^2y}{dt^2}\hat{j}$

x(t) = 3t y y(t) = t ³

Reemplazando los valores en la ecuación,

$a = \frac{d^2x}{dt^2}\hat{i} + \frac{d^2y}{dt^2}\hat{j} \\ a = \frac{d^2(3t)}{dt^2}\hat{i} + \frac{d^2(t^3)}{dt^2}\hat{j} \\ a = 0\hat{i} + 6t\hat{j}$

en t = 1

a = 6j

Pregunta 7: Un cuerpo se mueve en un plano 2D, su aceleración en el eje x es de 4 m/s ² y en el eje y es de 3 m/s ² . Encuentre la magnitud y el ángulo de la aceleración en el eje x.

Responder:

La magnitud de la aceleración también se puede calcular usando los componentes de la velocidad,

$a = \sqrt{a_x^2 + a_y^2}$

una _x = 4 m/s ² y una _y = 3 m/s ²

Reemplazando los valores en la ecuación,

$a = \sqrt{a_x^2 + a_y^2} \\ = a = \sqrt{3^2 + 4^2} \\ = a = \sqrt{9 + 16} \\ = a = \sqrt{25} \\ = a = 5$

El ángulo se puede calcular usando la ecuación,

$\theta = tan^{-1}(\frac{a_x}{a_y}) \\ \theta = tan^{-1}(\frac{3}{4})$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Movimiento en un plano

Problemas de muestra

Deja una respuesta Cancelar la respuesta