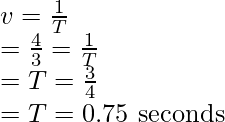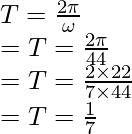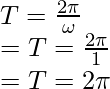Hay muchos tipos de movimientos que se encuentran en la vida diaria: el movimiento rectilíneo y el movimiento de un proyectil es uno de esos ejemplos. Ambos movimientos no son repetitivos. Significa que el objeto no vuelve al mismo lugar otra vez. Hay algunos movimientos que son de naturaleza repetitiva. Por ejemplo, el movimiento planetario. Todos los planetas se mueven alrededor del sol y completan revoluciones cada año. Este tipo de movimiento es el movimiento periódico. El estudio del movimiento periódico es una gran parte de la física, y es esencial saber cómo analizar dichos movimientos. Veamos estos movimientos en detalle.
Movimientos periódicos y oscilatorios
Considere el movimiento de un insecto que intenta escalar una pared. El insecto intenta trepar por una pared vertical, alcanza cierta altura y vuelve a caer. El insecto retrocede pero nuevamente intenta escalar la pared. La gráfica de la altura del insecto con el tiempo se muestra a continuación. En tal gráfico, observe que el insecto vuelve a cero una y otra vez. Este tipo de gráfico también se puede observar en una pelota que rebota. La pelota también vuelve a su posición en el suelo una y otra vez.
En el gráfico anterior, el movimiento se repite después de un cierto período de tiempo. Este tipo de movimiento se llama movimiento periódico . Ahora, dado que el objeto está cambiando su velocidad, eso significa que debe haber una fuerza que actúa sobre el objeto que lo devuelve a una determinada posición. Esa cierta posición se llama posición media . Cuando el cuerpo está en esta posición, ninguna fuerza actúa sobre él. Entonces, esta posición se llama posición de equilibrio .
La fuerza que trata de llevar el cuerpo a una posición de equilibrio da lugar al comportamiento repetitivo en el movimiento. Este comportamiento repetitivo también se denomina oscilaciones o vibraciones .
Nota: Realmente no hay mucha diferencia entre las oscilaciones y vibraciones. Cuando la frecuencia es pequeña, se denominan oscilaciones . De lo contrario, se llaman vibraciones .
Movimiento periódico
Considere el movimiento del reloj, las manecillas de las horas, las manecillas de los segundos y las manecillas de los minutos. Estas manecillas cubren todo el reloj y vuelven a la misma posición. En el movimiento periódico, un cuerpo parte de su posición de equilibrio y regresa a ella a intervalos iguales de tiempo. El movimiento circular es un ejemplo de movimiento periódico.
El movimiento periódico es diferente del movimiento oscilatorio. Por ejemplo, el movimiento circular es un movimiento periódico pero no es un movimiento oscilatorio. A continuación se dan algunos ejemplos de movimiento periódico:
- una mecedora
- una pelota que rebota
- Movimiento circular
Movimiento oscilatorio
El movimiento oscilatorio es el movimiento de los objetos hacia adelante y hacia atrás alrededor de una posición de equilibrio. Un péndulo oscilante es un ejemplo de movimiento oscilatorio. En la práctica, los cuerpos que realizan el movimiento del oscilador finalmente se detienen debido al amortiguamiento causado por fuerzas externas como la fricción o la presión del aire. Pero este tipo de movimiento se puede mantener usando una fuerza externa que mantenga un intervalo de tiempo igual. A continuación se dan algunos ejemplos de movimiento oscilatorio:
- Masa que realiza oscilaciones unida a un resorte.
- Un diapasón que realiza vibraciones.
- Un péndulo sencillo.
El movimiento armónico simple es el tipo más simple de movimiento oscilatorio.
El movimiento armónico simple (MAS) es un tipo de movimiento oscilatorio en el que la fuerza neta sobre el sistema restaura la fuerza que lo devuelve a una posición de equilibrio. Si la fuerza restauradora viene dada por F y el desplazamiento desde la posición media es x
Período y Frecuencia
Dado que el movimiento oscilatorio y el periódico se repiten después de intervalos de tiempo iguales. Hay ciertas cantidades medibles que nos permiten describir matemáticamente cualquier movimiento de este tipo. Tales cantidades también nos permiten describir el estado de cualquier objeto en movimiento periódico.
El intervalo más pequeño después de que un cuerpo repite su movimiento se llama Período de tiempo. Se denota por T. Su unidad SI es segundos. El recíproco del período de tiempo (T) se llama frecuencia. Se denota por f o v y su unidad SI es Hz. Indica el número de repeticiones por segundo.
v = 1 / T
Un desplazamiento se puede definir como la distancia del cuerpo oscilante desde la posición de equilibrio.
Una función periódica simple se puede escribir como,
f(t) = Asen(ωt)
El argumento ωt está dado por,
T = 2π / ω
Así, la función f(t) es periódica con T,
f(t + T) = f(t)
Problemas de muestra
Problema 1: Averigüe la frecuencia de un cuerpo en HM si el período de tiempo para el cuerpo es de 0,1 segundos.
Solución:
La frecuencia de un cuerpo está dada por,
v = 1 / T
donde v = frecuencia y T = período de tiempo.
Dado: T = 0,1 s
Reemplazando el valor en la ecuación,
v = 1 / 0,1 s
= 10 Hz.
Problema 2: Averigüe el período de tiempo de un cuerpo en SHM si la frecuencia del cuerpo es de 250 Hz.
Solución:
La frecuencia de un cuerpo está dada por,
v = 1 / T
donde, v = frecuencia y T = período de tiempo.
Dado: v = 250 Hz
Reemplazando el valor en la ecuación,
v = 1 / T
250 Hz = 1 / T
o
T = 0,004 s
Problema 3: El latido del corazón de una persona cuando se midió resultó ser 80 latidos por minuto. Encuentre el período de tiempo y la frecuencia.
Solución:
La frecuencia de un cuerpo viene dada por el número de veces que el corazón late por segundo.
v = 80 / 60
v = 1,33 latidos por segundo
La frecuencia está dada por,
v = 1 / T
donde v = frecuencia y T = período de tiempo.
Dado: v = 1,33 Hz
Reemplazando el valor en la ecuación,
Problema 4: Un cuerpo que realiza MAS se rige por la siguiente ecuación: A = 5sin(44t). Encuentra el período de tiempo.
Solución:
Una ecuación estándar de un SHM está dada por,
donde T = 2π / ω
En este caso, A = 5sen(44t)
Comparando las dos ecuaciones, encontramos que
ω = 44
Introducir el valor en la ecuación durante un período de tiempo.
Problema 5: Un cuerpo que realiza MAS se rige por la siguiente ecuación: A = 3sin(t). Encuentra el período de tiempo.
Solución:
Una ecuación estándar de un SHM está dada por,
Aquí,
En este caso, A = 3sen(t)
Comparando las dos ecuaciones, encontramos que
Introducir el valor en la ecuación durante un período de tiempo.
Problema 6: Un cuerpo que realiza MAS se rige por la siguiente ecuación: A = sen(t) + cos(t). Encuentra el período de tiempo.
Solución:
Una ecuación estándar de un SHM está dada por,
Aquí,
En este caso, A = sin(t) + cos(t)
Esta ecuación se puede reescribir como,
Comparando las dos ecuaciones, encontramos que
Introducir el valor en la ecuación durante un período de tiempo.
Publicación traducida automáticamente
Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA