Movimiento relativo

Posted on by Rudeus Greyrat

Si miras por la ventana de un tren en movimiento, verás que otro tren que está parado parece estar retrocediendo. ¿Qué hace que un tren inmóvil parezca moverse? Detrás hay una idea crucial llamada movimiento relativo, que nos ayudará a comprender por qué las cosas parecen moverse de manera diferente en diferentes marcos.

Para explicar el movimiento relativo en una o más dimensiones, se propuso originalmente la idea de marcos de referencia. Cuando decimos que un elemento tiene una velocidad específica, nos referimos a la velocidad con respecto a algún marco conocido como el marco de referencia. Cuando medimos la velocidad de un objeto en la vida cotidiana, usamos el suelo o la tierra como marco de referencia.

Movimiento en línea recta: también denominado movimiento lineal, el movimiento en línea recta se refiere al desplazamiento de un objeto con respecto al tiempo mientras el objeto se mueve a lo largo de una trayectoria recta. Es un movimiento unidimensional y puede expresarse bien usando solo el sistema de coordenadas del eje X. Por ejemplo, el automóvil que se mueve a lo largo del mismo camino como se muestra a continuación:

Movimiento relativo

El movimiento relativo se puede denominar como el movimiento de un objeto con respecto a algún otro objeto en reposo o en movimiento, es decir, un objeto en movimiento o estacionario. El movimiento del objeto no se calcula en referencia a la superficie de la tierra. 

La suposición al calcular el movimiento relativo es la comprensión de que el otro objeto está en un estado estático. El movimiento relativo abarca todos los aspectos del movimiento, es decir, velocidad, rapidez o aceleración. 

Si consideramos a una persona sentada en un avión, la persona parece tener una velocidad cero en relación con el avión, pero en realidad se mueve con la misma velocidad que la del avión teniendo en cuenta el suelo. En este movimiento, depende de lo observado por el observador, depende del marco de referencia del observador. Los objetos pueden estar moviéndose en la misma dirección o en direcciones diferentes con referencia a los demás. 

Velocidad relativa

La velocidad relativa del cuerpo entra en consideración cuando el otro objeto se mueve en la misma dirección o en dirección opuesta. Las velocidades de los objetos involucrados pueden ser crecientes, decrecientes o constantes entre sí. 

Supongamos que la posición inicial de dos objetos A y B están ambos en el origen, en los puntos x A (0) y x B (0) respectivamente. Las posiciones correspondientes de estos objetos en la instancia de tiempo t serán equivalentes a,

x UN (t) = x UN (0) + v UN t

x segundo (t) = x segundo (0) + v segundo t

El desplazamiento del objeto A al B está dado por, 

[x B (0) – x A (0)] + (v B -v A )t

La velocidad de B relativa a A está dada por, 

v BA = v B – v A

La velocidad de A relativa a B está dada por, 

v AB = v A – v B

Gráficos PT que representan velocidades relativas

  • Dos objetos que se mueven en la misma dirección con velocidades iguales.

V segundo = V UN , V BA = V AB = 0

  • Dos objetos visiblemente estacionarios el uno para el otro.

V A > V B , V BA = -V AB

  • La magnitud de V BA y V AB será menor que la magnitud de V A y V B . El objeto A aparece más rápido que el B.

V A y V B de signo opuesto: V BA = -V AB

  • La magnitud de V BA y V AB será mayor que la magnitud de V A y V B . Ambos objetos aparecerán moviéndose más rápido el uno al otro.

Marcos de referencia

La velocidad de un objeto siempre se considera con referencia a un marco de tiempo y referencia (posición). El objeto toma una velocidad uniforme con un marco de referencia particularmente visible. El marco de referencia se considera la superficie de la tierra para todos los efectos prácticos. 

Por ejemplo, considerando el movimiento de los objetos, se supone que la superficie de la tierra es el marco de referencia y todo el movimiento se considera con referencia a este punto estático. Los objetos pueden estar en la misma dirección o en direcciones opuestas. El movimiento relativo se puede considerar a lo largo de una línea recta o en un plano, en múltiples dimensiones. 

Movimiento relativo en una dimensión

La velocidad de un objeto se puede considerar en cualquiera de las dos direcciones, igual u opuesta. Pueden presentarse los siguientes casos: 

  • Los objetos pueden estar moviéndose en la misma dirección con referencia a los demás. 

Si el objeto y la persona se mueven en la misma dirección, por ejemplo, un tren y una persona con la superficie de la Tierra como marco de referencia. La velocidad del tren con respecto a la Tierra se puede escribir como:

\vec{v}_{TE}=v \space m/s\ \hat{i}

Esta velocidad puede considerarse positiva. 

  • Los objetos pueden moverse en direcciones opuestas entre sí. 

Si el objeto y la persona se mueven en la misma dirección, por ejemplo, un tren y una persona retroceden hacia la estación con la superficie de la Tierra como marco de referencia. La velocidad de un tren con respecto a la Tierra se puede escribir como; 

\vec{v}_{PT}=-v \space m/s\ \hat{i}

Esta velocidad puede considerarse negativa.  

La suma de los vectores de velocidad se puede calcular para encontrar la velocidad de la persona con respecto a la Tierra. La velocidad relativa viene dada por, 

\vec{v}_{PE}=\vec{v}_{PT}+\vec{v}_{TE}

El orden de los subíndices se puede organizar para adaptarse a los requisitos. Durante la construcción de la ecuación vectorial, los subíndices del marco de referencia de acoplamiento aparecen consecutivamente hacia el marco de referencia interno. 

Figura 1

Supongamos que la primera velocidad de los objetos que se mueven en la misma dirección es de 10 m/s. En el segundo caso, la velocidad de la persona que se desplaza en sentido contrario al del tren, será de -2 m/s. Sumando los vectores, encontramos,

\vec{v}_{PE}=8m/s\ \hat{i}  

lleva a la conclusión de que la persona se mueve 8 m/s hacia el este con respecto a la Tierra. Vectores de velocidad del tren con respecto a la Tierra, de la persona con respecto al tren y de la persona con respecto a la Tierra.

Figura 2

Movimiento relativo en dos dimensiones

Consideremos dos objetos, P y Q, cada uno de ellos viajando con velocidades uniformes, v 1 y v 2 respectivamente. El movimiento de los objetos se considera paralelo entre sí en la misma dirección. La instancia de tiempo de inicio fue 0, en el origen. Supongamos sus desplazamientos desde el origen X 01 y X 02 en algún otro momento.

En el tiempo ‘t’: Los desplazamientos se vuelven x 1 y x 2 con respecto al origen con el eje de posición, la posición del objeto P en una instancia de tiempo particular se vuelve:

x 1 = x 01 + v 1 t …….(1)

Del mismo modo, para el objeto Q: 

x2 = x02 + v2t …….(2 )

Igualando las ecuaciones. 

Restando la ecuación (1) de (2), obtenemos:

(x 2 – x 1 ) = (x 02 – x 01 ) + (v 2 – v 1 )t …….(3)

Tenemos, x 01 y x 02 son los desplazamientos iniciales del objeto Q con respecto al objeto P en el instante de tiempo ‘t = 0’, por lo que la ecuación se reduce a:

x0 = x02 – x01 ……   (4)

Al sustituir el valor de la ecuación (4) en (3), obtenemos:

(x 2 – x 1 ) = x 0 + (v 2 -v 1 )t …….(5)

Si igualamos las ecuaciones, (x 2 – x 1 ) es el desplazamiento relativo del objeto Q en referencia a las coordenadas posicionales del objeto P, en el instante de tiempo de t segundos. Usando esto, obtenemos, 

x = x 0 + (v Q – v P )t …….(6) [ Reescribiendo la ecuación. (5) ]

También, 

\frac{x-x_0}{t}=(v_2-v_1)\ \ \ \ .........(7)    ……(7)

Así, obtenemos que la velocidad es la razón de cambio del desplazamiento. 

  • Velocidad relativa para objetos que se mueven en la misma dirección

Usando (7), derivando la velocidad relativa del objeto Q con respecto al objeto P, mientras se mueve en la misma dirección. 

v QP = v 2 – v 1   …..(8)

  • Velocidad relativa para objetos que se mueven en la dirección opuesta

Usando (7), derivando la velocidad relativa del objeto Q con respecto al objeto P, mientras se mueve en la dirección opuesta.  

v QP = v 2 + v 1   ……(9)

La dimensión de la velocidad relativa es la misma que la de la velocidad, la cual viene dada por [M 0 L 1 T -1 ]. 

Problemas de muestra

Problema 1: Los atletas participan en una carrera de relevos en la pista, corriendo con velocidades respectivas de  \vec v_c y  \vec v_{rel}. Calcular la velocidad relativa. 

Solución:

\vec v=\vec vrel-\vec vc

Ahora, si ella se mueve en la dirección opuesta, entonces la ecuación será:

\vec v=\vec vrel+\vec vc

Problema 2: Considere un satélite que se mueve a lo largo del plano ecuatorial con una velocidad de sm/s. ¿Encuentra la velocidad relativa del satélite correspondiente con respecto al punto de referencia que es la superficie de la tierra?

Solución:

\vec v_{se}=\vec v_s-\vec v_e

Considere que el satélite se mueve en la dirección de rotación de la tierra sobre su eje, por lo tanto, la velocidad se convierte en:

v_{se}=v_s-v_e

Problema 3: El ascensor se mueve hacia arriba con una aceleración uniforme ‘a’ m/s 2 . El hombre lanza una pelota de goma hacia arriba con una velocidad v relativa al ascensor. El hombre atrapa la pelota después de un tiempo de t segundos. Demuestre que a + g = 2v/t.

Solución:

Se puede suponer que el marco del ascensor es el punto de referencia. Por lo tanto, los aspectos de movimiento, aceleración, desplazamiento y velocidad se considerarán desde el punto de referencia. Cuando la pelota regresa al hombre, por lo tanto, el desplazamiento desde el marco del ascensor se vuelve cero. Supongamos que la velocidad del objeto con respecto al marco del ascensor es v.

g – (-a) = a + g (↓) hacia abajo

Ahora, s = ut + \frac{1}{2}a^2    

⇒ 0 = vt - \frac{1}{2} (a+g)t^2

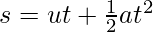
o  

un + gramo = 2 (v/t) .

Problema 4: Los dos trenes se mueven con velocidades diferentes, t 1 con 10 m/sy t 2 con 15 m/s en vías paralelas con referencia a la otra. Calcule la velocidad relativa del tren t 1 con respecto a t 2 .

Solución: 

Dado, 

v 1 = 10 ms -1 , v 2 = 15 ms -1

Velocidad relativa del tren lento con respecto al tren rápido = v 1 – v 2 = 10 – 15 = – 5 ms -1 

El signo negativo muestra que el tren lento parece moverse hacia el oeste con respecto al tren rápido con una velocidad de 5 ms- 1 .

Problema 5: El carro A se mueve con una velocidad de 40 ms -1 de Norte a Sur a lo largo de una pista, mientras que el carro B se mueve en dirección opuesta a la tarjeta anterior con una velocidad de 30 ms -1 de Sur a Norte. Calcule las velocidades relativas de ambos carros entre sí. 

Solución: 

Consideremos positiva la dirección de norte a sur.

Por lo tanto,

v A = +40 ms -1 y v B = -30 ms -1

(i) Velocidad relativa de B wrt A = v B – v A = -30 – 40 = – 70 ms -1 

Por lo tanto, el carro B parece moverse de Sur a Norte con una velocidad de 70 ms -1 para cualquier persona sentada en el carro A.

(ii) Velocidad del suelo, v B = 0, ya que es un objeto estacionario. 

Velocidad relativa del suelo w.rt. A = v B – v A = 0 – 40 = – 40 ms -1 

Por lo tanto, el suelo parece moverse de sur a norte con una velocidad de 40 ms -1 wrt cart A.

Publicación traducida automáticamente

Artículo escrito por codersgram9 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *