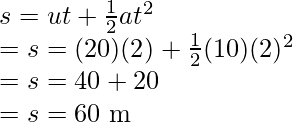Movimiento uniformemente acelerado

Cuando un cuerpo se mueve en un plano o en línea recta, se utilizan tres parámetros para describir su movimiento: distancia, velocidad y aceleración. La distancia o el desplazamiento se explican por sí mismos. La velocidad representa la tasa de cambio de posición, mientras que la aceleración representa la tasa de cambio de velocidad. Las tres cantidades son cantidades vectoriales. La aceleración puede ser uniforme o no uniforme. Una aceleración uniforme tiene un valor y una dirección constantes. Es esencial conocer la ecuación de movimientos que describen el movimiento de un objeto bajo una aceleración uniforme. Veámoslos en detalle.

Aceleración

La aceleración se define como la tasa de cambio del vector de velocidad. La aceleración puede ser constante o variable. En el caso de aceleración constante, su valor viene dado por la relación entre el cambio neto de velocidad y el tiempo total empleado. También se le llama aceleración media. En los casos en que la aceleración varía con el tiempo, se calcula la aceleración instantánea.

Aceleración media:

$\vec{a} = \frac{\vec{v_f} - \vec{v_i}}{\Delta t}$

Aceleración instantánea:

$\vec{a} = \frac{d\vec{v}}{dt} \\ = \vec{a} = \frac{dx}{dx}\hat{i} + \frac{dy}{dt}\hat{j}$

Aceleración uniforme

La aceleración uniforme es la aceleración que no varía con el tiempo. En tales casos, la tasa de cambio de la velocidad permanece constante. Dado que la aceleración es una cantidad vectorial, incluso la dirección del movimiento permanece igual en el caso de una aceleración constante. Dado que el cuerpo se mueve en una sola dirección con una magnitud constante de aceleración, se pueden descartar las notaciones vectoriales.

Algunos ejemplos de aceleración constante incluyen

Objeto en caída libre.
Una pelota que rueda por una pendiente sin fricción.
Una bicicleta cuyos frenos han sido accionados.

Ecuaciones de movimiento uniformemente acelerado

En este caso, manteniendo constante el valor de la aceleración. Se pueden describir ecuaciones de movimiento. Digamos que la velocidad inicial de un objeto era “u”, ahora se aplica una fuerza constante que hace que el cuerpo se mueva con aceleración constante “a” y el cuerpo alcanza la velocidad en el tiempo “t” mientras recorre la distancia “s”.

Primera ecuación de movimiento

En el caso de aceleración constante, su valor viene dado por,

$a = \frac{v - u}{t} \\ =at = v - u \\ =v = u + at$

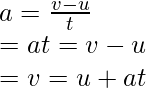
Segunda ecuación de movimiento

La velocidad instantánea está dada por,

$v = \frac{ds}{dt}$

Esta ecuación se puede reorganizar de la siguiente forma,

ds = vdt

Sustituyendo el valor de la velocidad de la ecuación anterior,

ds = (u + en)dt

Integrando ambos lados,

$\int^{s_2}_{0}ds = \int^{t}_{0}(u + at)dt \\ s = \int^{t}_{0}udt + \int^{t}_{0}atdt \\ s = u[t]^{t}_{0} + a[\frac{t^2}{2}]^{t}_{0} \\ s= ut + \frac{1}{2}at^2$

Tercera ecuación de movimiento

La aceleración instantánea y la velocidad instantánea están dadas por,

un = $\frac{dv}{dt}$

v = $\frac{ds}{dt}$

Multiplicando en cruz ambas ecuaciones,

$a\frac{ds}{dt} = v\frac{dv}{dt} \\ = \int^{s}_{0}a\frac{ds}{dt} = \int^{v}_{u}v\frac{dv}{dt} \\ = as = [\frac{v^2}{2}]^{v}_{u} \\ = as = \frac{v^2 - u^2}{2} \\ = 2as =v^2 - u^2$

v ² = tu ² + 2 como

Problemas de muestra

Pregunta 1: Si un cuerpo se mueve con una aceleración de 2 m/s ² . Si la velocidad inicial era de 15 m/s, ¿cuál será la velocidad en 5 segundos?

Responder:

Sea u la velocidad inicial y v la velocidad final.

Dado: u = 15 m/s, a = 2 m/s ² y t = 5

Para averiguar el valor de «v», se puede usar la primera ecuación de movimiento.

v = tu + en

Reemplazando los valores en esta ecuación,

v = tu + en

⇒ v = 15 + (2)(5)

⇒ v = 15 + 10

⇒ v = 25 m/s

Pregunta 2: Si un cuerpo se mueve con una aceleración de -5 m/s ² . Si la velocidad inicial era de 30 m/s, ¿cuál será la distancia co en 5 segundos?

Responder:

Sea u la velocidad inicial y v la velocidad final.

Dado: u = 40 m/s, a = -5 m/s ² y t = 5

Para averiguar el valor de «v», se puede usar la primera ecuación de movimiento.

v = tu + en

Reemplazando los valores en esta ecuación,

v = tu + en

⇒ v = 30 – (5)(5)

⇒ v = 30 – 25

⇒ v = 5 m/s

Pregunta 3: Si un cuerpo se mueve con una aceleración de -5 m/s ² . Si la velocidad inicial era de 40 m/s, ¿cuál será la velocidad en 5 segundos?

Responder:

Sea u la velocidad inicial

Dado: u = 40 m/s, a = -5 m/s ² y t = 5

Para averiguar el valor de «s», se puede usar la primera ecuación de movimiento.

$s= ut + \frac{1}{2}at^2$

Reemplazando los valores en esta ecuación,

$s= ut + \frac{1}{2}at^2 \\ = s = (40)(5) + \frac{1}{2}(-5)(5)^2 \\ = s = 200 + \frac{1}{2}(-125) \\ = s = \frac{400 - 125}{2} \\ = s= \frac{275}{2} \text{ m}$

Pregunta 4: Si un cuerpo se mueve con una aceleración de 10 m/s ² . Si la velocidad inicial era de 20 m/s, ¿cuál será la velocidad en 2 segundos?

Responder:

Sea u la velocidad inicial

Dado: u = 20 m/s, a = 10 m/s ² y t = 2

Para averiguar el valor de «s», se puede usar la primera ecuación de movimiento.

$s= ut + \frac{1}{2}at^2$

Reemplazando los valores en esta ecuación,

$s= ut + \frac{1}{2}at^2 \\ = s = (20)(2) + \frac{1}{2}(10)(2)^2 \\ = s = 40 + 20 \\ = s= 60 \text{ m}$

Pregunta 5: Un coche de carreras alcanza una velocidad de 20 m/s en 2 segundos. Encuentre la distancia recorrida por el automóvil en el proceso.

Responder:

Sea u la velocidad inicial y v la velocidad final.

Dado: u = 0 m/s, v = 20 m/s y t = 2.

Para averiguar el valor de «a», se puede utilizar la primera ecuación de movimiento.

v = tu + en

Reemplazando los valores en esta ecuación,

v = tu + en

⇒ 20 = 0 + (a)(2)

⇒ 20 = 2a

⇒ a = 10 m/s ²

Para averiguar la distancia, se utilizará una tercera ecuación de movimiento.

v ² = tu ² + 2 como

⇒ 20 ² = 0 + 2(10)s

⇒ 400 = 20 s

⇒20m = s

Pregunta 6: Un cohete alcanza una velocidad de 50 m/s en 5 segundos. Encuentre la distancia recorrida por el cohete en el proceso.

Responder:

Sea u la velocidad inicial y v la velocidad final.

Dado: u = 0 m/s, v = 50 m/s y t = 5.

Para averiguar el valor de «a», se puede utilizar la primera ecuación de movimiento.

v = tu + en

Reemplazando los valores en esta ecuación,

v = tu + en

⇒ 50 =0 + (a)(5)

⇒ 50 = 5a

⇒ a = 10 m/s ²

Para averiguar la distancia, se utilizará una tercera ecuación de movimiento.

v ² = tu ² + 2 como

⇒ 50 ² = 0 + 2(10)s

⇒ 2500 = 20 s

⇒125m = s

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Aceleración

Aceleración uniforme

Ecuaciones de movimiento uniformemente acelerado

Problemas de muestra

Deja una respuesta Cancelar la respuesta