Recomendamos leer las siguientes dos publicaciones como requisito previo para esta publicación.
- Algoritmos codiciosos | Conjunto 5 (Árbol de expansión mínimo (MST) de Prim)
- Gráfico y sus representaciones
Hemos discutido el algoritmo de Prim y su implementación para la representación de gráficos de array de adyacencia . La complejidad temporal para la representación matricial es O(V^2). En esta publicación, se analiza el algoritmo O(ELogV) para la representación de listas de adyacencia.
Como se discutió en la publicación anterior, en el algoritmo de Prim, se mantienen dos conjuntos, un conjunto contiene una lista de vértices ya incluidos en MST, otro conjunto contiene vértices aún no incluidos. Con la representación de lista de adyacencia, todos los vértices de un gráfico se pueden recorrer en tiempo O(V+E) usando BFS . La idea es atravesar todos los vértices del gráfico usando BFS y usar un Min Heap para almacenar los vértices que aún no están incluidos en MST. Min Heap se utiliza como cola de prioridad para obtener el margen de peso mínimo del corte . Min Heap se usa como complejidad de tiempo de operaciones como extraer el elemento mínimo y el valor clave decreciente es O (LogV) en Min Heap.
Los siguientes son los pasos detallados.
- Cree un Min Heap de tamaño V donde V es el número de vértices en el gráfico dado. Cada Node del montón mínimo contiene el número de vértice y el valor clave del vértice.
- Inicialice Min Heap con el primer vértice como raíz (el valor clave asignado al primer vértice es 0). El valor clave asignado a todos los demás vértices es INF (infinito).
- Mientras Min Heap no está vacío, haga lo siguiente
- Extraiga el Node de valor mínimo de Min Heap. Sea u el vértice extraído.
- Para cada vértice adyacente v de u, verifique si v está en Min Heap (aún no incluido en MST). Si v está en Min Heap y su valor clave es mayor que el peso de uv, actualice el valor clave de v como peso de uv.
Entendamos el algoritmo anterior con el siguiente ejemplo:
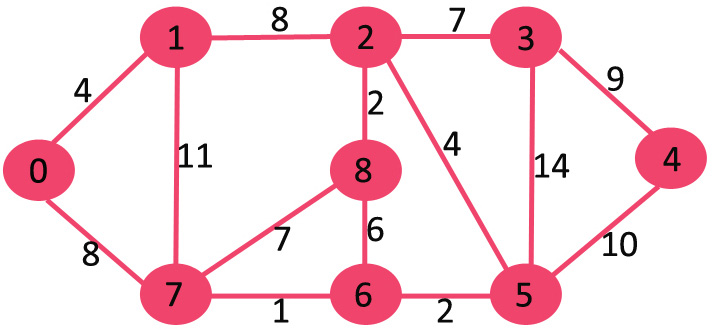
Inicialmente, el valor clave del primer vértice es 0 e INF (infinito) para todos los demás vértices. Entonces, el vértice 0 se extrae de Min Heap y los valores clave de los vértices adyacentes a 0 (1 y 7) se actualizan. Min Heap contiene todos los vértices excepto el vértice 0.
Los vértices en color verde son los vértices incluidos en MST.
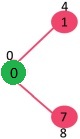
Dado que el valor clave del vértice 1 es mínimo entre todos los Nodes en Min Heap, se extrae de Min Heap y los valores clave de los vértices adyacentes a 1 se actualizan (la clave se actualiza si un vértice está en Min Heap y el valor de clave anterior es mayor que el peso del borde de 1 al adyacente). Min Heap contiene todos los vértices excepto los vértices 0 y 1.
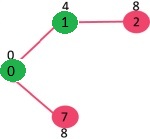
Dado que el valor clave del vértice 7 es mínimo entre todos los Nodes en Min Heap, se extrae de Min Heap y los valores clave de los vértices adyacentes a 7 se actualizan (la clave se actualiza si un vértice está en Min Heap y el valor de clave anterior es mayor que el peso del borde de 7 al adyacente). Min Heap contiene todos los vértices excepto los vértices 0, 1 y 7.
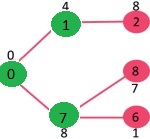
Dado que el valor clave del vértice 6 es mínimo entre todos los Nodes en Min Heap, se extrae de Min Heap y los valores clave de los vértices adyacentes a 6 se actualizan (la clave se actualiza si un vértice está en Min Heap y el valor de clave anterior es mayor que el peso del borde de 6 al adyacente). Min Heap contiene todos los vértices excepto los vértices 0, 1, 7 y 6.
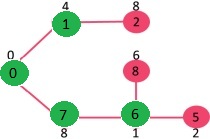
Los pasos anteriores se repiten para el resto de los Nodes en Min Heap hasta que Min Heap se vacía
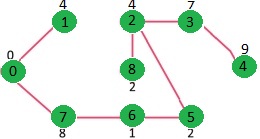
Implementación:
C++
// C / C++ program for Prim's MST for adjacency list
// representation of graph
#include <limits.h>
#include <stdio.h>
#include <stdlib.h>
// A structure to represent a node in adjacency list
struct AdjListNode {
int dest;
int weight;
struct AdjListNode* next;
};
// A structure to represent an adjacency list
struct AdjList {
struct AdjListNode*
head; // pointer to head node of list
};
// A structure to represent a graph. A graph is an array of
// adjacency lists. Size of array will be V (number of
// vertices in graph)
struct Graph {
int V;
struct AdjList* array;
};
// A utility function to create a new adjacency list node
struct AdjListNode* newAdjListNode(int dest, int weight)
{
struct AdjListNode* newNode
= (struct AdjListNode*)malloc(
sizeof(struct AdjListNode));
newNode->dest = dest;
newNode->weight = weight;
newNode->next = NULL;
return newNode;
}
// A utility function that creates a graph of V vertices
struct Graph* createGraph(int V)
{
struct Graph* graph
= (struct Graph*)malloc(sizeof(struct Graph));
graph->V = V;
// Create an array of adjacency lists. Size of array
// will be V
graph->array = (struct AdjList*)malloc(
V * sizeof(struct AdjList));
// Initialize each adjacency list as empty by making
// head as NULL
for (int i = 0; i < V; ++i)
graph->array[i].head = NULL;
return graph;
}
// Adds an edge to an undirected graph
void addEdge(struct Graph* graph, int src, int dest,
int weight)
{
// Add an edge from src to dest. A new node is added to
// the adjacency list of src. The node is added at the
// beginning
struct AdjListNode* newNode
= newAdjListNode(dest, weight);
newNode->next = graph->array[src].head;
graph->array[src].head = newNode;
// Since graph is undirected, add an edge from dest to
// src also
newNode = newAdjListNode(src, weight);
newNode->next = graph->array[dest].head;
graph->array[dest].head = newNode;
}
// Structure to represent a min heap node
struct MinHeapNode {
int v;
int key;
};
// Structure to represent a min heap
struct MinHeap {
int size; // Number of heap nodes present currently
int capacity; // Capacity of min heap
int* pos; // This is needed for decreaseKey()
struct MinHeapNode** array;
};
// A utility function to create a new Min Heap Node
struct MinHeapNode* newMinHeapNode(int v, int key)
{
struct MinHeapNode* minHeapNode
= (struct MinHeapNode*)malloc(
sizeof(struct MinHeapNode));
minHeapNode->v = v;
minHeapNode->key = key;
return minHeapNode;
}
// A utilit function to create a Min Heap
struct MinHeap* createMinHeap(int capacity)
{
struct MinHeap* minHeap
= (struct MinHeap*)malloc(sizeof(struct MinHeap));
minHeap->pos = (int*)malloc(capacity * sizeof(int));
minHeap->size = 0;
minHeap->capacity = capacity;
minHeap->array = (struct MinHeapNode**)malloc(
capacity * sizeof(struct MinHeapNode*));
return minHeap;
}
// A utility function to swap two nodes of min heap. Needed
// for min heapify
void swapMinHeapNode(struct MinHeapNode** a,
struct MinHeapNode** b)
{
struct MinHeapNode* t = *a;
*a = *b;
*b = t;
}
// A standard function to heapify at given idx
// This function also updates position of nodes when they
// are swapped. Position is needed for decreaseKey()
void minHeapify(struct MinHeap* minHeap, int idx)
{
int smallest, left, right;
smallest = idx;
left = 2 * idx + 1;
right = 2 * idx + 2;
if (left < minHeap->size
&& minHeap->array[left]->key
< minHeap->array[smallest]->key)
smallest = left;
if (right < minHeap->size
&& minHeap->array[right]->key
< minHeap->array[smallest]->key)
smallest = right;
if (smallest != idx) {
// The nodes to be swapped in min heap
MinHeapNode* smallestNode
= minHeap->array[smallest];
MinHeapNode* idxNode = minHeap->array[idx];
// Swap positions
minHeap->pos[smallestNode->v] = idx;
minHeap->pos[idxNode->v] = smallest;
// Swap nodes
swapMinHeapNode(&minHeap->array[smallest],
&minHeap->array[idx]);
minHeapify(minHeap, smallest);
}
}
// A utility function to check if the given minHeap is ampty
// or not
int isEmpty(struct MinHeap* minHeap)
{
return minHeap->size == 0;
}
// Standard function to extract minimum node from heap
struct MinHeapNode* extractMin(struct MinHeap* minHeap)
{
if (isEmpty(minHeap))
return NULL;
// Store the root node
struct MinHeapNode* root = minHeap->array[0];
// Replace root node with last node
struct MinHeapNode* lastNode
= minHeap->array[minHeap->size - 1];
minHeap->array[0] = lastNode;
// Update position of last node
minHeap->pos[root->v] = minHeap->size - 1;
minHeap->pos[lastNode->v] = 0;
// Reduce heap size and heapify root
--minHeap->size;
minHeapify(minHeap, 0);
return root;
}
// Function to decrease key value of a given vertex v. This
// function uses pos[] of min heap to get the current index
// of node in min heap
void decreaseKey(struct MinHeap* minHeap, int v, int key)
{
// Get the index of v in heap array
int i = minHeap->pos[v];
// Get the node and update its key value
minHeap->array[i]->key = key;
// Travel up while the complete tree is not hepified.
// This is a O(Logn) loop
while (i
&& minHeap->array[i]->key
< minHeap->array[(i - 1) / 2]->key) {
// Swap this node with its parent
minHeap->pos[minHeap->array[i]->v] = (i - 1) / 2;
minHeap->pos[minHeap->array[(i - 1) / 2]->v] = i;
swapMinHeapNode(&minHeap->array[i],
&minHeap->array[(i - 1) / 2]);
// move to parent index
i = (i - 1) / 2;
}
}
// A utility function to check if a given vertex
// 'v' is in min heap or not
bool isInMinHeap(struct MinHeap* minHeap, int v)
{
if (minHeap->pos[v] < minHeap->size)
return true;
return false;
}
// A utility function used to print the constructed MST
void printArr(int arr[], int n)
{
for (int i = 1; i < n; ++i)
printf("%d - %d\n", arr[i], i);
}
// The main function that constructs Minimum Spanning Tree
// (MST) using Prim's algorithm
void PrimMST(struct Graph* graph)
{
int V = graph->V; // Get the number of vertices in graph
int parent[V]; // Array to store constructed MST
int key[V]; // Key values used to pick minimum weight
// edge in cut
// minHeap represents set E
struct MinHeap* minHeap = createMinHeap(V);
// Initialize min heap with all vertices. Key value of
// all vertices (except 0th vertex) is initially
// infinite
for (int v = 1; v < V; ++v) {
parent[v] = -1;
key[v] = INT_MAX;
minHeap->array[v] = newMinHeapNode(v, key[v]);
minHeap->pos[v] = v;
}
// Make key value of 0th vertex as 0 so that it
// is extracted first
key[0] = 0;
minHeap->array[0] = newMinHeapNode(0, key[0]);
minHeap->pos[0] = 0;
// Initially size of min heap is equal to V
minHeap->size = V;
// In the following loop, min heap contains all nodes
// not yet added to MST.
while (!isEmpty(minHeap)) {
// Extract the vertex with minimum key value
struct MinHeapNode* minHeapNode
= extractMin(minHeap);
int u
= minHeapNode
->v; // Store the extracted vertex number
// Traverse through all adjacent vertices of u (the
// extracted vertex) and update their key values
struct AdjListNode* pCrawl = graph->array[u].head;
while (pCrawl != NULL) {
int v = pCrawl->dest;
// If v is not yet included in MST and weight of
// u-v is less than key value of v, then update
// key value and parent of v
if (isInMinHeap(minHeap, v)
&& pCrawl->weight < key[v]) {
key[v] = pCrawl->weight;
parent[v] = u;
decreaseKey(minHeap, v, key[v]);
}
pCrawl = pCrawl->next;
}
}
// print edges of MST
printArr(parent, V);
}
// Driver program to test above functions
int main()
{
// Let us create the graph given in above fugure
int V = 9;
struct Graph* graph = createGraph(V);
addEdge(graph, 0, 1, 4);
addEdge(graph, 0, 7, 8);
addEdge(graph, 1, 2, 8);
addEdge(graph, 1, 7, 11);
addEdge(graph, 2, 3, 7);
addEdge(graph, 2, 8, 2);
addEdge(graph, 2, 5, 4);
addEdge(graph, 3, 4, 9);
addEdge(graph, 3, 5, 14);
addEdge(graph, 4, 5, 10);
addEdge(graph, 5, 6, 2);
addEdge(graph, 6, 7, 1);
addEdge(graph, 6, 8, 6);
addEdge(graph, 7, 8, 7);
PrimMST(graph);
return 0;
}
Java
// Java program for Prim's MST for
// adjacency list representation of graph
import java.util.Comparator;
import java.util.LinkedList;
import java.util.TreeSet;
public class prims {
class node1 {
// Stores destination vertex in adjacency list
int dest;
// Stores weight of a vertex in the adjacency list
int weight;
// Constructor
node1(int a, int b)
{
dest = a;
weight = b;
}
}
static class Graph {
// Number of vertices in the graph
int V;
// List of adjacent nodes of a given vertex
LinkedList<node1>[] adj;
// Constructor
Graph(int e)
{
V = e;
adj = new LinkedList[V];
for (int o = 0; o < V; o++)
adj[o] = new LinkedList<>();
}
}
// class to represent a node in PriorityQueue
// Stores a vertex and its corresponding
// key value
class node {
int vertex;
int key;
}
// Comparator class created for PriorityQueue
// returns 1 if node0.key > node1.key
// returns 0 if node0.key < node1.key and
// returns -1 otherwise
// in case two verties with equal weights are connected to a vertex then we compare the vertex for sorting
class comparator implements Comparator<node> {
@Override public int compare(node node0, node node1)
{
return node0.key != node1.key ? node0.key - node1.key : node0.vertex - node1.vertex;
}
}
// method to add an edge
// between two vertices
void addEdge(Graph graph, int src, int dest, int weight)
{
node1 node0 = new node1(dest, weight);
node1 node = new node1(src, weight);
graph.adj[src].addLast(node0);
graph.adj[dest].addLast(node);
}
// method used to find the mst
void prims_mst(Graph graph)
{
// Whether a vertex is in PriorityQueue or not
Boolean[] mstset = new Boolean[graph.V];
node[] e = new node[graph.V];
// Stores the parents of a vertex
int[] parent = new int[graph.V];
for (int o = 0; o < graph.V; o++)
e[o] = new node();
for (int o = 0; o < graph.V; o++) {
// Initialize to false
mstset[o] = false;
// Initialize key values to infinity
e[o].key = Integer.MAX_VALUE;
e[o].vertex = o;
parent[o] = -1;
}
// Include the source vertex in mstset
mstset[0] = true;
// Set key value to 0
// so that it is extracted first
// out of PriorityQueue
e[0].key = 0;
// Use TreeSet instead of PriorityQueue as the
// remove function of the PQ is O(n) in java.
TreeSet<node> queue
= new TreeSet<node>(new comparator());
for (int o = 0; o < graph.V; o++)
queue.add(e[o]);
// Loops until the queue is not empty
while (!queue.isEmpty()) {
// Extracts a node with min key value
node node0 = queue.pollFirst();
// Include that node into mstset
mstset[node0.vertex] = true;
// For all adjacent vertex of the extracted
// vertex V
for (node1 iterator : graph.adj[node0.vertex]) {
// If V is in queue
if (mstset[iterator.dest] == false) {
// If the key value of the adjacent
// vertex is more than the extracted key
// update the key value of adjacent
// vertex to update first remove and add
// the updated vertex
if (e[iterator.dest].key
> iterator.weight) {
queue.remove(e[iterator.dest]);
e[iterator.dest].key
= iterator.weight;
queue.add(e[iterator.dest]);
parent[iterator.dest]
= node0.vertex;
}
}
}
}
// Prints the vertex pair of mst
for (int o = 1; o < graph.V; o++)
System.out.println(parent[o] + " "
+ "-"
+ " " + o);
}
public static void main(String[] args)
{
int V = 9;
Graph graph = new Graph(V);
prims e = new prims();
e.addEdge(graph, 0, 1, 4);
e.addEdge(graph, 0, 7, 8);
e.addEdge(graph, 1, 2, 8);
e.addEdge(graph, 1, 7, 11);
e.addEdge(graph, 2, 3, 7);
e.addEdge(graph, 2, 8, 2);
e.addEdge(graph, 2, 5, 4);
e.addEdge(graph, 3, 4, 9);
e.addEdge(graph, 3, 5, 14);
e.addEdge(graph, 4, 5, 10);
e.addEdge(graph, 5, 6, 2);
e.addEdge(graph, 6, 7, 1);
e.addEdge(graph, 6, 8, 6);
e.addEdge(graph, 7, 8, 7);
// Method invoked
e.prims_mst(graph);
}
}
// This code is contributed by Vikash Kumar Dubey
Python3
# A Python program for Prims's MST for
# adjacency list representation of graph
from collections import defaultdict
import sys
class Heap():
def __init__(self):
self.array = []
self.size = 0
self.pos = []
def newMinHeapNode(self, v, dist):
minHeapNode = [v, dist]
return minHeapNode
# A utility function to swap two nodes of
# min heap. Needed for min heapify
def swapMinHeapNode(self, a, b):
t = self.array[a]
self.array[a] = self.array[b]
self.array[b] = t
# A standard function to heapify at given idx
# This function also updates position of nodes
# when they are swapped. Position is needed
# for decreaseKey()
def minHeapify(self, idx):
smallest = idx
left = 2 * idx + 1
right = 2 * idx + 2
if left < self.size and self.array[left][1] < \
self.array[smallest][1]:
smallest = left
if right < self.size and self.array[right][1] < \
self.array[smallest][1]:
smallest = right
# The nodes to be swapped in min heap
# if idx is not smallest
if smallest != idx:
# Swap positions
self.pos[self.array[smallest][0]] = idx
self.pos[self.array[idx][0]] = smallest
# Swap nodes
self.swapMinHeapNode(smallest, idx)
self.minHeapify(smallest)
# Standard function to extract minimum node from heap
def extractMin(self):
# Return NULL wif heap is empty
if self.isEmpty() == True:
return
# Store the root node
root = self.array[0]
# Replace root node with last node
lastNode = self.array[self.size - 1]
self.array[0] = lastNode
# Update position of last node
self.pos[lastNode[0]] = 0
self.pos[root[0]] = self.size - 1
# Reduce heap size and heapify root
self.size -= 1
self.minHeapify(0)
return root
def isEmpty(self):
return True if self.size == 0 else False
def decreaseKey(self, v, dist):
# Get the index of v in heap array
i = self.pos[v]
# Get the node and update its dist value
self.array[i][1] = dist
# Travel up while the complete tree is not
# hepified. This is a O(Logn) loop
while i > 0 and self.array[i][1] < \
self.array[(i - 1) // 2][1]:
# Swap this node with its parent
self.pos[self.array[i][0]] = (i-1)/2
self.pos[self.array[(i-1)//2][0]] = i
self.swapMinHeapNode(i, (i - 1)//2)
# move to parent index
i = (i - 1) // 2
# A utility function to check if a given vertex
# 'v' is in min heap or not
def isInMinHeap(self, v):
if self.pos[v] < self.size:
return True
return False
def printArr(parent, n):
for i in range(1, n):
print("% d - % d" % (parent[i], i))
class Graph():
def __init__(self, V):
self.V = V
self.graph = defaultdict(list)
# Adds an edge to an undirected graph
def addEdge(self, src, dest, weight):
# Add an edge from src to dest. A new node is
# added to the adjacency list of src. The node
# is added at the beginning. The first element of
# the node has the destination and the second
# elements has the weight
newNode = [dest, weight]
self.graph[src].insert(0, newNode)
# Since graph is undirected, add an edge from
# dest to src also
newNode = [src, weight]
self.graph[dest].insert(0, newNode)
# The main function that prints the Minimum
# Spanning Tree(MST) using the Prim's Algorithm.
# It is a O(ELogV) function
def PrimMST(self):
# Get the number of vertices in graph
V = self.V
# key values used to pick minimum weight edge in cut
key = []
# List to store constructed MST
parent = []
# minHeap represents set E
minHeap = Heap()
# Initialize min heap with all vertices. Key values of all
# vertices (except the 0th vertex) is is initially infinite
for v in range(V):
parent.append(-1)
key.append(1e7)
minHeap.array.append(minHeap.newMinHeapNode(v, key[v]))
minHeap.pos.append(v)
# Make key value of 0th vertex as 0 so
# that it is extracted first
minHeap.pos[0] = 0
key[0] = 0
minHeap.decreaseKey(0, key[0])
# Initially size of min heap is equal to V
minHeap.size = V
# In the following loop, min heap contains all nodes
# not yet added in the MST.
while minHeap.isEmpty() == False:
# Extract the vertex with minimum distance value
newHeapNode = minHeap.extractMin()
u = newHeapNode[0]
# Traverse through all adjacent vertices of u
# (the extracted vertex) and update their
# distance values
for pCrawl in self.graph[u]:
v = pCrawl[0]
# If shortest distance to v is not finalized
# yet, and distance to v through u is less than
# its previously calculated distance
if minHeap.isInMinHeap(v) and pCrawl[1] < key[v]:
key[v] = pCrawl[1]
parent[v] = u
# update distance value in min heap also
minHeap.decreaseKey(v, key[v])
printArr(parent, V)
# Driver program to test the above functions
graph = Graph(9)
graph.addEdge(0, 1, 4)
graph.addEdge(0, 7, 8)
graph.addEdge(1, 2, 8)
graph.addEdge(1, 7, 11)
graph.addEdge(2, 3, 7)
graph.addEdge(2, 8, 2)
graph.addEdge(2, 5, 4)
graph.addEdge(3, 4, 9)
graph.addEdge(3, 5, 14)
graph.addEdge(4, 5, 10)
graph.addEdge(5, 6, 2)
graph.addEdge(6, 7, 1)
graph.addEdge(6, 8, 6)
graph.addEdge(7, 8, 7)
graph.PrimMST()
# This code is contributed by Divyanshu Mehta
Javascript
<script>
// Javascript program for Prim's MST for
// adjacency list representation of graph
class node1
{
constructor(a,b)
{
this.dest = a;
this.weight = b;
}
}
class Graph
{
constructor(e)
{
this.V=e;
this.adj = new Array(V);
for (let o = 0; o < V; o++)
this.adj[o] = [];
}
}
// class to represent a node in PriorityQueue
// Stores a vertex and its corresponding
// key value
class node
{
constructor()
{
this.vertex=0;
this.key=0;
}
}
// method to add an edge
// between two vertices
function addEdge(graph,src,dest,weight)
{
let node0 = new node1(dest, weight);
let node = new node1(src, weight);
graph.adj[src].push(node0);
graph.adj[dest].push(node);
}
// method used to find the mst
function prims_mst(graph)
{
// Whether a vertex is in PriorityQueue or not
let mstset = new Array(graph.V);
let e = new Array(graph.V);
// Stores the parents of a vertex
let parent = new Array(graph.V);
for (let o = 0; o < graph.V; o++)
{
e[o] = new node();
}
for (let o = 0; o < graph.V; o++) {
// Initialize to false
mstset[o] = false;
// Initialize key values to infinity
e[o].key = Number.MAX_VALUE;
e[o].vertex = o;
parent[o] = -1;
}
// Include the source vertex in mstset
mstset[0] = true;
// Set key value to 0
// so that it is extracted first
// out of PriorityQueue
e[0].key = 0;
// Use TreeSet instead of PriorityQueue as the remove function of the PQ is O(n) in java.
let queue = [];
for (let o = 0; o < graph.V; o++)
queue.push(e[o]);
queue.sort(function(a,b){return a.key-b.key;});
// Loops until the queue is not empty
while (queue.length!=0) {
// Extracts a node with min key value
let node0 = queue.shift();
// Include that node into mstset
mstset[node0.vertex] = true;
// For all adjacent vertex of the extracted vertex V
for (let iterator of graph.adj[node0.vertex].values()) {
// If V is in queue
if (mstset[iterator.dest] == false) {
// If the key value of the adjacent vertex is
// more than the extracted key
// update the key value of adjacent vertex
// to update first remove and add the updated vertex
if (e[iterator.dest].key > iterator.weight) {
queue.splice(queue.indexOf(e[iterator.dest]),1);
e[iterator.dest].key = iterator.weight;
queue.push(e[iterator.dest]);
queue.sort(function(a,b){return a.key-b.key;});
parent[iterator.dest] = node0.vertex;
}
}
}
}
// Prints the vertex pair of mst
for (let o = 1; o < graph.V; o++)
document.write(parent[o] + " "
+ "-"
+ " " + o+"<br>");
}
let V = 9;
let graph = new Graph(V);
addEdge(graph, 0, 1, 4);
addEdge(graph, 0, 7, 8);
addEdge(graph, 1, 2, 8);
addEdge(graph, 1, 7, 11);
addEdge(graph, 2, 3, 7);
addEdge(graph, 2, 8, 2);
addEdge(graph, 2, 5, 4);
addEdge(graph, 3, 4, 9);
addEdge(graph, 3, 5, 14);
addEdge(graph, 4, 5, 10);
addEdge(graph, 5, 6, 2);
addEdge(graph, 6, 7, 1);
addEdge(graph, 6, 8, 6);
addEdge(graph, 7, 8, 7);
// Method invoked
prims_mst(graph);
// This code is contributed by avanitrachhadiya2155
</script>
0 - 1 5 - 2 2 - 3 3 - 4 6 - 5 7 - 6 0 - 7 2 - 8
Complejidad del tiempo:
La complejidad de tiempo del código/algoritmo anterior parece O(V^2) ya que hay dos bucles while anidados. Si observamos más de cerca, podemos observar que las declaraciones en el ciclo interno se ejecutan veces O (V + E) (similar a BFS). El ciclo interno tiene una operación de disminución de clave() que toma el tiempo O (LogV). Entonces, la complejidad temporal general es O(E+V)*O(LogV) que es O((E+V)*LogV) = O(ELogV) (Para un gráfico conectado, V = O(E))
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA