Dado un árbol n-ario muy grande. Donde el Node raíz tiene alguna información que quiere pasar a todos sus hijos hasta las hojas con la restricción de que solo puede pasar la información a uno de sus hijos a la vez (tómalo como una iteración).
Ahora, en la próxima iteración, el Node hijo puede transferir esa información a solo uno de sus hijos y, al mismo tiempo, el padre del hijo, es decir, la raíz, puede pasar la información a uno de sus hijos restantes. Continuando de esta manera, tenemos que encontrar el número mínimo de iteraciones necesarias para pasar la información a todos los Nodes del árbol.
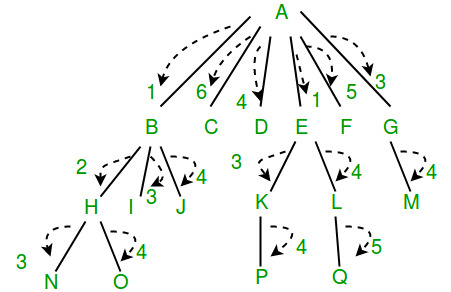
El número mínimo de iteraciones para el árbol a continuación es 6. La raíz A primero pasa información a B. En la siguiente iteración, A pasa información a E y B pasa información a H y así sucesivamente.
Recomendamos encarecidamente minimizar el navegador y probarlo usted mismo primero.
Esto se puede hacer usando Post Order Traversal. La idea es considerar la altura y los niños cuentan en todos y cada uno de los Nodes.
Si un Node secundario i toma iteraciones ci para pasar información debajo de su subárbol, entonces su padre tomará (ci + 1) iteraciones para pasar información al subárbol enraizado en ese niño i.
Si el padre tiene más hijos, les pasará información en iteraciones posteriores. Digamos que los hijos de un padre toman c1, c2, c3, c4, …, cn iteraciones para pasar información en su propio subárbol. Ahora el padre tiene que pasar información a estos n hijos uno por uno en n iteraciones. Si el padre elige al hijo i en la i-ésima iteración, entonces el padre tomará (i + ci) iteraciones para pasar información al hijo i y todo su subárbol.
En cualquier iteración, cuando el padre pasa información a un hijo i+1, los hijos (1 a i) que ya obtuvieron información del padre en iteraciones anteriores, pasarán información más abajo en iteraciones posteriores, si algún hijo (1 a i) tiene su propio hijo más abajo.
Para pasar información a todo el árbol en iteraciones mínimas, debe asegurarse de que el ancho de banda se utilice de la manera más eficiente posible (es decir, el número máximo de Nodes transitables debe pasar información más abajo en cualquier iteración)
El mejor escenario posible sería que en la iteración n, n Nodes diferentes pasen información a su hijo.
Nodes con altura = 0: (Caso trivial) El Node hoja no tiene hijos (no se necesita pasar información), por lo que ninguna de las iteraciones sería CERO.
Nodes con altura = 1: aquí el Node tiene que pasar información a todos los hijos uno por uno (todos los hijos son Nodes de hoja, por lo que no pasa más información más abajo). Dado que todos los niños son hoja, el Node puede pasar información a cualquier niño en cualquier orden (elija a cualquier niño que aún no haya recibido la información). Se necesita una iteración para cada hijo, por lo que ninguna de las iteraciones sería ninguna de los hijos. Entonces, el Node con altura 1 con n hijos tomará n iteraciones.
Tome un contador inicializado con CERO, recorra todos los elementos secundarios y siga incrementando el contador.
Nodes con altura > 1: supongamos que hay n hijos (1 a n) de un Node y que las iteraciones mínimas para todos los n hijos son c1, c2, …., cn.
Para asegurarse de que el número máximo de Nodes participe en el paso de información en cualquier iteración, el padre primero debe pasar información a ese hijo que tomará la iteración máxima para pasar información más abajo en iteraciones posteriores. es decir, en cualquier iteración, el padre debe elegir al hijo que realiza la máxima iteración más adelante. Se puede considerar como un enfoque codicioso en el que los padres eligen primero al niño, que necesita el máximo número de iteraciones para que todas las iteraciones posteriores se puedan utilizar de manera eficiente.
Si el padre va de otra manera, entonces, al final, podría haber algunos Nodes que se realizan bastante temprano, permaneciendo inactivos y, por lo tanto, el ancho de banda no se utiliza de manera eficiente en iteraciones posteriores.
Si hay dos hijos i y j con iteraciones mínimas ci y cj donde ci > cj, entonces si el padre elige al hijo j primero, entonces ninguna de las iteraciones que necesita el padre para pasar información a ambos hijos y su subárbol sería: max (1 + cj , 2 + ci) = 2 + ci
Si el padre elige al hijo i primero, entonces ninguna de las iteraciones que necesita el padre para pasar información a ambos hijos y su subárbol sería: max (1 + ci, 2 + cj) = 1 + ci (Por lo tanto, elegir ci da un mejor resultado que elegir cj)
Esto dice que el padre siempre debe elegir el hijo i con el valor máximo de ci en cualquier iteración.
SO aquí el enfoque codicioso es:
ordenar todos los valores ci en orden decreciente,
digamos después de ordenar, los valores son c1 > c2 > c3 > …. > cn
tome un contador c, establezca c = 1 + c1 (para el niño con el número máximo de iteraciones)
para todos los niños i de 2 a n, c = c + 1 + ci
, entonces el número total de iteraciones que necesita el padre es max(n , C)
Sea minItr(A) la iteración mínima necesaria para pasar información del Node A a todo el subárbol. Sea child(A) el conteo de todos los hijos del Node A. Entonces, la relación recursiva sería:
1. Get minItr(B) of all children (B) of a node (A)
2. Sort all minItr(B) in descending order
3. Get minItr of A based on all minItr(B)
minItr(A) = child(A)
For children B from i = 0 to child(A)
minItr(A) = max ( minItr(A), minItr(B) + i + 1)
Base cases would be:
If node is leaf, minItr = 0
If node's height is 1, minItr = children count
A continuación se muestra la implementación de la idea anterior.
C++
// C++ program to find minimum number of iterations to pass
// information from root to all nodes in an n-ary tree
#include<bits/stdc++.h>
using namespace std;
// A class to represent n-ary tree (Note that the implementation
// is similar to graph for simplicity of implementation
class NAryTree
{
int N; // No. of nodes in Tree
// Pointer to an array containing list of children
list<int> *adj;
// A function used by getMinIter(), it basically does postorder
void getMinIterUtil(int v, int minItr[]);
public:
NAryTree(int N); // Constructor
// function to add a child w to v
void addChild(int v, int w);
// The main function to find minimum iterations
int getMinIter();
static int compare(const void * a, const void * b);
};
NAryTree::NAryTree(int N)
{
this->N = N;
adj = new list<int>[N];
}
// To add a child w to v
void NAryTree::addChild(int v, int w)
{
adj[v].push_back(w); // Add w to v’s list.
}
/* A recursive function to used by getMinIter(). This function
// mainly does postorder traversal and get minimum iteration of all children
// of node u, sort them in decreasing order and then get minimum iteration
// of node u
1. Get minItr(B) of all children (B) of a node (A)
2. Sort all minItr(B) in descending order
3. Get minItr of A based on all minItr(B)
minItr(A) = child(A) -->> child(A) is children count of node A
For children B from i = 0 to child(A)
minItr(A) = max ( minItr(A), minItr(B) + i + 1)
Base cases would be:
If node is leaf, minItr = 0
If node's height is 1, minItr = children count
*/
void NAryTree::getMinIterUtil(int u, int minItr[])
{
minItr[u] = adj[u].size();
int *minItrTemp = new int[minItr[u]];
int k = 0, tmp = 0;
// Recur for all the vertices adjacent to this vertex
list<int>::iterator i;
for (i = adj[u].begin(); i!= adj[u].end(); ++i)
{
getMinIterUtil(*i, minItr);
minItrTemp[k++] = minItr[*i];
}
qsort(minItrTemp, minItr[u], sizeof (int), compare);
for (k = 0; k < adj[u].size(); k++)
{
tmp = minItrTemp[k] + k + 1;
minItr[u] = max(minItr[u], tmp);
}
delete[] minItrTemp;
}
// The function to do PostOrder traversal. It uses
// recursive getMinIterUtil()
int NAryTree::getMinIter()
{
// Set minimum iteration all the vertices as zero
int *minItr = new int[N];
int res = -1;
for (int i = 0; i < N; i++)
minItr[i] = 0;
// Start Post Order Traversal from Root
getMinIterUtil(0, minItr);
res = minItr[0];
delete[] minItr;
return res;
}
int NAryTree::compare(const void * a, const void * b)
{
return ( *(int*)b - *(int*)a );
}
// Driver function to test above functions
int main()
{
// TestCase 1
NAryTree tree1(17);
tree1.addChild(0, 1);
tree1.addChild(0, 2);
tree1.addChild(0, 3);
tree1.addChild(0, 4);
tree1.addChild(0, 5);
tree1.addChild(0, 6);
tree1.addChild(1, 7);
tree1.addChild(1, 8);
tree1.addChild(1, 9);
tree1.addChild(4, 10);
tree1.addChild(4, 11);
tree1.addChild(6, 12);
tree1.addChild(7, 13);
tree1.addChild(7, 14);
tree1.addChild(10, 15);
tree1.addChild(11, 16);
cout << "TestCase 1 - Minimum Iteration: "
<< tree1.getMinIter() << endl;
// TestCase 2
NAryTree tree2(3);
tree2.addChild(0, 1);
tree2.addChild(0, 2);
cout << "TestCase 2 - Minimum Iteration: "
<< tree2.getMinIter() << endl;
// TestCase 3
NAryTree tree3(1);
cout << "TestCase 3 - Minimum Iteration: "
<< tree3.getMinIter() << endl;
// TestCase 4
NAryTree tree4(6);
tree4.addChild(0, 1);
tree4.addChild(1, 2);
tree4.addChild(2, 3);
tree4.addChild(3, 4);
tree4.addChild(4, 5);
cout << "TestCase 4 - Minimum Iteration: "
<< tree4.getMinIter() << endl;
// TestCase 5
NAryTree tree5(6);
tree5.addChild(0, 1);
tree5.addChild(0, 2);
tree5.addChild(2, 3);
tree5.addChild(2, 4);
tree5.addChild(2, 5);
cout << "TestCase 5 - Minimum Iteration: "
<< tree5.getMinIter() << endl;
// TestCase 6
NAryTree tree6(6);
tree6.addChild(0, 1);
tree6.addChild(0, 2);
tree6.addChild(2, 3);
tree6.addChild(2, 4);
tree6.addChild(3, 5);
cout << "TestCase 6 - Minimum Iteration: "
<< tree6.getMinIter() << endl;
// TestCase 7
NAryTree tree7(14);
tree7.addChild(0, 1);
tree7.addChild(0, 2);
tree7.addChild(0, 3);
tree7.addChild(1, 4);
tree7.addChild(2, 5);
tree7.addChild(2, 6);
tree7.addChild(4, 7);
tree7.addChild(5, 8);
tree7.addChild(5, 9);
tree7.addChild(7, 10);
tree7.addChild(8, 11);
tree7.addChild(8, 12);
tree7.addChild(10, 13);
cout << "TestCase 7 - Minimum Iteration: "
<< tree7.getMinIter() << endl;
// TestCase 8
NAryTree tree8(14);
tree8.addChild(0, 1);
tree8.addChild(0, 2);
tree8.addChild(0, 3);
tree8.addChild(0, 4);
tree8.addChild(0, 5);
tree8.addChild(1, 6);
tree8.addChild(2, 7);
tree8.addChild(3, 8);
tree8.addChild(4, 9);
tree8.addChild(6, 10);
tree8.addChild(7, 11);
tree8.addChild(8, 12);
tree8.addChild(9, 13);
cout << "TestCase 8 - Minimum Iteration: "
<< tree8.getMinIter() << endl;
// TestCase 9
NAryTree tree9(25);
tree9.addChild(0, 1);
tree9.addChild(0, 2);
tree9.addChild(0, 3);
tree9.addChild(0, 4);
tree9.addChild(0, 5);
tree9.addChild(0, 6);
tree9.addChild(1, 7);
tree9.addChild(2, 8);
tree9.addChild(3, 9);
tree9.addChild(4, 10);
tree9.addChild(5, 11);
tree9.addChild(6, 12);
tree9.addChild(7, 13);
tree9.addChild(8, 14);
tree9.addChild(9, 15);
tree9.addChild(10, 16);
tree9.addChild(11, 17);
tree9.addChild(12, 18);
tree9.addChild(13, 19);
tree9.addChild(14, 20);
tree9.addChild(15, 21);
tree9.addChild(16, 22);
tree9.addChild(17, 23);
tree9.addChild(19, 24);
cout << "TestCase 9 - Minimum Iteration: "
<< tree9.getMinIter() << endl;
return 0;
}
Java
// Java program to find minimum number of
// iterations to pass information from
// root to all nodes in an n-ary tree
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.Iterator;
import java.util.List;
class GFG
{
// No. of nodes
private static int N;
// Adjacency list containing
// list of children
private static List<List<Integer>> adj;
GFG(int N)
{
this.N = N;
adj = new ArrayList<>(N);
for (int i = 0; i < N; i++)
adj.add(new ArrayList<>());
}
// function to add a child w to v
void addChild(int v, int w)
{
adj.get(v).add(w);
}
// Main function to find the
// minimum iterations
private int getMinIteration()
{
// Base case : if height = 0 or 1;
if (N == 0 || N == 1)
return 0;
int[] mintItr = new int[N];
// Start Post Order Traversal from Root
getMinIterUtil(0, mintItr);
return mintItr[0];
}
/* A recursive function to used by getMinIter().
This function mainly does postorder traversal
and get minimum iteration of all children
of parent node, sort them in decreasing order
and then get minimum iteration of parent node
1. Get minItr(B) of all children (B) of a node (A)
2. Sort all minItr(B) in descending order
3. Get minItr of A based on all minItr(B)
minItr(A) = child(A) -->> child(A)
is children count of node A
For children B from i = 0 to child(A)
minItr(A) = max (minItr(A),
minItr(B) + i + 1)
Base cases would be:
If node is leaf, minItr = 0
If node's height is 1, minItr = children count
*/
private void getMinIterUtil(int u, int[] minItr)
{
// Base case : Leaf node
if (adj.get(u).size() == 0)
return;
minItr[u] = adj.get(u).size();
Integer[] minItrTemp = new Integer[minItr[u]];
int k = 0;
Iterator itr = adj.get(u).iterator();
while (itr.hasNext())
{
int currentChild = (int) itr.next();
getMinIterUtil(currentChild, minItr);
minItrTemp[k++] = minItr[currentChild];
}
Arrays.sort(minItrTemp, Collections.reverseOrder());
for (k = 0; k < adj.get(u).size(); k++)
{
int temp = minItrTemp[k] + k + 1;
minItr[u] = Math.max(minItr[u], temp);
}
}
// Driver Code
public static void main(String args[])
{
// TestCase1
GFG testCase1 = new GFG(17);
testCase1.addChild(0, 1);
testCase1.addChild(0, 2);
testCase1.addChild(0, 3);
testCase1.addChild(0, 4);
testCase1.addChild(0, 5);
testCase1.addChild(0, 6);
testCase1.addChild(1, 7);
testCase1.addChild(1, 8);
testCase1.addChild(1, 9);
testCase1.addChild(4, 10);
testCase1.addChild(4, 11);
testCase1.addChild(6, 12);
testCase1.addChild(7, 13);
testCase1.addChild(7, 14);
testCase1.addChild(10, 15);
testCase1.addChild(11, 16);
System.out.println("TestCase 1 - Minimum Iteration: " +
testCase1.getMinIteration());
// TestCase2
GFG testCase2 = new GFG(3);
testCase2.addChild(0, 1);
testCase2.addChild(0, 2);
System.out.println("TestCase 2 - Minimum Iteration: " +
testCase2.getMinIteration());
// TestCase3
GFG testCase3 = new GFG(1);
System.out.println("TestCase 3 - Minimum Iteration: " +
testCase3.getMinIteration());
// TestCase4
GFG testCase4 = new GFG(6);
testCase4.addChild(0, 1);
testCase4.addChild(1, 2);
testCase4.addChild(2, 3);
testCase4.addChild(3, 4);
testCase4.addChild(4, 5);
System.out.println("TestCase 4 - Minimum Iteration: " +
testCase4.getMinIteration());
// TestCase 5
GFG testCase5 = new GFG(6);
testCase5.addChild(0, 1);
testCase5.addChild(0, 2);
testCase5.addChild(2, 3);
testCase5.addChild(2, 4);
testCase5.addChild(2, 5);
System.out.println("TestCase 5 - Minimum Iteration: " +
testCase5.getMinIteration());
// TestCase 6
GFG testCase6 = new GFG(6);
testCase6.addChild(0, 1);
testCase6.addChild(0, 2);
testCase6.addChild(2, 3);
testCase6.addChild(2, 4);
testCase6.addChild(3, 5);
System.out.println("TestCase 6 - Minimum Iteration: " +
testCase6.getMinIteration());
// TestCase 7
GFG testCase7 = new GFG(14);
testCase7.addChild(0, 1);
testCase7.addChild(0, 2);
testCase7.addChild(0, 3);
testCase7.addChild(1, 4);
testCase7.addChild(2, 5);
testCase7.addChild(2, 6);
testCase7.addChild(4, 7);
testCase7.addChild(5, 8);
testCase7.addChild(5, 9);
testCase7.addChild(7, 10);
testCase7.addChild(8, 11);
testCase7.addChild(8, 12);
testCase7.addChild(10, 13);
System.out.println("TestCase 7 - Minimum Iteration: " +
testCase7.getMinIteration());
// TestCase 8
GFG testCase8 = new GFG(14);
testCase8.addChild(0, 1);
testCase8.addChild(0, 2);
testCase8.addChild(0, 3);
testCase8.addChild(0, 4);
testCase8.addChild(0, 5);
testCase8.addChild(1, 6);
testCase8.addChild(2, 7);
testCase8.addChild(3, 8);
testCase8.addChild(4, 9);
testCase8.addChild(6, 10);
testCase8.addChild(7, 11);
testCase8.addChild(8, 12);
testCase8.addChild(9, 13);
System.out.println("TestCase 8 - Minimum Iteration: " +
testCase8.getMinIteration());
// TestCase 9
GFG testCase9 = new GFG(25);
testCase9.addChild(0, 1);
testCase9.addChild(0, 2);
testCase9.addChild(0, 3);
testCase9.addChild(0, 4);
testCase9.addChild(0, 5);
testCase9.addChild(0, 6);
testCase9.addChild(1, 7);
testCase9.addChild(2, 8);
testCase9.addChild(3, 9);
testCase9.addChild(4, 10);
testCase9.addChild(5, 11);
testCase9.addChild(6, 12);
testCase9.addChild(7, 13);
testCase9.addChild(8, 14);
testCase9.addChild(9, 15);
testCase9.addChild(10, 16);
testCase9.addChild(11, 17);
testCase9.addChild(12, 18);
testCase9.addChild(13, 19);
testCase9.addChild(14, 20);
testCase9.addChild(15, 21);
testCase9.addChild(16, 22);
testCase9.addChild(17, 23);
testCase9.addChild(19, 24);
System.out.println("TestCase 9 - Minimum Iteration: " +
testCase9.getMinIteration());
}
}
// This code is contributed
// by MitaliSrivastava
C#
// C# program to find minimum number of
// iterations to pass information from
// root to all nodes in an n-ary tree
using System;
using System.Collections.Generic;
class GFG
{
// No. of nodes
public int N;
// Adjacency list containing
// list of children
static List<List<int>> adj;
public GFG(int N)
{
this.N = N;
adj = new List<List<int>>(N);
for (int i = 0; i < N; i++)
adj.Add(new List<int>());
}
// function to add a child w to v
void addChild(int v, int w)
{
adj[v].Add(w);
}
// Main function to find the
// minimum iterations
private int getMinIteration()
{
// Base case : if height = 0 or 1;
if (N == 0 || N == 1)
return 0;
int[] mintItr = new int[N];
// Start Post Order Traversal from Root
getMinIterUtil(0, mintItr);
return mintItr[0];
}
/* A recursive function to used by getMinIter().
This function mainly does postorder traversal
and get minimum iteration of all children
of parent node, sort them in decreasing order
and then get minimum iteration of parent node
1. Get minItr(B) of all children (B) of a node (A)
2. Sort all minItr(B) in descending order
3. Get minItr of A based on all minItr(B)
minItr(A) = child(A) -->> child(A)
is children count of node A
For children B from i = 0 to child(A)
minItr(A) = max (minItr(A),
minItr(B) + i + 1)
Base cases would be:
If node is leaf, minItr = 0
If node's height is 1, minItr = children count
*/
private void getMinIterUtil(int u, int[] minItr)
{
// Base case : Leaf node
if (adj[u].Count == 0)
return;
minItr[u] = adj[u].Count;
int[] minItrTemp = new int[minItr[u]];
int k = 0;
// Iterator itr = adj.get(u).iterator();
foreach (int itr in adj[u])
{
int currentChild = (int) itr;
getMinIterUtil(currentChild, minItr);
minItrTemp[k++] = minItr[currentChild];
}
Array.Sort(minItrTemp);
for(int i =0, j = minItrTemp.Length-1; i<j;i++,j--){
int temp = minItrTemp[i];
minItrTemp[i] = minItrTemp[j];
minItrTemp[j] = temp;
}
for (k = 0; k < adj[u].Count; k++)
{
int temp = minItrTemp[k] + k + 1;
minItr[u] = Math.Max(minItr[u], temp);
}
}
// Driver Code
public static void Main(String []args)
{
// TestCase1
GFG testCase1 = new GFG(17);
testCase1.addChild(0, 1);
testCase1.addChild(0, 2);
testCase1.addChild(0, 3);
testCase1.addChild(0, 4);
testCase1.addChild(0, 5);
testCase1.addChild(0, 6);
testCase1.addChild(1, 7);
testCase1.addChild(1, 8);
testCase1.addChild(1, 9);
testCase1.addChild(4, 10);
testCase1.addChild(4, 11);
testCase1.addChild(6, 12);
testCase1.addChild(7, 13);
testCase1.addChild(7, 14);
testCase1.addChild(10, 15);
testCase1.addChild(11, 16);
Console.WriteLine("TestCase 1 - Minimum Iteration: " +
testCase1.getMinIteration());
// TestCase2
GFG testCase2 = new GFG(3);
testCase2.addChild(0, 1);
testCase2.addChild(0, 2);
Console.WriteLine("TestCase 2 - Minimum Iteration: " +
testCase2.getMinIteration());
// TestCase3
GFG testCase3 = new GFG(1);
Console.WriteLine("TestCase 3 - Minimum Iteration: " +
testCase3.getMinIteration());
// TestCase4
GFG testCase4 = new GFG(6);
testCase4.addChild(0, 1);
testCase4.addChild(1, 2);
testCase4.addChild(2, 3);
testCase4.addChild(3, 4);
testCase4.addChild(4, 5);
Console.WriteLine("TestCase 4 - Minimum Iteration: " +
testCase4.getMinIteration());
// TestCase 5
GFG testCase5 = new GFG(6);
testCase5.addChild(0, 1);
testCase5.addChild(0, 2);
testCase5.addChild(2, 3);
testCase5.addChild(2, 4);
testCase5.addChild(2, 5);
Console.WriteLine("TestCase 5 - Minimum Iteration: " +
testCase5.getMinIteration());
// TestCase 6
GFG testCase6 = new GFG(6);
testCase6.addChild(0, 1);
testCase6.addChild(0, 2);
testCase6.addChild(2, 3);
testCase6.addChild(2, 4);
testCase6.addChild(3, 5);
Console.WriteLine("TestCase 6 - Minimum Iteration: " +
testCase6.getMinIteration());
// TestCase 7
GFG testCase7 = new GFG(14);
testCase7.addChild(0, 1);
testCase7.addChild(0, 2);
testCase7.addChild(0, 3);
testCase7.addChild(1, 4);
testCase7.addChild(2, 5);
testCase7.addChild(2, 6);
testCase7.addChild(4, 7);
testCase7.addChild(5, 8);
testCase7.addChild(5, 9);
testCase7.addChild(7, 10);
testCase7.addChild(8, 11);
testCase7.addChild(8, 12);
testCase7.addChild(10, 13);
Console.WriteLine("TestCase 7 - Minimum Iteration: " +
testCase7.getMinIteration());
// TestCase 8
GFG testCase8 = new GFG(14);
testCase8.addChild(0, 1);
testCase8.addChild(0, 2);
testCase8.addChild(0, 3);
testCase8.addChild(0, 4);
testCase8.addChild(0, 5);
testCase8.addChild(1, 6);
testCase8.addChild(2, 7);
testCase8.addChild(3, 8);
testCase8.addChild(4, 9);
testCase8.addChild(6, 10);
testCase8.addChild(7, 11);
testCase8.addChild(8, 12);
testCase8.addChild(9, 13);
Console.WriteLine("TestCase 8 - Minimum Iteration: " +
testCase8.getMinIteration());
// TestCase 9
GFG testCase9 = new GFG(25);
testCase9.addChild(0, 1);
testCase9.addChild(0, 2);
testCase9.addChild(0, 3);
testCase9.addChild(0, 4);
testCase9.addChild(0, 5);
testCase9.addChild(0, 6);
testCase9.addChild(1, 7);
testCase9.addChild(2, 8);
testCase9.addChild(3, 9);
testCase9.addChild(4, 10);
testCase9.addChild(5, 11);
testCase9.addChild(6, 12);
testCase9.addChild(7, 13);
testCase9.addChild(8, 14);
testCase9.addChild(9, 15);
testCase9.addChild(10, 16);
testCase9.addChild(11, 17);
testCase9.addChild(12, 18);
testCase9.addChild(13, 19);
testCase9.addChild(14, 20);
testCase9.addChild(15, 21);
testCase9.addChild(16, 22);
testCase9.addChild(17, 23);
testCase9.addChild(19, 24);
Console.WriteLine("TestCase 9 - Minimum Iteration: " +
testCase9.getMinIteration());
}
}
// This code is contributed by aashish1995
Javascript
<script>
var height;
var graph;
function findHeight(node , h)
{
height[node] = h;
for(let i=0;i<graph[node].length;i++)
{
let v = graph[node][i];
findHeight(v , h + 1);
}
}
function getMinIteration()
{
findHeight(0 , 0);
let max_height = 0;
for(let i=0;i<height.length;i++)
{
if(height[i] > max_height)
{
max_height = height[i];
}
}
for(let i=0;i<height.length;i++)
{
height[i] = max_height - height[i];
}
return getMinIterationUtil(0);
}
function getMinIterationUtil(node)
{
if(height[node] == 0 )
{
return 0;
}
if(height[node] == 1 )
{
return graph[node].length;
}
let edges =[...graph[node] ];
let edgeLenArr = [];
for(let i=0;i<edges.length;i++ )
{
edgeLenArr.push( graph[ graph[node][i] ].length );
}
for (let i = 0; i < edgeLenArr.length - 1; i++) {
for (let j = i + 1; j < edgeLenArr.length; j++) {
if(edgeLenArr[i] < edgeLenArr[j])
{
let temp = edgeLenArr[i];
edgeLenArr[i] = edgeLenArr[j];
edgeLenArr[j] = temp;
let temp1 = edges[i];
edges[i] = edges[j];
edges[j] = temp1;
}
}
}
let max_data = edges.length;
for(let i=0;i<edges.length;i++)
{
max_data = Math.max( max_data , i + 1 + getMinIterationUtil(edges[i]));
}
return max_data;
}
function addChild(a , b)
{
graph[a].push(b);
}
function intializeGraph(n)
{
height = new Array(n);
height.fill(0);
graph = new Array(n);
for(let i=0;i<graph.length;i++)
{ graph[i] = []; }
}
// TestCase1
intializeGraph(17);
addChild(0, 1);
addChild(0, 2);
addChild(0, 3);
addChild(0, 4);
addChild(0, 5);
addChild(0, 6);
addChild(1, 7);
addChild(1, 8);
addChild(1, 9);
addChild(4, 10);
addChild(4, 11);
addChild(6, 12);
addChild(7, 13);
addChild(7, 14);
addChild(10, 15);
addChild(11, 16);
document.write("TestCase 1 - Minimum Iteration: " + getMinIteration());
document.write('<br>');
document.write('<br>');
// TestCase2
intializeGraph(3);
addChild(0, 1);
addChild(0, 2);
document.write("TestCase 2 - Minimum Iteration: " + getMinIteration());
document.write('<br>');
document.write('<br>');
// TestCase3
intializeGraph(1);
document.write("TestCase 3 - Minimum Iteration: " + getMinIteration(1));
document.write('<br>');
document.write('<br>');
// // TestCase4
intializeGraph(6);
addChild(0, 1);
addChild(1, 2);
addChild(2, 3);
addChild(3, 4);
addChild(4, 5);
document.write("TestCase 4 - Minimum Iteration: " + getMinIteration());
document.write('<br>');
document.write('<br>');
// TestCase 5
intializeGraph(6);
addChild(0, 1);
addChild(0, 2);
addChild(2, 3);
addChild(2, 4);
addChild(2, 5);
document.write("TestCase 5 - Minimum Iteration: " + getMinIteration());
document.write('<br>');
document.write('<br>');
// TestCase 6
intializeGraph(6);
addChild(0, 1);
addChild(0, 2);
addChild(2, 3);
addChild(2, 4);
addChild(3, 5);
document.write("TestCase 6 - Minimum Iteration: " + getMinIteration());
document.write('<br>');
document.write('<br>');
// TestCase 7
intializeGraph(14);
addChild(0, 1);
addChild(0, 2);
addChild(0, 3);
addChild(1, 4);
addChild(2, 5);
addChild(2, 6);
addChild(4, 7);
addChild(5, 8);
addChild(5, 9);
addChild(7, 10);
addChild(8, 11);
addChild(8, 12);
addChild(10, 13);
document.write("TestCase 7 - Minimum Iteration: " + getMinIteration());
document.write('<br>');
document.write('<br>');
// TestCase 8
intializeGraph(14);
addChild(0, 1);
addChild(0, 2);
addChild(0, 3);
addChild(0, 4);
addChild(0, 5);
addChild(1, 6);
addChild(2, 7);
addChild(3, 8);
addChild(4, 9);
addChild(6, 10);
addChild(7, 11);
addChild(8, 12);
addChild(9, 13);
document.write("TestCase 8 - Minimum Iteration: " + getMinIteration());
document.write('<br>');
document.write('<br>');
// TestCase 9
intializeGraph(25);
addChild(0, 1);
addChild(0, 2);
addChild(0, 3);
addChild(0, 4);
addChild(0, 5);
addChild(0, 6);
addChild(1, 7);
addChild(2, 8);
addChild(3, 9);
addChild(4, 10);
addChild(5, 11);
addChild(6, 12);
addChild(7, 13);
addChild(8, 14);
addChild(9, 15);
addChild(10, 16);
addChild(11, 17);
addChild(12, 18);
addChild(13, 19);
addChild(14, 20);
addChild(15, 21);
addChild(16, 22);
addChild(17, 23);
addChild(19, 24);
document.write("TestCase 9 - Minimum Iteration: " + getMinIteration(25));
document.write('<br>');
document.write('<br>');
//this code is contributed by gaurav2146
</script>
TestCase 1 - Minimum Iteration: 6 TestCase 2 - Minimum Iteration: 2 TestCase 3 - Minimum Iteration: 0 TestCase 4 - Minimum Iteration: 5 TestCase 5 - Minimum Iteration: 4 TestCase 6 - Minimum Iteration: 3 TestCase 7 - Minimum Iteration: 6 TestCase 8 - Minimum Iteration: 6 TestCase 9 - Minimum Iteration: 8
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA