Ver notas de última hora sobre todos los temas aquí .
Arrays
Una array representa una colección de números dispuestos en un orden de filas y columnas. Es necesario encerrar los elementos de una array entre paréntesis o corchetes.
A continuación se muestra una array con 9 elementos.
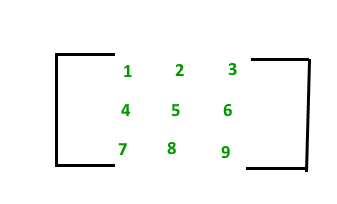
Esta Array [M] tiene 3 filas y 3 columnas. Se puede hacer referencia a cada elemento de la array [M] por su número de fila y columna. Por ejemplo, un 23 = 6
Orden de una array:
el orden de una array se define en términos de su número de filas y columnas.
Orden de una array = No. de filas × No. de columnas
Por lo tanto Matrix [M] es una array de orden 3 × 3.
Transpuesta de una array:
La transpuesta [M] T de una array mxn [M] es la array nxm obtenida al intercambiar las filas y columnas de [M].
si A= [a ij ] mxn , entonces A T = [b ij ] nxm donde b ij = a ji
Propiedades de transpuesta de una array:
- (UN T ) T = UN
- (A+B) T = UN T + B T
- (AB) T = B T UN T
Array singular y no singular:
- Array singular: se dice que una array cuadrada es array singular si su determinante es cero, es decir, |A|=0
- Array no singular: Se dice que una array cuadrada es array no singular si su determinante es distinto de cero.
Array cuadrada: una array cuadrada tiene tantas filas como columnas. es decir, número de filas = número de columnas.
Array simétrica: se dice que una array cuadrada es simétrica si la transpuesta de la array original es igual a su array original. es decir, (A T ) = A.
Sesgada simétrica: Una array sesgada simétrica (o antisimétrica o antimétrica[1]) es una array cuadrada cuya transpuesta es igual a su negativo. Es decir, (A T ) = -A.
Array diagonal: una array diagonal es una array en la que las entradas fuera de la diagonal principal son todas cero. El término generalmente se refiere a arrays cuadradas.
Array de identidad:Una array cuadrada en la que todos los elementos de la diagonal principal son unos y todos los demás elementos son ceros. La array de identidad se denota como I.
Array ortogonal: Se dice que una array es ortogonal si AA T = A T A = I
Array independiente: Se dice que una array es idemponente si A 2 = A
Array Involutaria: Se dice que una array es Involutaria si A 2 = I.
Conjunta de una array cuadrada:

Propiedades del Adjunto:
- A(Adj A) = (Adj A) A = |A| yo norte
- Adj(AB) = (Adj B).(Adj A)
- |Adj A|= |A| n-1
- Adj(kA) = k n-1 Adj(A)
Inversa de una array cuadrada:
![]()
Aquí |A| no debe ser igual a cero, significa que la array A no debe ser singular.
Propiedades de la inversa:
1. (A -1 ) -1 = A
2. (AB) -1 = B -1 A -1
3. Solo una array cuadrada no singular puede tener una inversa.
Traza de una array:
Sea A=[a ij ] nxn una array cuadrada de orden n, entonces la suma de los elementos de la diagonal se llama la traza de una array que se denota por tr(A). tr(A) = un 11 + un 22 + un 33 + ……….+ un nn . Recuerde que la traza de una array también es igual a la suma del valor propio de la array. Por ejemplo:

Propiedades de la traza de array:
Sean A y B cualesquiera dos arrays cuadradas de orden n, entonces
- tr(kA) = k tr(A) donde k es un escalar.
- tr(A+B) = tr(A)+tr(B)
- tr(AB) = tr(A)-tr(B)
- tr(AB) = tr(BA)
Solución de un sistema de ecuaciones lineales:
Las ecuaciones lineales pueden tener tres tipos de posibles soluciones:
- Sin solución
- Solución única
- Solución Infinita
Rango de una array: El rango de la array es el número de filas distintas de cero en la forma reducida de filas o el número máximo de filas independientes o el número máximo de columnas independientes.
Sea A cualquier array mxn y tiene subarrays cuadradas de diferente orden. Se dice que una array es de rango r, si cumple las siguientes propiedades:
- Tiene al menos una subarrays cuadradas de orden r que tiene determinante distinto de cero.
- Todos los determinantes de subarrays cuadradas de orden (r+1) o mayor que r son cero.
El rango se denota como P(A).
si A es una array no singular de orden n, entonces el rango de A = n, es decir, P(A) = n.
Propiedades de rango de una array:
- Si A es una array nula, entonces P(A) = 0, es decir, el rango de la array nula es cero.
- Si I n es la array unitaria nxn entonces P(A) = n.
- Rango de una array A mxn , P(A) ≤ min(m,n). Así P(A) ≤m y P(A) ≤ n.
- P(A nxn ) = n si |A| ≠ 0
- Si P(A) = m y P(B)=n entonces P(AB) ≤ min(m,n).
- Si A y B son arrays cuadradas de orden n, entonces P(AB) ? P(A) + P(B) – norte.
- Si A m×1 es una array de columna distinta de cero y B 1×n es una array de fila distinta de cero, entonces P(AB) = 1.
- El rango de una array simétrica oblicua no puede ser igual a uno.
Sistema de ecuaciones lineales homogéneas AX = 0 .
- X = 0. es siempre una solución; significa que todas las incógnitas tienen el mismo valor que cero. (Esto también se llama solución trivial)
- Si P(A) = número de incógnitas, solución única.
- Si P(A) < número de incógnitas, infinito número de soluciones.
Sistema de ecuaciones lineales no homogéneas AX = B .
- Si P[A:B] ≠P(A), Sin solución.
- Si P[A:B] = P(A) = el número de variables desconocidas, solución única.
- Si P[A:B] = P(A) ≠ número de incógnitas, número infinito de soluciones.
Aquí P[A:B] es el rango de la representación de eliminación de Gauss de AX = B.
Hay dos estados del sistema de ecuaciones lineales:
- Estado consistente: un sistema de ecuaciones que tiene una o más soluciones se denomina sistema de ecuaciones consistente.
- Estado inconsistente: un sistema de ecuaciones que no tiene soluciones se llama sistema de ecuaciones inconsistente.
Dependencia lineal e Independencia lineal del vector:
Dependencia lineal: Se dice que un conjunto de vectores X 1 ,X 2 ….X r es linealmente dependiente si existen r escalares k 1 ,k 2 …..k r tales que: k 1 X 1 + k 2 X 2 + ……..k r X r = 0.
Independencia lineal: Se dice que un conjunto de vectores X 1 ,X 2 ….X r es linealmente independiente si para todos los r escalares k 1 ,k 2 …..k r tal que k 1 X 1 + k 2 X 2 +… …..k r X r = 0, entonces k 1 = k 2 =……. = k r = 0.
¿Cómo determinar la dependencia e independencia lineal?
Sean X 1 , X 2 ….X r los vectores dados. Construya una array con los vectores dados como sus filas.
- Si el rango de la array de los vectores dados es menor que el número de vectores, entonces los vectores son linealmente dependientes.
- Si el rango de la array de los vectores dados es igual al número de vectores, entonces los vectores son linealmente independientes.
Valor propio y vector propio
El vector propio de una array A es un vector representado por una array X tal que cuando X se multiplica por la array A, la dirección de la array resultante sigue siendo la misma que la del vector X.
Matemáticamente, la declaración anterior se puede representar como:
AX = λX
donde A es cualquier array arbitraria, λ son valores propios y X es un vector propio correspondiente a cada valor propio.
Aquí podemos ver que AX es paralelo a X. Entonces, X es un vector propio.
Método para encontrar vectores propios y valores propios de cualquier array cuadrada A
Sabemos que,
AX = λX
=> AX – λX = 0
=> (A – λI) X = 0 …..(1)
La condición anterior será verdadera solo si (A – λI) es singular. Eso significa,
|A – λI| = 0 …..(2)
(2) se conoce como ecuación característica de la array.
Las raíces de la ecuación característica son los valores propios de la array A.
Ahora, para encontrar los vectores propios, simplemente colocamos cada valor propio en (1) y lo resolvemos por eliminación gaussiana, es decir, convertimos la array aumentada (A – λI) = 0 en forma escalonada por filas y resolvemos el sistema lineal de ecuaciones así obtenido.
Algunas propiedades importantes de los valores propios
- Los valores propios de arrays reales simétricas y hermíticas son reales
- Los valores propios de las arrays hermíticas sesgadas y simétricas sesgadas reales son imaginarias puras o cero
- Los valores propios de arrays unitarias y ortogonales son de módulo unitario |λ| = 1
- Si λ 1, =λ 2 …….λ n son los valores propios de A, entonces kλ 1 , kλ 2 …….kλ n son los valores propios de kA
- Si λ 1, λ 2 …….λ n son los valores propios de A, entonces 1/λ 1 , 1/λ 2 …….1/λ n son los valores propios de A -1
- Si λ 1, λ 2 …….λ n son los valores propios de A, entonces λ 1 k , λ 2 k …….λ n k son los valores propios de A k
- Valores propios de A = Valores propios de A T (transposición)
- Suma de valores propios = Traza de A (Suma de elementos diagonales de A)
- Producto de valores propios = |A|
- Número máximo de valores propios distintos de A = Tamaño de A
- Si A y B son dos arrays del mismo orden, los valores propios de AB = valores propios de BA
Probabilidad
La probabilidad se refiere al grado de ocurrencia de los eventos. Cuando ocurre un evento como lanzar una pelota, sacar una carta del mazo, etc., entonces debe haber alguna probabilidad asociada con ese evento.
Terminologías básicas:
- Evento aleatorio: si la repetición de un experimento ocurre varias veces en condiciones similares, si no produce el mismo resultado cada vez, pero el resultado en un ensayo es uno de los varios resultados posibles, entonces dicho experimento se llama evento aleatorio o un evento probabilístico.
- Evento elemental: el evento elemental se refiere al resultado de cada evento aleatorio realizado. Siempre que se realiza el evento aleatorio, cada resultado asociado se conoce como evento elemental.
- Espacio de muestra: el espacio de muestra se refiere al conjunto de todos los resultados posibles de un evento aleatorio. Por ejemplo, cuando se lanza una moneda, los resultados posibles son cara y cruz.
- Evento: un evento se refiere al subconjunto del espacio muestral asociado con un evento aleatorio.
- Ocurrencia de un evento: se dice que ocurre un evento asociado con un evento aleatorio si cualquiera de los eventos elementales que le pertenecen es un resultado.
- Evento seguro: se dice que un evento asociado con un evento aleatorio es un evento seguro si siempre ocurre cada vez que se realiza el evento aleatorio.
- Evento imposible: se dice que un evento asociado con un evento aleatorio es un evento imposible si nunca ocurre cada vez que se realiza el evento aleatorio.
- Evento compuesto: se dice que un evento asociado con un evento aleatorio es un evento compuesto si es la unión separada de dos o más eventos elementales.
- Eventos mutuamente excluyentes: se dice que dos o más eventos asociados con un evento aleatorio son eventos mutuamente excluyentes si cualquiera de los eventos ocurre, evita la ocurrencia de todos los demás eventos. Esto significa que no pueden ocurrir dos o más eventos simultáneamente Mismo tiempo.
- Eventos exhaustivos: se dice que dos o más eventos asociados con un evento aleatorio son eventos exhaustivos si su unión es el espacio muestral.
Probabilidad de un evento: si hay un total de p resultados posibles asociados con un experimento aleatorio y q de ellos son resultados favorables para el evento A, entonces la probabilidad del evento A se denota por P(A) y viene dada por
P(A) = q/p
La probabilidad de que no ocurra el evento A, es decir, P(A’) = 1 – P(A)
Nota –
- Si el valor de P(A) = 1, entonces el evento A se llama evento seguro.
- Si el valor de P(A) = 0, entonces el evento A se llama evento imposible.
- Además, P(A) + P(A’) = 1
Teoremas:
- General – Sean A, B, C los eventos asociados con un experimento aleatorio, entonces
- P(A∪B) = P(A) + P(B) – P(A∩B)
- P(A∪B) = P(A) + P(B) si A y B son mutuamente excluyentes
- P(A∪B∪C) = P(A) + P(B) + P(C) – P(A∩B) – P(B∩C)- P(C∩A) + P(A∩B) ∩C)
- P(A∩B’) = P(A) – P(A∩B)
- P(A’∩B) = P(B) – P(A∩B)
- Extensión del Teorema de la Multiplicación – Sean A 1 , A 2 , ….., A n n eventos asociados con un experimento aleatorio, entonces P(A 1 ∩A 2 ∩A 3 ….. A n ) = P(A 1 ) P(A 2 /A 1 )P(A 3 /A 2 ∩A 1 ) ….. P(A n /A 1 ∩A 2 ∩A 3 ∩ ….. ∩A n-1 )
Ley de Probabilidad Total – Sea S el espacio muestral asociado con un experimento aleatorio y E 1 , E 2 , …, E n sean eventos mutuamente excluyentes y exhaustivos asociados con el experimento aleatorio. Si A es cualquier evento que ocurre con E 1 o E 2 o … o E n , entonces
P(A) = P(E1)P(A/E1) + P(E2)P(A/E2) + ... + P(En)P(A/En)
La probabilidad condicional P(A | B) indica la probabilidad de que suceda el evento ‘A’ dado que sucedió el evento B.
Regla del producto:
derivada de la definición anterior de probabilidad condicional al multiplicar ambos lados por P(B)
P(A ∩ B) = P(B) * P(A|B)
Variables
aleatorias Una variable aleatoria es básicamente una función que mapea del conjunto del espacio muestral al conjunto de números reales. El propósito es tener una idea sobre el resultado de una situación particular en la que se nos dan probabilidades de diferentes resultados.
Distribución de probabilidad discreta: si las probabilidades se definen en una variable aleatoria discreta, que solo puede tomar un conjunto discreto de valores, entonces se dice que la distribución es una distribución de probabilidad discreta.
Distribución de probabilidad continua: si las probabilidades se definen en una variable aleatoria continua, que puede tomar cualquier valor entre dos números, se dice que la distribución es una distribución de probabilidad continua.
Función de distribución acumulativa:
similar a la función de densidad de probabilidad, la función de distribución acumulativa ![]() de una variable aleatoria X de valor real, o simplemente la función de distribución
de una variable aleatoria X de valor real, o simplemente la función de distribución ![]() evaluada en
evaluada en ![]() , es la probabilidad que
, es la probabilidad que ![]() tomará un valor menor o igual que
tomará un valor menor o igual que ![]() .
.
Para una variable aleatoria discreta, ![]()
para una variable aleatoria continua, 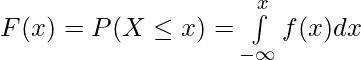
Distribución de probabilidad uniforme –
La Distribución Uniforme, también conocida como Distribución Rectangular , es un tipo de Distribución de Probabilidad Continua.
Tiene una Variable Aleatoria Continua ![]() restringida a un intervalo finito
restringida a un intervalo finito ![]() y su función de probabilidad
y su función de probabilidad ![]() tiene una densidad constante sobre este intervalo.
tiene una densidad constante sobre este intervalo.
La función de distribución de probabilidad uniforme se define como-
![Rendered by QuickLaTeX.com \[ f(x) = \begin{cases} \frac{1}{b-a}, & a\leq x \leq b\\ 0, & \text{otherwise}\\ \end{cases} \]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-306dafe287bd4312c20cf4b1b56295c5_l3.png)
Expectativa: La media de la distribución, representada como E[x]. ![Rendered by QuickLaTeX.com E(x) = \int \limits_{-\infty}^{\infty} xf(x) dx\\ or, E[x]=\sum xP(x)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bdcd21e8451367e42a805fd1a6e5af3a_l3.png)
Varianza: ![]() .
.
Para una distribución uniforme, ![]()
![]()
Distribución exponencial
Para un número real positivo, ![]() la función de densidad de probabilidad de una variable aleatoria distribuida exponencialmente está dada por:
la función de densidad de probabilidad de una variable aleatoria distribuida exponencialmente está dada por:
![Rendered by QuickLaTeX.com f_X(x) = \[ \begin{cases} \lambda e^{-\lambda x} & if x\in R_X \\ 0 & if x \notin R_X \end{cases} \]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3b2925174fef5babfee67e72a8a1daf0_l3.png)
donde R x son variables aleatorias exponenciales. ![]()
![]()
Distribución Binomial: ![]()
Media =np, donde p es la probabilidad de éxito
Varianza . = np(1-p)
Cálculo:
Límites, Continuidad y Diferenciabilidad
Existencia de límite: el límite de una función ![]() en
en ![]() existe solo cuando su límite izquierdo y su límite derecho existen y son iguales, es decir
existe solo cuando su límite izquierdo y su límite derecho existen y son iguales, es decir ![]()
Algunos límites comunes –

Regla de L’Hospital –
Si el límite dado ![]() es de la forma
es de la forma ![]() o
o ![]() es decir, ambos
es decir, ambos ![]() y
y ![]() son 0 o ambos
son 0 o ambos ![]() y
y ![]() son
son ![]() , entonces el límite puede resolverse mediante la regla de L’Hospital .
, entonces el límite puede resolverse mediante la regla de L’Hospital .
Si el límite es de la forma descrita arriba, entonces la regla de L’Hospital dice que – ![]()
donde ![]() y se
y se ![]() obtiene al derivar
obtiene al derivar ![]() y
y ![]() .
.
Si después de la diferenciación, el formulario aún existe, entonces la regla se puede aplicar continuamente hasta que se cambie el formulario.
Continuidad
Se dice que una función es continua en un rango si su gráfico es una sola curva continua.
Formalmente, se dice que una
función de valor real ![]() es continua en un punto
es continua en un punto ![]() del dominio si –
del dominio si – ![]() existe y es igual a
existe y es igual a ![]() .
.
Si una función ![]() es continua en
es continua en ![]() entonces-
entonces- ![]()
Se dice que las funciones que no son continuas son discontinuas.
Diferenciabilidad
La derivada de una función de valor real ![]() wrt
wrt ![]() es la función
es la función ![]() y se define como:
y se define como: ![]()
Se dice que una función es diferenciable si la derivada de la función existe en todos los puntos de su dominio. Para comprobar la diferenciabilidad de una función en el punto ![]() ,
, ![]() debe existir.
debe existir.
Si una función es diferenciable en un punto, entonces también es continua en ese punto.
Nota – Si una función es continua en un punto no implica que la función también sea derivable en ese punto. Por ejemplo, ![]() es continua en
es continua en ![]() ese punto pero no es diferenciable.
ese punto pero no es diferenciable.
Teorema del valor medio de Lagrange
Supongamos que ![]() es una función que satisface tres condiciones:
es una función que satisface tres condiciones:
1) f(x) es continua en el intervalo cerrado a ≤ x ≤ b
2) f(x) es diferenciable en el intervalo abierto a < x < b
Entonces, de acuerdo con el Teorema de Lagrange, existe al menos un punto ‘c’ en el intervalo abierto (a, b) tal que:
![]()
Teorema del valor medio de Rolle
Supongamos que f(x) es una función que cumple tres condiciones:
1) f(x) es continua en el intervalo cerrado a ≤ x ≤ b
2) f(x) es diferenciable en el intervalo abierto a < x < b
3) f(a) = f(b)
Entonces, de acuerdo con el Teorema de Rolle, existe al menos un punto ‘c’ en el intervalo abierto (a, b) tal que:
f'(c) = 0
- Definición: Sea f(x) una función. Entonces la familia de todas sus antiderivadas se llama integral indefinida de una función f(x) y se denota por ∫f(x)dx.
El símbolo ∫f(x)dx se lee como la integral indefinida de f(x) con respecto a x.
Por lo tanto, ∫f(x)dx= ∅(x) + C.
Por lo tanto, el proceso de encontrar la integral indefinida de una función se llama integración de la función.
Fórmulas fundamentales de integración –
- ∫x norte dx = (x norte +1 /( n +1))+C
- ∫(1/x)dx = (log e |x|)+C
- ∫e x dx = (e x )+C
- ∫a x dx = (( ax )/(log e a))+C
- ∫sen(x)dx = -cos(x)+C
- ∫cos(x)dx = sen(x)+C
- ∫seg 2 (x)dx = tan(x)+C
- ∫coseg 2 (x)dx = -cot(x)+C
- ∫sec(x)tan(x)dx = sec(x)+C
- ∫cosec(x)cot(x)dx = -cosec(x)+C
- ∫cot(x)dx = log|sen(x)|+C
- ∫tan(x)dx = log|seg(x)|+C
- ∫sec(x)dx = log|sec(x)+tan(x)|+C
- ∫cosec(x)dx = log|cosec(x)-cot(x)|+C
Integrales definidas:
Las integrales definidas son la extensión después de las integrales indefinidas, las integrales definidas tienen límites [a, b]. Da el área de una curva delimitada entre límites dados.
![]() , It denotes the area of curve F(x) bounded between a and b, where a is the lower limit and b is the upper limit.
, It denotes the area of curve F(x) bounded between a and b, where a is the lower limit and b is the upper limit.
Nota: Si f es una función continua definida en el intervalo cerrado [a, b] y F es una antiderivada de f. Entonces ![]()
Aquí, la función f debe estar bien definida y ser continua en [a, b].
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA