Número de componentes conectados de un gráfico (usando Disjoint Set Union)

Dado un grafo no dirigido G con vértices numerados en el rango [0, N] y una array Edges[][] que consiste en M aristas, la tarea es encontrar el número total de componentes conectados en el gráfico usando el algoritmo Disjoint Set Union .

Ejemplos:

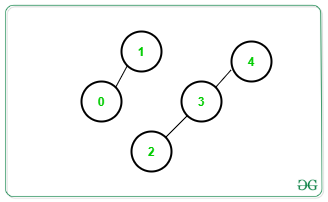
Entrada: N = 4, Edges[][] = {{1, 0}, {2, 3}, {3, 4}}
Salida: 2
Explicación: Solo hay 2 componentes conectados como se muestra a continuación:

Entrada: N = 4, Edges[][] = {{1, 0}, {0, 2}, {3, 5}, {3, 4}, {6, 7}}
Salida: 3
Explicación: Hay solo 3 componentes conectados como se muestra a continuación:

Enfoque: El problema se puede resolver utilizando el algoritmo Disjoint Set Union . Siga los pasos a continuación para resolver el problema:

• En el algoritmo DSU , hay dos funciones principales, es decir, la función connect() y root() .
• connect(): Conecta un borde.
• root(): determina recursivamente el padre superior de un borde dado.
• Para cada borde {a, b}, verifique si a está conectado con b o no. Si se encuentra que es falso, conéctelos agregando sus principales padres.
• Después de completar el paso anterior para cada borde, imprima el número total de los distintos padres superiores para cada vértice.

A continuación se muestra la implementación del enfoque anterior:

// C++ program for the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Stores the parent of each vertex
int parent[1000000];
 
// Function to find the topmost
// parent of vertex a
int root(int a)
{
    // If current vertex is
    // the topmost vertex
    if (a == parent[a]) {
        return a;
    }
 
    // Otherwise, set topmost vertex of
    // its parent as its topmost vertex
    return parent[a] = root(parent[a]);
}
 
// Function to connect the component
// having vertex a with the component
// having vertex b
void connect(int a, int b)
{
    // Connect edges
    a = root(a);
    b = root(b);
 
    if (a != b) {
        parent[b] = a;
    }
}
 
// Function to find unique top most parents
void connectedComponents(int n)
{
    set<int> s;
 
    // Traverse all vertices
    for (int i = 0; i < n; i++) {
 
        // Insert all topmost
        // vertices obtained
        s.insert(root(parent[i]));
    }
 
    // Print count of connected components
    cout << s.size() << '\n';
}
 
// Function to print answer
void printAnswer(int N,
                 vector<vector<int> > edges)
{
 
    // Setting parent to itself
    for (int i = 0; i <= N; i++) {
        parent[i] = i;
    }
 
    // Traverse all edges
    for (int i = 0; i < edges.size(); i++) {
        connect(edges[i][0], edges[i][1]);
    }
 
    // Print answer
    connectedComponents(N);
}
 
// Driver Code
int main()
{
    // Given N
    int N = 8;
 
    // Given edges
    vector<vector<int> > edges = {
        { 1, 0 }, { 0, 2 }, { 5, 3 }, { 3, 4 }, { 6, 7 }
    };
 
    // Function call
    printAnswer(N, edges);
 
    return 0;
}

// Java program for the above approach
import java.util.*;
class GFG{
 
// Stores the parent of each vertex
static int []parent = new int[1000000];
 
// Function to find the topmost
// parent of vertex a
static int root(int a)
{
   
    // If current vertex is
    // the topmost vertex
    if (a == parent[a])
    {
        return a;
    }
 
    // Otherwise, set topmost vertex of
    // its parent as its topmost vertex
    return parent[a] = root(parent[a]);
}
 
// Function to connect the component
// having vertex a with the component
// having vertex b
static void connect(int a, int b)
{
   
    // Connect edges
    a = root(a);
    b = root(b);
 
    if (a != b) {
        parent[b] = a;
    }
}
 
// Function to find unique top most parents
static void connectedComponents(int n)
{
    HashSet<Integer> s = new HashSet<Integer>();
 
    // Traverse all vertices
    for (int i = 0; i < n; i++)
    {
 
        // Insert all topmost
        // vertices obtained
        s.add(parent[i]);
    }
 
    // Print count of connected components
    System.out.println(s.size());
}
 
// Function to print answer
static void printAnswer(int N,int [][] edges)
{
 
    // Setting parent to itself
    for (int i = 0; i <= N; i++)
    {
        parent[i] = i;
    }
 
    // Traverse all edges
    for (int i = 0; i < edges.length; i++)
    {
        connect(edges[i][0], edges[i][1]);
    }
 
    // Print answer
    connectedComponents(N);
}
 
// Driver Code
public static void main(String[] args)
{
   
    // Given N
    int N = 8;
 
    // Given edges
   int [][]edges = {{ 1, 0 }, { 0, 2 },
                    { 5, 3 }, { 3, 4 },
                    { 6, 7 }};
 
    // Function call
    printAnswer(N, edges);
}
}
 
// This code is contributed by 29AjayKumar

# Python3 program for the above approach
from collections import defaultdict
# Given N
N = 8
 
# Given edges
edges = [[1, 0 ], [ 0, 2 ], [ 5, 3 ], [ 3, 4 ], [ 6, 7 ]]
 
# Stores the parent of each vertex
parent = list(range(N))
  
# Function to find the topmost
# parent of vertex x
def find(x):
  if x != parent[x]:
    parent[x] = find(parent[x])
  return parent[x]
 
def union(x,y):
  parent_x = find(x)
  parent_y = find(y)
  if parent_x != parent_y:
    parent[parent_y] = parent_x
     
for x,y in edges:
  union(x,y)
 
dict_pair = defaultdict(list)
 
for idx, val in enumerate(parent):
  dict_pair[find(val)].append(idx)
 
print(len(dict_pair.keys()))
     
 
 
# This code is contributed by Shivam Dwivedi

// C# program for the above approach
using System;
using System.Collections.Generic;
class GFG {
     
    // Stores the parent of each vertex
    static int[] parent = new int[1000000];
       
    // Function to find the topmost
    // parent of vertex a
    static int root(int a)
    {
        // If current vertex is
        // the topmost vertex
        if (a == parent[a]) {
            return a;
        }
       
        // Otherwise, set topmost vertex of
        // its parent as its topmost vertex
        return parent[a] = root(parent[a]);
    }
       
    // Function to connect the component
    // having vertex a with the component
    // having vertex b
    static void connect(int a, int b)
    {
        // Connect edges
        a = root(a);
        b = root(b);
       
        if (a != b) {
            parent[b] = a;
        }
    }
       
    // Function to find unique top most parents
    static void connectedComponents(int n)
    {
        HashSet<int> s = new HashSet<int>();
       
        // Traverse all vertices
        for (int i = 0; i < n; i++) {
       
            // Insert all topmost
            // vertices obtained
            s.Add(parent[i]);
        }
       
        // Print count of connected components
        Console.WriteLine(s.Count);
    }
       
    // Function to print answer
    static void printAnswer(int N, List<List<int> > edges)
    {
       
        // Setting parent to itself
        for (int i = 0; i <= N; i++) {
            parent[i] = i;
        }
       
        // Traverse all edges
        for (int i = 0; i < edges.Count; i++) {
            connect(edges[i][0], edges[i][1]);
        }
       
        // Print answer
        connectedComponents(N);
    }  
 
  // Driver code
  static void Main() {
       
    // Given N
    int N = 8;
   
    // Given edges
    List<List<int>> edges = new List<List<int>>();
    edges.Add(new List<int> { 1, 0 });
    edges.Add(new List<int> { 0, 2 });
    edges.Add(new List<int> { 5, 3 });
    edges.Add(new List<int> { 3, 4 });
    edges.Add(new List<int> { 6, 7 });
   
    // Function call
    printAnswer(N, edges);
  }
}
 
// This code is contributed by divyeshrabadiya07

<script>
 
// Javascript program for the above approach
 
// Stores the parent of each vertex
var parent = Array(1000000);
 
// Function to find the topmost
// parent of vertex a
function root(a)
{
    // If current vertex is
    // the topmost vertex
    if (a == parent[a]) {
        return a;
    }
 
    // Otherwise, set topmost vertex of
    // its parent as its topmost vertex
    return parent[a] = root(parent[a]);
}
 
// Function to connect the component
// having vertex a with the component
// having vertex b
function connect( a, b)
{
    // Connect edges
    a = root(a);
    b = root(b);
 
    if (a != b) {
        parent[b] = a;
    }
}
 
// Function to find unique top most parents
function connectedComponents( n)
{
    var s = new Set();
 
    // Traverse all vertices
    for (var i = 0; i < n; i++) {
 
        // Insert all topmost
        // vertices obtained
        s.add(parent[i]);
    }
 
    // Print count of connected components
    document.write( s.size + "<br>");
}
 
// Function to print answer
function printAnswer( N, edges)
{
 
    // Setting parent to itself
    for (var i = 0; i <= N; i++) {
        parent[i] = i;
    }
 
    // Traverse all edges
    for (var i = 0; i < edges.length; i++) {
        connect(edges[i][0], edges[i][1]);
    }
 
    // Print answer
    connectedComponents(N);
}
 
// Driver Code
// Given N
var N = 8;
// Given edges
var edges = [
    [ 1, 0 ], [ 0, 2 ], [ 5, 3 ], [ 3, 4 ], [ 6, 7 ]
];
 
// Function call
printAnswer(N, edges);
 
 
</script>

3

Complejidad de Tiempo: O(NLOGN+M)
Espacio Auxiliar: O(N+M)