Dado un número entero n > 0, que denota el número de dígitos, la tarea de encontrar el número total de números enteros positivos de n dígitos que no son de naturaleza decreciente.
Un entero no decreciente es aquel en el que todos los dígitos de izquierda a derecha están en forma no decreciente. ej: 1234, 1135, ..etc.
Nota: Los ceros iniciales también cuentan en números enteros no decrecientes, como 0000, 0001, 0023, etc., que también son números enteros no decrecientes de 4 dígitos.
Ejemplos:
Input : n = 1 Output : 10 Numbers are 0, 1, 2, ...9. Input : n = 2 Output : 55 Input : n = 4 Output : 715
Enfoque ingenuo: generamos todos los números posibles de n dígitos y luego, para cada número, verificamos si no es decreciente o no.
Complejidad de tiempo: (n*10^n), donde 10^n es para generar todos los números de n dígitos posibles y n es para verificar si un número en particular no es decreciente o no.
Programación Dinámica:
Si llenamos dígitos uno por uno de izquierda a derecha, se cumplen las siguientes condiciones.
- Si el último dígito actual es 9, podemos completar solo 9 en los lugares restantes. Entonces, solo es posible una solución si el último dígito actual es 9.
- Si el último dígito actual es menor que 9, entonces podemos calcular recursivamente el conteo usando la siguiente fórmula.
a[i][j] = a[i-1][j] + a[i][j + 1]
For every digit j smaller than 9.
We consider previous length count and count
to be increased by all greater digits.
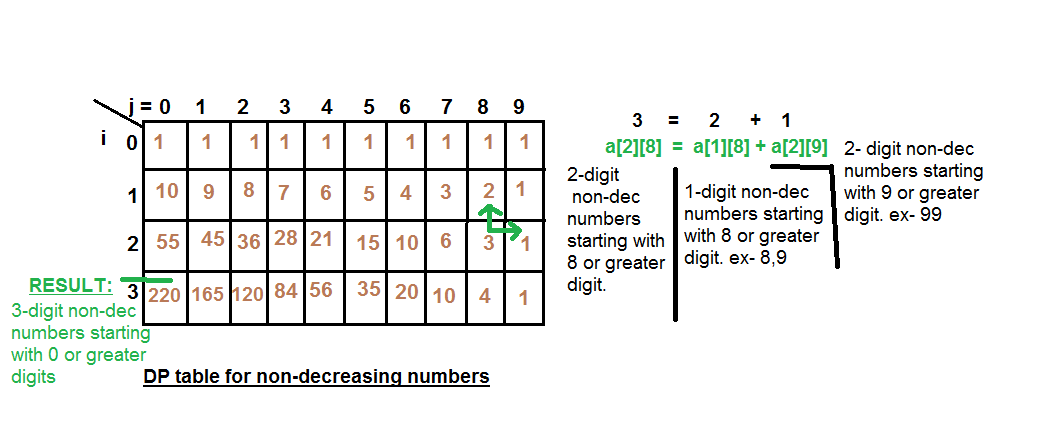
Construimos una array a[][] donde a[i][j] = recuento de todos los enteros no decrecientes de i-dígito válidos con j o mayor que j como dígito inicial. La solución se basa en las siguientes observaciones. Llenamos esta array por columnas, primero calculando a[1][9] y luego usando este valor para calcular a[2][8] y así sucesivamente.
En cualquier momento, si deseamos calcular a[i][j] significa el número de i-dígitos enteros no decrecientes con el dígito inicial como j o un dígito mayor que j, debemos sumar a[i-1][j] ( número de enteros de i-1 dígito que deben comenzar desde j o un dígito mayor, porque en este caso si colocamos j como su dígito más a la izquierda, entonces nuestro número será i-dígito número no decreciente) y a[i][j+ 1] (número de enteros i-dígito que deben comenzar con un dígito igual a mayor que j+1). Entonces, a[i][j] = a[i-1][j] + a[i][j+1].
C++
// C++ program for counting n digit numbers with
// non decreasing digits
#include <bits/stdc++.h>
using namespace std;
// Returns count of non- decreasing numbers with
// n digits.
int nonDecNums(int n)
{
/* a[i][j] = count of all possible number
with i digits having leading digit as j */
int a[n + 1][10];
// Initialization of all 0-digit number
for (int i = 0; i <= 9; i++)
a[0][i] = 1;
/* Initialization of all i-digit
non-decreasing number leading with 9*/
for (int i = 1; i <= n; i++)
a[i][9] = 1;
/* for all digits we should calculate
number of ways depending upon leading
digits*/
for (int i = 1; i <= n; i++)
for (int j = 8; j >= 0; j--)
a[i][j] = a[i - 1][j] + a[i][j + 1];
return a[n][0];
}
// driver program
int main()
{
int n = 2;
cout << "Non-decreasing digits = "
<< nonDecNums(n) << endl;
return 0;
}
Java
// Java program for counting n digit numbers with
// non decreasing digits
import java.io.*;
class GFG {
// Function that returns count of non- decreasing numbers
// with n digits
static int nonDecNums(int n)
{
// a[i][j] = count of all possible number
// with i digits having leading digit as j
int[][] a = new int[n + 1][10];
// Initialization of all 0-digit number
for (int i = 0; i <= 9; i++)
a[0][i] = 1;
// Initialization of all i-digit
// non-decreasing number leading with 9
for (int i = 1; i <= n; i++)
a[i][9] = 1;
// for all digits we should calculate
// number of ways depending upon leading
// digits
for (int i = 1; i <= n; i++)
for (int j = 8; j >= 0; j--)
a[i][j] = a[i - 1][j] + a[i][j + 1];
return a[n][0];
}
// driver program
public static void main(String[] args)
{
int n = 2;
System.out.println("Non-decreasing digits = " + nonDecNums(n));
}
}
// Contributed by Pramod Kumar
Python3
# Python3 program for counting n digit
# numbers with non decreasing digits
import numpy as np
# Returns count of non- decreasing
# numbers with n digits.
def nonDecNums(n) :
# a[i][j] = count of all possible number
# with i digits having leading digit as j
a = np.zeros((n + 1, 10))
# Initialization of all 0-digit number
for i in range(10) :
a[0][i] = 1
# Initialization of all i-digit
# non-decreasing number leading with 9
for i in range(1, n + 1) :
a[i][9] = 1
# for all digits we should calculate
# number of ways depending upon
# leading digits
for i in range(1, n + 1) :
for j in range(8, -1, -1) :
a[i][j] = a[i - 1][j] + a[i][j + 1]
return int(a[n][0])
# Driver Code
if __name__ == "__main__" :
n = 2
print("Non-decreasing digits = ",
nonDecNums(n))
# This code is contributed by Ryuga
C#
// C# function to find number of diagonals
// in n sided convex polygon
using System;
class GFG {
// Function that returns count of non-
// decreasing numbers with n digits
static int nonDecNums(int n)
{
// a[i][j] = count of all possible number
// with i digits having leading digit as j
int[, ] a = new int[n + 1, 10];
// Initialization of all 0-digit number
for (int i = 0; i <= 9; i++)
a[0, i] = 1;
// Initialization of all i-digit
// non-decreasing number leading with 9
for (int i = 1; i <= n; i++)
a[i, 9] = 1;
// for all digits we should calculate
// number of ways depending upon leading
// digits
for (int i = 1; i <= n; i++)
for (int j = 8; j >= 0; j--)
a[i, j] = a[i - 1, j] + a[i, j + 1];
return a[n, 0];
}
// driver program
public static void Main()
{
int n = 2;
Console.WriteLine("Non-decreasing digits = " +
nonDecNums(n));
}
}
// This code is contributed by Sam007
PHP
<?php
// PHP program for counting
// n digit numbers with
// non decreasing digits
// Returns count of non-
// decreasing numbers with
// n digits.
function nonDecNums($n)
{
/* a[i][j] = count of
all possible number
with i digits having
leading digit as j */
// Initialization of
// all 0-digit number
for ($i = 0; $i <= 9; $i++)
$a[0][$i] = 1;
/* Initialization of all
i-digit non-decreasing
number leading with 9*/
for ($i = 1; $i <= $n; $i++)
$a[$i][9] = 1;
/* for all digits we should
calculate number of ways
depending upon leading digits*/
for ($i = 1; $i <= $n; $i++)
for ($j = 8; $j >= 0; $j--)
$a[$i][$j] = $a[$i - 1][$j] +
$a[$i][$j + 1];
return $a[$n][0];
}
// Driver Code
$n = 2;
echo "Non-decreasing digits = ",
nonDecNums($n),"\n";
// This code is contributed by m_kit
?>
Javascript
<script>
// Javascript program for counting n digit
// numbers with non decreasing digits
// Function that returns count
// of non- decreasing numbers
// with n digits
function nonDecNums(n)
{
// a[i][j] = count of all possible number
// with i digits having leading digit as j
let a = new Array(n + 1)
for (let i = 0; i < n + 1; i++)
{
a[i] = new Array(10);
}
// Initialization of all 0-digit number
for (let i = 0; i <= 9; i++)
a[0][i] = 1;
// Initialization of all i-digit
// non-decreasing number leading with 9
for (let i = 1; i <= n; i++)
a[i][9] = 1;
// for all digits we should calculate
// number of ways depending upon leading
// digits
for (let i = 1; i <= n; i++)
for (let j = 8; j >= 0; j--)
a[i][j] = a[i - 1][j] + a[i][j + 1];
return a[n][0];
}
let n = 2;
document.write(
"Non-decreasing digits = " + nonDecNums(n)
);
</script>
Non-decreasing digits = 55
Producción :
Non-decreasing digits = 55
Complejidad temporal: O(10*n) equivalente a O(n).
Otro enfoque:
Si observamos, podemos ver que el 0 debe colocarse antes del 1-9, el 1 debe colocarse antes del 2-9 y así sucesivamente. Como se nos pide encontrar números enteros no decrecientes, 111223 es un número entero no decreciente válido, lo que significa que el mismo dígito puede aparecer consecutivamente.

Ejemplo 1 : Cuando N=2, tenemos 11C9, que es igual a 55.
Ejemplo 2 : Cuando N=5, tenemos 14C9, que es igual a 2002.
C++
// CPP program To calculate Number of n-digits non-decreasing integers
//Contributed by Parishrut Kushwaha//
#include <bits/stdc++.h>
using namespace std;
// Returns factorial of n
long long int fact(int n)
{
long long int res = 1;
for (int i = 2; i <= n; i++)
res = res * i;
return res;
}
// returns nCr
long long int nCr(int n, int r)
{
return fact(n) / (fact(r) * fact(n - r));
}
// Driver code
int main()
{
int n = 2;
cout <<"Number of Non-Decreasing digits: "<< nCr(n+9,9);
return 0;
}
Java
// Java program To calculate Number
// of n-digits non-decreasing integers
class GFG {
// Returns factorial of n
static long fact(int n)
{
long res = 1;
for (int i = 2; i <= n; i++)
res = res * i;
return res;
}
// returns nCr
static long nCr(int n, int r)
{
return fact(n) / (fact(r) * fact(n - r));
}
// Driver code
public static void main(String[] args)
{
int n = 2;
System.out.println(
"Number of Non-Decreasing digits: "
+ nCr(n + 9, 9));
}
}
// This code is contributed by rajsanghavi9.
Python3
# Python program To calculate Number of n-digits non-decreasing integers
#Contributed by Parishrut Kushwaha#
# Returns factorial of n
def fact(n):
res = 1
for i in range (2,n+1):
res = res * i
return res
# returns nCr
def nCr(n, r):
return fact(n) // ((fact(r) * fact(n - r)))
# Driver code
n = 2
print("Number of Non-Decreasing digits: " , nCr(n+9,9))
# This code is contributed by shivanisinghss2110
C#
// C# program To calculate Number
// of n-digits non-decreasing integers
using System;
class GFG {
// Returns factorial of n
static long fact(int n)
{
long res = 1;
for (int i = 2; i <= n; i++)
res = res * i;
return res;
}
// returns nCr
static long nCr(int n, int r)
{
return fact(n) / (fact(r) * fact(n - r));
}
// Driver code
public static void Main(String[] args)
{
int n = 2;
Console.Write("Number of Non-Decreasing digits: " + nCr(n + 9, 9));
}
}
// This code is contributed by shivanisinghss2110
Javascript
<script>
// JavaScript program To calculate Number
// of n-digits non-decreasing integers
// Returns factorial of n
function fact( n)
{
var res = 1;
for (var i = 2; i <= n; i++)
res = res * i;
return res;
}
// returns nCr
function nCr(n, r)
{
return fact(n) / (fact(r) * fact(n - r));
}
// Driver code
var n = 2;
document.write("Number of Non-Decreasing digits: " + nCr(n + 9, 9));
// This code is contributed by shivanisinghss2110.
</script>
Number of Non-Decreasing digits: 55
Complejidad temporal: O(n).
Complejidad espacial: O(n) .
Este artículo es una contribución de Shivam Pradhan (anuj_charm) . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA