Dado un balón de fútbol estándar, se dibujan hexágonos y pentágonos regulares como se muestra en la imagen. Calcula el número de hexágonos y pentágonos.

Podemos aplicar las características de Euler para averiguar el número de hexágonos y pentágonos en un balón de fútbol estándar.
Según las Características de Euler: Para toda superficie S existe un número entero
![]()
tal que siempre que un grafo G con V vértices y E aristas se incrusta en S de modo que haya F caras (regiones divididas por el grafo), tenemos:
![]()
Para una esfera (forma de balón de fútbol)
![]()
= 2.
Por lo tanto, la ecuación se convierte en V – E + F = 2.
Ahora, sea el número de pentágonos P y el número de hexágonos H.
El número de vértices será:
6 vértices por cada uno de los hexágonos, es decir 6*H.
5 vértices para cada uno de los pentágonos, es decir, 5*P.
Pero hemos contado cada vértice tres veces, una vez por cada polígono adyacente, sigue la imagen 
Por lo tanto, número de vértices, V = (6*H + 5*P)/3.
El número de aristas será:
6 aristas por cada uno de los hexágonos, es decir 6*H.
5 aristas para cada uno de los pentágonos, es decir, 5*P.
Pero hemos contado cada borde dos veces, una vez por cada polígono adyacente, sigue la imagen 
Por lo tanto, número de bordes, E = (6*H + 5*P)/2.
Número de caras será:
Hay H hexágonos y P pentágonos, cada uno formando una cara. Por lo tanto, número total de caras, F = (H + P).
Entonces, podemos escribir:
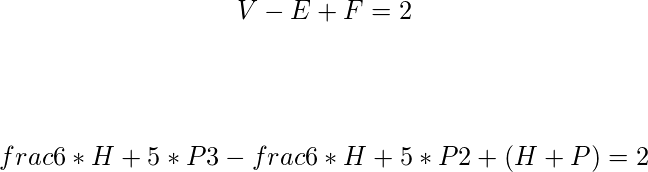
después de resolver esta ecuación obtendremos P = 12. Entonces, hay 12 pentágonos.
Ahora número de Hexágonos:
Podemos ver que cada pentágono está rodeado por 5 Hexágonos. Entonces debería haber 5*P hexágonos, pero hemos contado cada hexágono tres veces por cada uno de sus 3 pentágonos adyacentes. Por lo tanto, número de hexágonos = 5*P/3 = 5*12/3 = 20.
Por lo tanto, hay 20 hexágonos y 12 pentágonos en un balón de fútbol estándar.