Número de relaciones simétricas en un conjunto

Dado un número n, encuentra el número de Relaciones Simétricas en un conjunto de primeros n números naturales {1, 2, ..n}.

Ejemplos: 

Input  : n = 2
Output : 8
 
Given set is {1, 2}. Below are all symmetric relation.
{}
{(1, 1)}, 
{(2, 2)},
{(1, 1), (2, 2)}, 
{(1, 2), (2, 1)} 
{(1, 1), (1, 2), (2, 1)},
{(2, 2), (1, 2), (2, 1)}, 
{(1, 1), (2, 2), (2, 1), (1, 2)} 

Input  : n = 3
Output : 64

Se dice que una relación ‘R’ en el conjunto A es simétrica si xRy entonces yRx para todo x, y ∈ A 
o si (x, y) ∈ R, entonces (y, x) ∈ R para todo x, y?A 

El número total de relaciones simétricas es 2 ^n(n+1)/2 .
¿Cómo funciona esta fórmula?
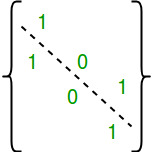
Una relación R es simétrica si el valor de cada celda (i, j) es el mismo que el de esa celda (j, i). Las diagonales pueden tener cualquier valor. 
 

Hay n valores diagonales, combinación total posible de valores diagonales = 2 ⁿ 
Hay n ² – n valores no diagonales. Solo podemos elegir un valor diferente para la mitad de ellos, porque cuando elegimos un valor para la celda (i, j), la celda (j, i) obtiene el mismo valor. 
Entonces combinación de valores no diagonales = 2 ^{(n2 – n)/2}
Combinación total = 2 ⁿ * 2 ^{(n2 – n)/2} = 2 ^n(n+1)/2
 

// C++ program to count total symmetric relations
// on a set of natural numbers.
#include <bits/stdc++.h>
 
// function find the square of n
unsigned int countSymmetric(unsigned int n)
{
    // Base case
    if (n == 0)
        return 1;
 
   // Return 2^(n(n + 1)/2)
   return 1 << ((n * (n + 1))/2);
}
 
// Driver code
int main()
{
    unsigned int n = 3;
 
    printf("%u", countSymmetric(n));
    return 0;
}

// Java program to count total symmetric
// relations on a set of natural numbers.
import java.io.*;
import java.util.*;
 
class GFG {
 
    // function find the square of n
    static int countSymmetric(int n)
    {
        // Base case
        if (n == 0)
            return 1;
     
    // Return 2^(n(n + 1)/2)
    return 1 << ((n * (n + 1)) / 2);
    }
 
    // Driver code
    public static void main (String[] args)
    {
        int n = 3;
        System.out.println(countSymmetric(n));
    }
}
 
 
// This code is contributed by Nikita Tiwari.

# Python 3 program to count
# total symmetric relations
# on a set of natural numbers.
 
# function find the square of n
def countSymmetric(n) :
    # Base case
    if (n == 0) :
        return 1
  
    # Return 2^(n(n + 1)/2)
    return (1 << ((n * (n + 1))//2))
 
  
# Driver code
 
n = 3
print(countSymmetric(n))
 
# This code is contributed
# by Nikita Tiwari.

// C# program to count total symmetric
// relations on a set of natural numbers.
using System;
 
class GFG {
 
    // function find the square of n
    static int countSymmetric(int n)
    {
        // Base case
        if (n == 0)
            return 1;
     
    // Return 2^(n(n + 1)/2)
    return 1 << ((n * (n + 1)) / 2);
    }
 
    // Driver code
    public static void Main ()
    {
        int n = 3;
        Console.WriteLine(countSymmetric(n));
    }
}
 
 
// This code is contributed by vt_m.

<?php
// PHP program to count total symmetric
// relations on a set of natural numbers.
 
// function find the square of n
function countSymmetric($n)
{
    // Base case
    if ($n == 0)
        return 1;
 
    // Return 2^(n(n + 1)/2)
    return 1 << (($n * ($n + 1))/2);
}
 
    // Driver code
    $n = 3;
    echo(countSymmetric($n));
     
// This code is contributed by vt_m.
?>

<script>
 
// JavaScript program to count total symmetric
// relations on a set of natural numbers.
 
// function find the square of n
    function countSymmetric(n)
    {
        // Base case
        if (n == 0)
            return 1;
       
    // Return 2^(n(n + 1)/2)
    return 1 << ((n * (n + 1)) / 2);
    }
   
 
// Driver Code
 
        let n = 3;
        document.write(countSymmetric(n));
        
</script>

64