Número de triacontágono

Dado un número N , la tarea es encontrar el N número del ^{Triacontágono} .
 

Un número de Triacontágono es una clase de número figurado. Tiene un polígono de 30 lados llamado triacontágono. El N-ésimo número triacontagonal cuenta el número 30 de puntos y todos los demás puntos están rodeados por una esquina compartida común y forman un patrón. Los primeros números de triacontagonol son 1, 30, 87, 172… 
 

Ejemplos: 
 

Entrada: N = 2 
Salida: 30 
Explicación: 
El segundo número de triacontagonol es 30. 
Entrada: N = 3 
Salida: 87 
 

Enfoque: El N-ésimo número triacontagonal viene dado por la fórmula:
 

• Enésimo término del polígono de s lados = 
   
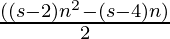
• Por lo tanto, el término N de un polígono de 30 lados es
   

A continuación se muestra la implementación del enfoque anterior: 
 

// C++ program for above approach
#include <bits/stdc++.h>
using namespace std;
 
// Finding the nth triacontagonal number
int triacontagonalNum(int n)
{
    return (28 * n * n - 26 * n) / 2;
}
 
// Driver code
int main()
{
    int n = 3;
     
    cout << "3rd triacontagonal Number is = "
         << triacontagonalNum(n);
 
    return 0;
}
 
// This code is contributed by shivanisinghss2110

// C program for above approach
#include <stdio.h>
#include <stdlib.h>
 
// Finding the nth triacontagonal Number
int triacontagonalNum(int n)
{
    return (28 * n * n - 26 * n) / 2;
}
 
// Driver program to test above function
int main()
{
    int n = 3;
    printf("3rd triacontagonal Number is = %d",
           triacontagonalNum(n));
 
    return 0;
}

// Java program for above approach
import java.io.*;
import java.util.*;
 
class GFG {
     
// Finding the nth triacontagonal number
static int triacontagonalNum(int n)
{
    return (28 * n * n - 26 * n) / 2;
}
 
// Driver code
public static void main(String[] args)
{
    int n = 3;
     
    System.out.println("3rd triacontagonal Number is = " +
                                    triacontagonalNum(n));
}
}
 
// This code is contributed by coder001

# Python3 program for above approach
 
# Finding the nth triacontagonal Number
def triacontagonalNum(n):
 
    return (28 * n * n - 26 * n) // 2
 
# Driver Code
n = 3
print("3rd triacontagonal Number is = ",
                   triacontagonalNum(n))
 
# This code is contributed by divyamohan123

// C# program for above approach
using System;
 
class GFG{
     
// Finding the nth triacontagonal number
static int triacontagonalNum(int n)
{
    return (28 * n * n - 26 * n) / 2;
}
 
// Driver code
public static void Main()
{
    int n = 3;
     
    Console.Write("3rd triacontagonal Number is = " +
                               triacontagonalNum(n));
}
}
 
// This code is contributed by Akanksha_Rai

<script>
 
 
// JavaScript program for above approach
 
// Finding the nth triacontagonal number
function triacontagonalNum(n)
{
    return (28 * n * n - 26 * n) / 2;
}
 
// Driver code
var n = 3;
document.write("3rd triacontagonal Number is = " + triacontagonalNum(n));
 
 
</script>

3rd triacontagonal Number is = 87

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)

Referencia: https://en.wikipedia.org/wiki/Triacontagon