Número mínimo de bordes necesarios para eliminar de un gráfico no dirigido para que sea acíclico

Dado un gráfico no dirigido que consta de N Nodes que contienen valores del rango [1, N] y M aristas en una array Edges[][] , la tarea es determinar el número mínimo de aristas que se deben eliminar para que el gráfico resultante no no contiene ningún ciclo .

Ejemplos:

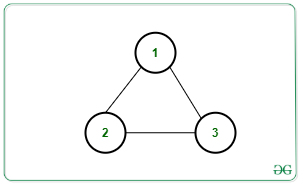
Entrada: N = 3, M = 3, bordes[][] = [[1, 2], [2, 3], [3, 1]]

Salida: 1
Explicación:
Eliminar cualquiera de los bordes hará que el gráfico sea acíclico. Por lo tanto, se debe eliminar al menos un borde.

Entrada: N = 3, M = 2, bordes[][] = [[1, 2], [2, 3]]

Salida: 0
Explicación: El gráfico ya es acíclico. Por lo tanto, no es necesario quitar los bordes.

Enfoque ingenuo: el enfoque más simple es intentar eliminar todas las combinaciones posibles de secuencias de bordes del gráfico dado uno por uno y, para cada combinación, contar el número de eliminaciones necesarias para que el gráfico sea acíclico. Finalmente, entre estas combinaciones, elija la que elimine el mínimo número de aristas para obtener un gráfico acíclico . Complejidad temporal: O(M!) Espacio auxiliar: O(N + M)

Enfoque eficiente: el enfoque anterior se puede optimizar en función de las siguientes observaciones:

Un grafo es acíclico cuando es un Árbol o un bosque de árboles (grupos de árboles desconectados).
Un árbol con Nodes C tendrá aristas ( C – 1 ).
Si hay K componentes conectados de C ₁ a C _K , entonces el número mínimo de aristas a eliminar es igual a:

METRO – (C ₁ – 1) – (C ₂ – 1) … (C _k -1 )
=> METRO – (C ₁ + … + C _K ) + K
=> METRO – N + K

Siga los pasos a continuación para resolver el problema:

Encuentre el número de componentes conectados del gráfico dado usando DFS .
Teniendo en cuenta que el recuento de componentes conectados es K , luego imprima M – N + K como el número mínimo requerido de bordes que se eliminarán para hacer que el gráfico resultante sea acíclico.

A continuación se muestra la implementación del enfoque anterior:

C++

// C++ Program to implement
// the above approach
 
#include <bits/stdc++.h>
using namespace std;
 
// Stores the adjacency list
vector<int> vec[100001];
 
// Stores if a vertex is
// visited or not
bool vis[100001];
int cc = 1;
 
// Function to perform DFS Traversal
// to count the number and size of
// all connected components
void dfs(int node)
{
    // Mark the current node as visited
    vis[node] = true;
 
    // Traverse the adjacency list
    // of the current node
    for (auto x : vec[node]) {
 
        // For every unvisited node
        if (!vis[x]) {
            cc++;
 
            // Recursive DFS Call
            dfs(x);
        }
    }
}
 
// Function to add undirected
// edge in the graph
void addEdge(int u, int v)
{
    vec[u].push_back(v);
    vec[v].push_back(u);
}
 
// Function to calculate minimum
// number of edges to be removed
void minEdgeRemoved(int N, int M,
                    int Edges[][2])
{
 
    // Create Adjacency list
    for (int i = 0; i < M; i++) {
        addEdge(Edges[i][0],
                Edges[i][1]);
    }
 
    memset(vis, false, sizeof(vis));
    int k = 0;
 
    // Iterate over all the nodes
    for (int i = 1; i <= N; i++) {
        if (!vis[i]) {
            cc = 1;
            dfs(i);
            k++;
        }
    }
 
    // Print the final count
    cout << M - N + k << endl;
}
 
// Driver Code
int main()
{
    int N = 3, M = 2;
 
    int Edges[][2] = { { 1, 2 }, { 2, 3 } };
 
    minEdgeRemoved(N, M, Edges);
}

Java

// Java program to implement
// the above approach
import java.util.*;
 
class GFG{
 
// Stores the adjacency list
@SuppressWarnings("unchecked")
static Vector<Integer> []vec = new Vector[100001];
 
// Stores if a vertex is
// visited or not
static boolean []vis = new boolean[100001];
static int cc = 1;
 
// Function to perform DFS Traversal
// to count the number and size of
// all connected components
static void dfs(int node)
{
     
    // Mark the current node as visited
    vis[node] = true;
 
    // Traverse the adjacency list
    // of the current node
    for(int x : vec[node])
    {
         
        // For every unvisited node
        if (!vis[x])
        {
            cc++;
 
            // Recursive DFS call
            dfs(x);
        }
    }
}
 
// Function to add undirected
// edge in the graph
static void addEdge(int u, int v)
{
    vec[u].add(v);
    vec[v].add(u);
}
 
// Function to calculate minimum
// number of edges to be removed
static void minEdgeRemoved(int N, int M,
                           int Edges[][])
{
     
    // Create Adjacency list
    for(int i = 0; i < M; i++)
    {
        addEdge(Edges[i][0],
                Edges[i][1]);
    }
 
    int k = 0;
 
    // Iterate over all the nodes
    for(int i = 1; i <= N; i++)
    {
        if (!vis[i])
        {
            cc = 1;
            dfs(i);
            k++;
        }
    }
 
    // Print the final count
    System.out.print(M - N + k + "\n");
}
 
// Driver Code
public static void main(String[] args)
{
    int N = 3, M = 2;
 
    int Edges[][] = { { 1, 2 }, { 2, 3 } };
     
    for(int i = 0; i < vec.length; i++)
        vec[i] = new Vector<Integer>();
         
    minEdgeRemoved(N, M, Edges);
}
}
 
// This code is contributed by 29AjayKumar

Python3

# Python3 program to implement
# the above approach
 
# Stores the adjacency list
vec = [[] for i in range(100001)]
 
# Stores if a vertex is
# visited or not
vis = [False] * 100001
cc = 1
 
# Function to perform DFS Traversal
# to count the number and size of
# all connected components
def dfs(node):
     
    global cc
     
    # Mark the current node as visited
    vis[node] = True
 
    # Traverse the adjacency list
    # of the current node
    for x in vec[node]:
 
        # For every unvisited node
        if (vis[x] == 0):
            cc += 1
 
            # Recursive DFS Call
            dfs(x)
 
# Function to add undirected
# edge in the graph
def addEdge(u, v):
     
    vec[u].append(v)
    vec[v].append(u)
 
# Function to calculate minimum
# number of edges to be removed
def minEdgeRemoved(N, M, Edges):
     
    global cc
 
    # Create Adjacency list
    for i in range(M):
        addEdge(Edges[i][0], Edges[i][1])
 
    # memset(vis, false, sizeof(vis))
    k = 0
 
    # Iterate over all the nodes
    for i in range(1, N + 1):
        if (not vis[i]):
            cc = 1
            dfs(i)
            k += 1
 
    # Print the final count
    print(M - N + k)
 
# Driver Code
if __name__ == '__main__':
     
    N = 3
    M = 2
 
    Edges = [ [ 1, 2 ], [ 2, 3 ] ]
 
    minEdgeRemoved(N, M, Edges)
 
# This code is contributed by mohit kumar 29

C#

// C# program to implement
// the above approach
using System;
using System.Collections.Generic;
 
class GFG{
 
// Stores the adjacency list
static List<int> []vec = new List<int>[100001];
 
// Stores if a vertex is
// visited or not
static bool []vis = new bool[100001];
static int cc = 1;
 
// Function to perform DFS Traversal
// to count the number and size of
// all connected components
static void dfs(int node)
{
     
    // Mark the current node as visited
    vis[node] = true;
 
    // Traverse the adjacency list
    // of the current node
    foreach(int x in vec[node])
    {
         
        // For every unvisited node
        if (!vis[x])
        {
            cc++;
 
            // Recursive DFS call
            dfs(x);
        }
    }
}
 
// Function to add undirected
// edge in the graph
static void addEdge(int u, int v)
{
    vec[u].Add(v);
    vec[v].Add(u);
}
 
// Function to calculate minimum
// number of edges to be removed
static void minEdgeRemoved(int N, int M,
                           int [,]Edges)
{
     
    // Create Adjacency list
    for(int i = 0; i < M; i++)
    {
        addEdge(Edges[i, 0],
                Edges[i, 1]);
    }
 
    int k = 0;
 
    // Iterate over all the nodes
    for(int i = 1; i <= N; i++)
    {
        if (!vis[i])
        {
            cc = 1;
            dfs(i);
            k++;
        }
    }
 
    // Print the readonly count
    Console.Write(M - N + k + "\n");
}
 
// Driver Code
public static void Main(String[] args)
{
    int N = 3, M = 2;
 
    int [,]Edges = { { 1, 2 }, { 2, 3 } };
     
    for(int i = 0; i < vec.Length; i++)
        vec[i] = new List<int>();
         
    minEdgeRemoved(N, M, Edges);
}
}
 
// This code is contributed by 29AjayKumar

Javascript

<script>
 
    // JavaScript implementation of the above approach
     
    // Stores the adjacency list
    let vec = new Array(100001);
 
    // Stores if a vertex is
    // visited or not
    let vis = new Array(100001);
    vis.fill(false);
    let cc = 1;
 
    // Function to perform DFS Traversal
    // to count the number and size of
    // all connected components
    function dfs(node)
    {
 
        // Mark the current node as visited
        vis[node] = true;
 
        // Traverse the adjacency list
        // of the current node
        for(let x = 0; x < vec[node].length; x++)
        {
 
            // For every unvisited node
            if (!vis[vec[node][x]])
            {
                cc++;
 
                // Recursive DFS call
                dfs(vec[node][x]);
            }
        }
    }
 
    // Function to add undirected
    // edge in the graph
    function addEdge(u, v)
    {
        vec[u].push(v);
        vec[v].push(u);
    }
 
    // Function to calculate minimum
    // number of edges to be removed
    function minEdgeRemoved(N, M, Edges)
    {
 
        // Create Adjacency list
        for(let i = 0; i < M; i++)
        {
            addEdge(Edges[i][0], Edges[i][1]);
        }
 
        let k = 0;
 
        // Iterate over all the nodes
        for(let i = 1; i <= N; i++)
        {
            if (!vis[i])
            {
                cc = 1;
                dfs(i);
                k++;
            }
        }
 
        // Print the readonly count
        document.write((M - N + k) + "</br>");
    }
     
    let N = 3, M = 2;
   
    let Edges = [ [ 1, 2 ], [ 2, 3 ] ];
       
    for(let i = 0; i < vec.length; i++)
        vec[i] = [];
           
    minEdgeRemoved(N, M, Edges);
     
</script>

Producción:

Complejidad temporal: O(N + M)
Espacio auxiliar: O(N + M)

Publicación traducida automáticamente

Artículo escrito por Srishtik Dutta y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

C++

Java

Python3

C#

Javascript

Deja una respuesta Cancelar la respuesta