Dadas dos arrays start[] y end[] que consisten en números enteros positivos que indican los puntos inicial y final de un segmento respectivamente, la tarea es encontrar el número mínimo de números enteros que se encuentra en al menos uno de los segmentos dados y cada segmento contiene al menos menos uno de ellos.
Ejemplos:
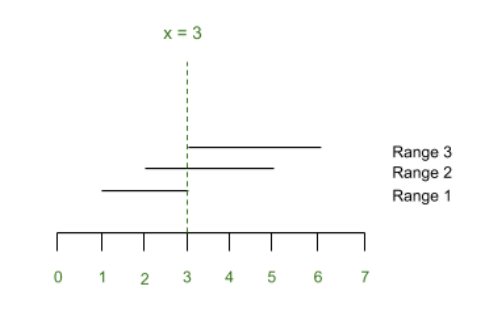
Entrada: start[] = {1, 2, 3}, end[] = { 3, 5, 6}
Salida: 3
Explicación:
Los tres rangos ([1, 3], [2, 5], [3, 6 ]) contiene el entero 3.Entrada: start[] = {4, 1, 2, 5}, end[] = {7, 3, 5, 6}
Salida: 3 6
Explicación:
Los segmentos {1, 3} y {2, 5} contienen el entero 3.
Los segmentos {4, 7} y {5, 6} contienen el entero 6.
Formulación matemática:
La forma matemática de describir el problema es considerar cada rango dado de números enteros como un segmento de línea definido por dos coordenadas enteras [a i , b i ] en una línea. Entonces, el número mínimo de enteros requeridos para cubrir cada uno del rango dado es el número mínimo de puntos tal que cada segmento contiene al menos un punto.
La representación del Ejemplo 1 se muestra a continuación:
Enfoque ingenuo:
la forma más sencilla de resolver el problema es encontrar el valor mínimo de todos los puntos iniciales y el valor máximo de todos los puntos finales de todos los segmentos. Iterar sobre este rango, y para cada punto en este rango, realizar un seguimiento de la cantidad de segmentos que se pueden cubrir usando este punto. Use una array para almacenar el número de segmentos como:
arr[punto] = número de segmentos que se pueden cubrir usando este punto
- Encuentre el valor máximo en la array arr[] .
- Si este valor máximo es igual a N, el índice correspondiente a este valor es el punto que cubre todos los segmentos.
- Si este valor máximo es menor que N , entonces el índice correspondiente a este valor es un punto que cubre algunos segmentos.
- Repita los pasos 1 a 3 para la array arr[] excluyendo este valor máximo hasta que la suma de todos los valores máximos encontrados sea igual a N.
Complejidad temporal: O((A-B+1)*N), donde A es el máximo de los puntos finales de los segmentos y B es el mínimo de los puntos iniciales de los segmentos.
Espacio Auxiliar: O(1)
Enfoque eficiente:
el problema se puede resolver de manera eficiente utilizando la técnica Greedy . Siga los pasos que se indican a continuación para resolver el problema:
- Ordena los segmentos por sus puntos finales.
- Seleccione el punto (o coordenada) correspondiente al punto final mínimo de todos los segmentos.
- Ahora, todos los segmentos cuyo punto de inicio sea menor que este punto seleccionado y cuyos puntos finales sean mayores que este punto seleccionado pueden ser cubiertos por este punto.
- Luego imprima el número mínimo de puntos.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// function to sort the 2D vector
// on basis of second element.
bool sortcol(const pair<int, int> p1,
const pair<int, int> p2)
{
return p1.second < p2.second;
}
// Function to compute minimum number
// of points which cover all segments
void minPoints(pair<int, int> points[], int n)
{
// Sort the list of tuples by
// their second element.
sort(points, points + n, sortcol);
// To store the solution
vector<int> coordinates;
int i = 0;
// Iterate over all the segments
while (i < n)
{
int seg = points[i].second;
coordinates.push_back(seg);
int p = i + 1;
if (p >= n)
break;
// Get the start point of next segment
int arrived = points[p].first;
// Loop over all those segments whose
// start point is less than the end
// point of current segment
while (seg >= arrived)
{
p += 1;
if (p >= n)
break;
arrived = points[p].first;
}
i = p;
}
// Print the possibles values of M
for(auto point : coordinates)
cout << point << " ";
}
// Driver code
int main()
{
int n = 4;
// Starting points of segments
int start[] = { 4, 1, 2, 5 };
// Ending points of segments
int end[] = { 7, 3, 5, 6 };
pair<int, int> points[n];
// Insert ranges in points[]
for(int i = 0; i < n; i++)
{
points[i] = { start[i], end[i] };
}
// Function call
minPoints(points, n);
return 0;
}
// This code is contributed by Kingash
Java
// Java program for the above approach
import java.util.*;
class GFG{
// Function to compute minimum number
// of points which cover all segments
static void minPoints(int[][] points, int n)
{
// Sort the list of tuples by
// their second element.
Arrays.sort(points, (a, b) -> a[1] - b[1]);
// To store the solution
ArrayList<Integer> coordinates = new ArrayList<>();
int i = 0;
// Iterate over all the segments
while (i < n)
{
int seg = points[i][1];
coordinates.add(seg);
int p = i + 1;
if (p >= n)
break;
// Get the start point of next segment
int arrived = points[p][0];
// Loop over all those segments whose
// start point is less than the end
// point of current segment
while (seg >= arrived)
{
p += 1;
if (p >= n)
break;
arrived = points[p][0];
}
i = p;
}
// Print the possibles values of M
for(Integer point : coordinates)
System.out.print(point + " ");
}
// Driver code
public static void main(String[] args)
{
int n = 4;
// Starting points of segments
int[] start = { 4, 1, 2, 5 };
// Ending points of segments
int[] end = { 7, 3, 5, 6 };
int[][] points = new int[n][2];
// Insert ranges in points[]
for(int i = 0; i < n; i++)
{
points[i][0] = start[i];
points[i][1] = end[i];
}
// Function call
minPoints(points, n);
}
}
// This code is contributed by offbeat
Python3
# Python3 program for the above approach # Function to compute minimum number # of points which cover all segments def minPoints(points): # Sort the list of tuples by # their second element. points.sort(key = lambda x: x[1]) # To store the solution coordinates = [] i = 0 # Iterate over all the segments while i < n: seg = points[i][1] coordinates.append(seg) p = i + 1 if p >= n: break # Get the start point of next segment arrived = points[p][0] # Loop over all those segments whose # start point is less than the end # point of current segment while seg >= arrived: p += 1 if p >= n: break arrived = points[p][0] i = p # Print the possibles values of M for point in coordinates: print(point, end =" ") # Driver Code n = 4 # Starting points of segments start = [4, 1, 2, 5] # Ending points of segments end = [7, 3, 5, 6] points = [] # Insert ranges in points[] for i in range(n): tu = (start[i], end[i]) points.append(tu) # Function Call minPoints(points)
Javascript
<script>
// JavaScript program for the above approach
// Function to compute minimum number
// of points which cover all segments
function minPoints(points){
// Sort the list of tuples by
// their second element.
points.sort((a,b)=>a[1]-b[1])
// To store the solution
let coordinates = []
let i = 0
// Iterate over all the segments
while(i < n){
let seg = points[i][1]
coordinates.push(seg)
let p = i + 1
if(p >= n)
break
// Get the start point of next segment
let arrived = points[p][0]
// Loop over all those segments whose
// start point is less than the end
// point of current segment
while(seg >= arrived){
p += 1
if(p >= n)
break
arrived = points[p][0]
}
i = p
}
// Print the possibles values of M
for(let point of coordinates)
document.write(point," ")
}
// Driver Code
let n = 4
// Starting points of segments
let start = [4, 1, 2, 5]
// Ending points of segments
let end = [7, 3, 5, 6]
let points = []
// Insert ranges in points[]
for(let i = 0; i < n; i++){
let tu = [start[i], end[i]]
points.push(tu)
}
// Function Call
minPoints(points)
// This code is contributed by shinjanpatra
</script>
3 6
Complejidad de tiempo: O(N*log N)
Espacio auxiliar: O(N)
Publicación traducida automáticamente
Artículo escrito por shivampatel5 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA