Dada una string S de longitud N y un arreglo A , que consta de letras minúsculas. También dado un número entero positivo K . la tarea es encontrar el número mínimo de intercambios requeridos (entre S y A) para hacer que la string S K sea periódica.
Nota:
- Se dice que una string es K periódica, si para cada posición i en la string S[i] = S[i+K] .
- En un movimiento, solo se puede intercambiar un carácter de S con un carácter de A.
- Los caracteres en A se pueden usar más de una vez.
Ejemplos:
Entrada: S = “nihsiakyt”, K = 3, A = [‘n’, ‘i’, ‘p’, ‘s’, ‘q’]
Salida: 6
Explicación:
considerando el posicionamiento basado en 0 para la string S:
Posiciones 3, 6 debe reemplazarse con ‘n’.
La posición 7 debe reemplazarse con ‘i’.
Las posiciones 2, 5, 8 se pueden reemplazar con cualquier carácter de A para hacer que la string K sea periódica.
3 strings periódicas finales: “nisnisnis”
Por lo tanto, se requieren intercambios mínimos = 6
Entrada: S = “abcdeactr”, K = 4, A = [‘a’, ‘c’, ‘p’]
Salida: 5
Explicación:
En total 5 cambios son necesarios para hacer la string 4 periódica.
Enfoque: este problema se puede resolver con la ayuda del recuento de frecuencias y el hash .
- Para resolver el problema mencionado anteriormente, usamos una array bidimensional freq[K][26] para almacenar la frecuencia de los caracteres en la posición j % K para todos
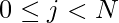 .
. - Use una array booleana para marcar todos los caracteres presentes en la array A.
- Para todos los caracteres en el rango de 0 a K habrá N / K o (N / K + 1) caracteres que deberían ser iguales.
- Entonces, para todos esos caracteres, verificamos qué carácter tiene la frecuencia máxima en la posición i y también está presente en la array A.
- Agregue eso a la respuesta, es decir
 .
. - También sumaremos 1 a la respuesta si
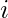
- porque habrá N / K + 1 caracteres para todos esos caracteres i.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ code to find the minimum
// number of swaps required to
// make the string K periodic
#include <bits/stdc++.h>
using namespace std;
int minFlip(string s, int n,
int k, char a[],
int p)
{
bool allowed[26] = { 0 };
for (int i = 0; i < p; i++) {
// Mark all allowed
// characters as true
allowed[a[i] - 'a'] = true;
}
char freq[k][26];
// Initialize the freq array to 0
for (int i = 0; i < k; i++)
for (int j = 0; j < 26; j++)
freq[i][j] = 0;
for (int i = 0; i < n; i++) {
// Increase the frequency
// of each character
freq[i % k][s[i] - 'a'] += 1;
}
int ans = 0;
// Total number of periods of
// size K in the string
int totalpositions = n / k;
for (int i = 0; i < k; i++) {
int maxfrequency = 0;
for (int j = 0; j < 26; j++) {
// Check if the current character
// is present in allowed
// and whether the current
// frequency is greater than
// all previous frequencies
// for this position
if (freq[i][j] > maxfrequency
and allowed[j] == true)
maxfrequency = freq[i][j];
}
// update the answer by
// subtracting the maxfrequency
// from total positions
// if there exist extra character
// at the end of the string
// apart from the n/k characters
// then add 1.
ans
+= (totalpositions
- maxfrequency
+ ((i % k < n % k)
? 1
: 0));
}
cout << ans << endl;
}
// Driver code
int main()
{
string S = "nihsiakyt";
int n = S.length();
int K = 3;
char A[5]
= { 'n', 'i', 'p', 's', 'q' };
int p = sizeof(A) / sizeof(A[0]);
minFlip(S, n, K, A, p);
return 0;
}
Java
// Java code to find the minimum
// number of swaps required to
// make the String K periodic
import java.util.*;
class GFG{
static void minFlip(String s, int n,
int k, char a[],
int p)
{
boolean allowed[] = new boolean[26];
for(int i = 0; i < p; i++)
{
// Mark all allowed
// characters as true
allowed[a[i] - 'a'] = true;
}
char [][]freq = new char[k][26];
// Initialize the freq array to 0
for(int i = 0; i < k; i++)
for(int j = 0; j < 26; j++)
freq[i][j] = 0;
for(int i = 0; i < n; i++)
{
// Increase the frequency
// of each character
freq[i % k][s.charAt(i) - 'a'] += 1;
}
int ans = 0;
// Total number of periods
// of size K in the String
int totalpositions = n / k;
for(int i = 0; i < k; i++)
{
int maxfrequency = 0;
for(int j = 0; j < 26; j++)
{
// Check if the current character
// is present in allowed
// and whether the current
// frequency is greater than
// all previous frequencies
// for this position
if (freq[i][j] > maxfrequency &&
allowed[j] == true)
maxfrequency = freq[i][j];
}
// Update the answer by
// subtracting the maxfrequency
// from total positions
// if there exist extra character
// at the end of the String
// apart from the n/k characters
// then add 1.
ans += (totalpositions -
maxfrequency +
((i % k < n %
k) ? 1 : 0));
}
System.out.print(ans + "\n");
}
// Driver code
public static void main(String[] args)
{
String S = "nihsiakyt";
int n = S.length();
int K = 3;
char []A = { 'n', 'i', 'p', 's', 'q' };
int p = A.length;
minFlip(S, n, K, A, p);
}
}
// This code is contributed by Amit Katiyar
Python3
# Python3 code to find the minimum
# number of swaps required to
# make the string K periodic
def minFlip(s, n, k, a, p):
allowed = [0] * 26
for i in range(p):
# Mark all allowed
# characters as true
allowed[ord(a[i]) - ord('a')] = True
freq = [[0 for x in range(26)]
for y in range(k)]
# Initialize the freq array to 0
for i in range(k):
for j in range(26):
freq[i][j] = 0
for i in range(n):
# Increase the frequency
# of each character
freq[i % k][ord(s[i]) - ord('a')] += 1
ans = 0
# Total number of periods of
# size K in the string
totalpositions = n // k
for i in range(k):
maxfrequency = 0
for j in range(26):
# Check if the current character
# is present in allowed
# and whether the current
# frequency is greater than
# all previous frequencies
# for this position
if (freq[i][j] > maxfrequency and
allowed[j] == True):
maxfrequency = freq[i][j]
# Update the answer by
# subtracting the maxfrequency
# from total positions
# if there exist extra character
# at the end of the string
# apart from the n/k characters
# then add 1.
ans += (totalpositions - maxfrequency)
if (i % k < n % k):
ans += 1
print(ans)
# Driver code
if __name__ == "__main__":
S = "nihsiakyt"
n = len(S)
K = 3
A = [ 'n', 'i', 'p', 's', 'q' ]
p = len(A)
minFlip(S, n, K, A, p)
# This code is contributed by chitranayal
C#
// C# code to find the minimum
// number of swaps required to
// make the String K periodic
using System;
class GFG{
static void minFlip(String s, int n,
int k, char []a,
int p)
{
bool []allowed = new bool[26];
for(int i = 0; i < p; i++)
{
// Mark all allowed
// characters as true
allowed[a[i] - 'a'] = true;
}
char [,]freq = new char[k, 26];
// Initialize the freq array to 0
for(int i = 0; i < k; i++)
for(int j = 0; j < 26; j++)
freq[i, j] = (char)0;
for(int i = 0; i < n; i++)
{
// Increase the frequency
// of each character
freq[i % k, s[i] - 'a'] += (char)1;
}
int ans = 0;
// Total number of periods
// of size K in the String
int totalpositions = n / k;
for(int i = 0; i < k; i++)
{
int maxfrequency = 0;
for(int j = 0; j < 26; j++)
{
// Check if the current character
// is present in allowed
// and whether the current
// frequency is greater than
// all previous frequencies
// for this position
if (freq[i, j] > maxfrequency &&
allowed[j] == true)
maxfrequency = freq[i, j];
}
// Update the answer by
// subtracting the maxfrequency
// from total positions
// if there exist extra character
// at the end of the String
// apart from the n/k characters
// then add 1.
ans += (totalpositions -
maxfrequency +
((i % k < n %
k) ? 1 : 0));
}
Console.Write(ans + "\n");
}
// Driver code
public static void Main(String[] args)
{
String S = "nihsiakyt";
int n = S.Length;
int K = 3;
char []A = { 'n', 'i', 'p', 's', 'q' };
int p = A.Length;
minFlip(S, n, K, A, p);
}
}
// This code is contributed by Rohit_ranjan
Javascript
<script>
// Javascript code for
// the above approach.
function minFlip(s, n, k, a, p)
{
let allowed = Array.from({length: 26}, (_, i) => 0);
for(let i = 0; i < p; i++)
{
// Mark all allowed
// characters as true
allowed[a[i].charCodeAt() - 'a'.charCodeAt()] = true;
}
let freq = new Array(k);
for (var i = 0; i < freq.length; i++) {
freq[i] = new Array(2);
}
// Initialize the freq array to 0
for(let i = 0; i < k; i++)
for(let j = 0; j < 26; j++)
freq[i][j] = 0;
for(let i = 0; i < n; i++)
{
// Increase the frequency
// of each character
freq[i % k][s[i].charCodeAt() - 'a'.charCodeAt()] += 1;
}
let ans = 0;
// Total number of periods
// of size K in the String
let totalpositions = Math.floor(n / k);
for(let i = 0; i < k; i++)
{
let maxfrequency = 0;
for(let j = 0; j < 26; j++)
{
// Check if the current character
// is present in allowed
// and whether the current
// frequency is greater than
// all previous frequencies
// for this position
if (freq[i][j] > maxfrequency &&
allowed[j] == true)
maxfrequency = freq[i][j];
}
// Update the answer by
// subtracting the maxfrequency
// from total positions
// if there exist extra character
// at the end of the String
// apart from the n/k characters
// then add 1.
ans += (totalpositions -
maxfrequency +
((i % k < n %
k) ? 1 : 0));
}
document.write(ans + "\n");
}
// Driver code
let S = "nihsiakyt";
let n = S.length;
let K = 3;
let A = [ 'n', 'i', 'p', 's', 'q' ];
let p = A.length;
minFlip(S, n, K, A, p);
</script>
6
Publicación traducida automáticamente
Artículo escrito por nishitsharma1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA