Número mínimo de cortes necesarios para pagar el salario de la barra de oro de longitud N

Dada una barra de oro de longitud N con N marcas iguales, la tarea es encontrar el número mínimo de cortes necesarios para pagar el salario en N días , de modo que en cualquier i- ^ésimo día el trabajador tenga i partes de la barra de oro.
Ejemplos: 
 

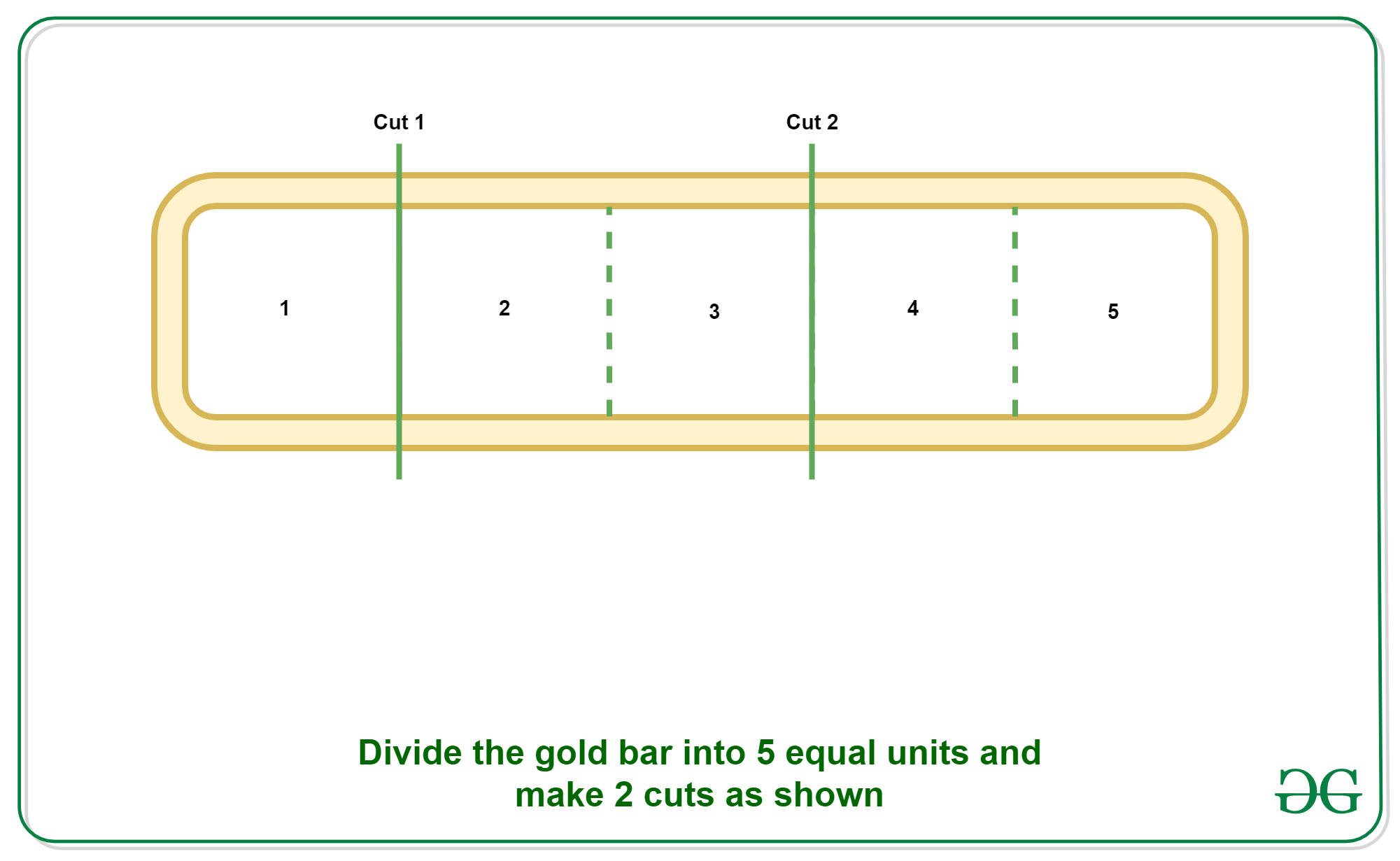
Entrada: N = 5 
Salida: 2 
Explicación: 
Divida la barra de oro de 5 longitudes en 3 partes de longitud 1, 2, 2 haciendo 2 cortes. Entonces el salario para cada día será como: 
Para el Día 1 = 1 (Dé 1 barra de longitud) 
Para el Día 2 = 2 – 1 = 1 (Dé 2 barras de longitud y recupere 1 barra de longitud) 
Para el Día 3 = 1 (Dé 1 barra de longitud) barra) 
Para el Día 4 = 2 – 1 = 1 (Dar 2 barras de longitud y retirar 1 barra de longitud) 
Para el Día 5 = 1 (Dar 1 barra de longitud) 
 

Entrada: N = 15 
Salida: 3 
Explicación: 
Divida la barra de oro de 15 longitudes en 4 partes de longitud 1, 2, 4, 8 haciendo 3 cortes. Entonces el salario para cada día será como: 
Para el Día 1 = 1 (Dé 1 barra de longitud) 
Para el Día 2 = 2 – 1 = 1 (Dé 2 barras de longitud y recupere 1 barra de longitud) 
Para el Día 3 = 1 (Dé 1 barra de longitud) barra) 
Para el día 4 = 4 – 2 – 1 = 1 (dar 4 barras de longitud y quitar 1 y 2 barras de longitud) 
Para el día 5 = 1 (dar 1 barra de longitud) 
Para el día 6 = 2 – 1 = 1 (dar 2 barras) barra de longitud y retirar 1 barra de longitud) 
Para el día 7 = 1 (dar 1 barra de longitud) 
Para el día 8 = 8 – 4 – 2 – 1 = 1 (dar 8 barras de longitud y retirar 1, 2 y 4 barras de longitud) 
Para Día 9 = 1 (Dé 1 barra de longitud) 
Para el día 10 = 2 – 1 = 1 (dar 2 barras de longitud y quitar 1 barra de longitud) 
Para el día 11 = 1 (dar 1 barra de longitud) 
Para el día 12 = 4 – 2 – 1 = 1 (dar 4 barras de longitud y quitar atrás 1 y 2 barra de largo) 
Para el día 13 = 1 (dar 1 barra de largo) 
Para el día 14 = 2 – 1 = 1 (dar 2 barras de largo y retirar 1 barra de largo) 
Para el día 15 = 1 (dar 1 barra de largo) 
 

Planteamiento: 
Como sabemos cualquier número se puede representar con la ayuda de los números en forma de potencias de 2 . Entonces, si cortamos la longitud de la barra de oro en el entero más cercano a log ₂ (N), entonces podemos representar cualquier número hasta N. 
Por ejemplo: cuando N = 15, podemos dividir el número en las partes 1, 2, 4 , 8 y usando estos números podemos representar cualquier número del 1 al 15, como se muestra a continuación: 
 

For 1 - 1
For 2 - 2
For 3 - 2 + 1
For 4 - 4
For 5 - 4 + 1
For 6 - 4 + 2
For 7 - 4 + 2 + 1
For 8 - 8
For 9 - 8 + 1
For 10 - 8 + 2
For 11 - 8 + 2 + 1
For 12 - 8 + 4
For 13 - 8 + 4 + 1
For 14 - 8 + 4 + 2
For 15 - 8 + 4 + 2 + 1

A continuación se muestra la implementación del enfoque anterior.
 

// CPP Implementation to find
// the minimum number of cuts to
// pay the worker.
#include <bits/stdc++.h>
 
using namespace std;
 
// Function to find the minimum
// number of cuts to pay the worker.
int pay(int n)
{
 
    // Nearest Integer to the Log
    // value of the number N
    int cuts = int(log(n)/log(2));
 
    return cuts;
}
 
// Driver code
int main()
{
    int n = 5;
    int cuts = pay(n);
    cout << cuts << endl;
     
    // Cuts Required in the
    // Length of 15
    n = 15;
    cuts = pay(n);
    cout<<(cuts);
     
    return 0;
}
 
// This code is contributed by mohit kumar 29

// JAVA Implementation to find
// the minimum number of cuts to
// pay the worker.
class GFG
{
 
// Function to find the minimum
// number of cuts to pay the worker.
static int pay(int n)
{
 
    // Nearest Integer to the Log
    // value of the number N
    int cuts = (int) (Math.log(n)/Math.log(2));
 
    return cuts;
}
 
// Driver code
public static void main(String[] args)
{
    int n = 5;
    int cuts = pay(n);
    System.out.print(cuts +"\n");
     
    // Cuts Required in the
    // Length of 15
    n = 15;
    cuts = pay(n);
    System.out.print(cuts);
}
}
 
// This code is contributed by 29AjayKumar

# Python Implementation to find
# the minimum number of cuts to
# pay the worker.
 
import math
 
# Function to find the minimum
# number of cuts to pay the worker.
def pay(n):
     
    # Nearest Integer to the Log
    # value of the number N
    cuts = int(math.log(n, 2))
     
    return cuts
     
# Driver Code
if __name__ == "__main__":
    n = 5
    cuts = pay(n)
    print(cuts)
     
    # Cuts Required in the
    # Length of 15
    n = 15
    cuts = pay(n)
    print(cuts)

// C# Implementation to find
// the minimum number of cuts to
// pay the worker.
using System;
 
class GFG
{
 
// Function to find the minimum
// number of cuts to pay the worker.
static int pay(int n)
{
 
    // Nearest int to the Log
    // value of the number N
    int cuts = (int) (Math.Log(n)/Math.Log(2));
 
    return cuts;
}
 
// Driver code
public static void Main(String[] args)
{
    int n = 5;
    int cuts = pay(n);
    Console.Write(cuts +"\n");
     
    // Cuts Required in the
    // Length of 15
    n = 15;
    cuts = pay(n);
    Console.Write(cuts);
}
}
 
// This code is contributed by 29AjayKumar

<script>
 
// JavaScript Implementation to find
// the minimum number of cuts to
// pay the worker.
 
// Function to find the minimum
// number of cuts to pay the worker.
function pay(n)
{
 
    // Nearest Integer to the Log
    // value of the number N
    let cuts = parseInt(Math.log(n)/Math.log(2));
 
    return cuts;
}
 
// Driver code
    let n = 5;
    let cuts = pay(n);
    document.write(cuts + "<br>");
     
    // Cuts Required in the
    // Length of 15
    n = 15;
    cuts = pay(n);
    document.write(cuts + "<br>");
 
</script>

2
3

Complejidad de tiempo: O(1)

Espacio Auxiliar: O(1)