Si un gráfico es un gráfico completo con n vértices, entonces el número total de árboles de expansión es n (n-2) donde n es el número de Nodes en el gráfico. En el gráfico completo, la tarea es igual a contar diferentes árboles etiquetados con n Nodes para los cuales tenemos la fórmula de Cayley .
¿Qué pasa si el gráfico no está completo?
Siga el procedimiento dado:
- PASO 1: Crear array de adyacencia para el gráfico dado.
- PASO 2: Reemplace todos los elementos diagonales con el grado de los Nodes. Por ej. el elemento en la posición (1,1) de la array de adyacencia será reemplazado por el grado del Node 1, el elemento en la posición (2,2) de la array de adyacencia será reemplazado por el grado del Node 2, y así sucesivamente.
- PASO 3: Reemplace todos los 1 no diagonales con -1.
- PASO 4: Calcule el cofactor para cualquier elemento.
- PASO 5: El cofactor que obtienes es el número total de árboles de expansión para ese gráfico.
Considere el siguiente gráfico:
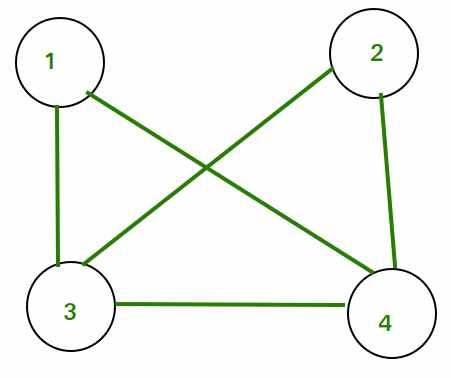
La array de adyacencia para el gráfico anterior será la siguiente:
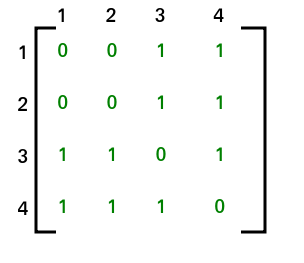
Después de aplicar el PASO 2 y el PASO 3, la array de adyacencia se verá como
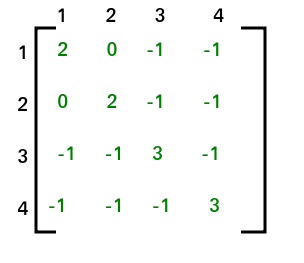
El cofactor para (1, 1) es 8. Por lo tanto, el número total. de spanning tree que se puede formar es 8.
NOTA: El cofactor para todos los elementos será el mismo. Por lo tanto, podemos calcular el cofactor para cualquier elemento de la array. Este método también se conoce como Teorema de Kirchhoff . También se puede aplicar a gráficos completos.
Este artículo es una contribución de Kapil Khandelwal . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo y enviarlo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA