numpy.polyint(p, m) : Evalúa la antiderivada de un polinomio con el orden especificado.
m antiderivada ‘P’ del polinomio ‘p’ satisface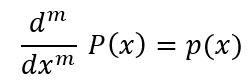
Parámetros:
p: [array_like o poly1D] los coeficientes polinómicos se dan en orden decreciente de potencias. Si el segundo parámetro (raíz) se establece en Verdadero, los valores de array son las raíces de la ecuación polinomial. Por ejemplo, poli1d(3, 2, 6) = 3x 2 + 2x + 6
m : [int, opcional] Orden de la antiderivada. El valor predeterminado es 1.Retorno: Antiderivada del polinomio.
Código #1:
# Python code explaining
# numpy.polyint()
# importing libraries
import numpy as np
# Constructing polynomial
p1 = np.poly1d([1, 2])
p2 = np.poly1d([4, 9, 5, 4])
print ("P1 : ", p1)
print ("\n p2 : \n", p2)
# Solve for x = 2
print ("\n\np1 at x = 2 : ", p1(2))
print ("p2 at x = 2 : ", p2(2))
a = np.polyint(p1, 1)
b = np.polyint(p2, 1)
print ("\n\nUsing polyint")
print ("p1 anti-derivative of order = 1 : \n", a)
print ("p2 anti-derivative of order = 1 : \n", b)
a = np.polyint(p1, 2)
b = np.polyint(p2, 2)
print ("\n\nUsing polyint")
print ("p1 anti-derivative of order = 2 : \n", a)
print ("p2 anti-derivative of order = 2 : \n", b)
Producción :
P1 :
1 x + 2
p2 :
3 2
4 x + 9 x + 5 x + 4
p1 at x = 2 : 4
p2 at x = 2 : 82
Using polyint
p1 anti-derivative of order = 1 :
2
0.5 x + 2 x
p2 anti-derivative of order = 1 :
4 3 2
1 x + 3 x + 2.5 x + 4 x
Código #2:
# Python code explaining
# numpy.polyint()
# importing libraries
import numpy as np
# Constructing polynomial
p1 = np.poly1d([1, 2])
p2 = np.poly1d([4, 9, 5, 4])
a = np.polyint(p1, 2)
b = np.polyint(p2, 2)
print ("\n\nUsing polyint")
print ("p1 anti-derivative of order = 2 : \n", a)
print ("p2 anti-derivative of order = 2 : \n", b)
Producción :
Using polyint
p1 anti-derivative of order = 2 :
3 2
0.1667 x + 1 x
p2 anti-derivative of order = 2 :
5 4 3 2
0.2 x + 0.75 x + 0.8333 x + 2 x
Publicación traducida automáticamente
Artículo escrito por Mohit Gupta_OMG 🙂 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA