Requisito previo: crear un gráfico no dirigido .
Las operaciones gráficas básicas son las siguientes:
Obtener subgrafo de un grafo:
Dado un gráfico y un subconjunto de su conjunto de Nodes, podemos crear un subgráfico seleccionando estos Nodes y todos los bordes entre ellos como estaban presentes en el gráfico original. El siguiente código ilustrará claramente esta operación.
import networkx as nx
import matplotlib.pyplot as plt
G = nx.Graph()
plt.figure(figsize =(9, 12))
G.add_edges_from([(1, 2), (1, 3), (2, 3), (2, 4), (2, 5), (3, 4),
(4, 5), (4, 6), (5, 7), (5, 8), (7, 8)])
# original Graph created
plt.subplot(211)
print("The original Graph:")
nx.draw_networkx(G)
El gráfico original:
H = G.subgraph([1, 2, 3, 4])
# [1, 2, 3, 4] is the subset of
# the original set of nodes
plt.subplot(212)
print("The Subgraph:")
nx.draw_networkx(H)
El Subgrafo: El Grafico 
G original tiene Nodes del 1 al 8. Hemos seleccionado los Nodes 1, 2, 3 y 4 y creamos un Subgrafo H que tiene 5 aristas que estaban presentes entre ellos en el grafo G original.
Unión de dos Grafos:
Dados dos gráficos G y H, la unión de los 2 gráficos crea un único gráfico que puede tener múltiples componentes conectados. Pero debemos tener en cuenta que el conjunto de Nodes de G y H debe ser disjunto, en otras palabras, los dos gráficos no deben tener ningún Node en común.
import networkx as nx import matplotlib.pyplot as plt G = nx.Graph() plt.figure(figsize =(9, 12)) G.add_edges_from([(1, 2), (1, 3), (2, 3), (2, 4), (2, 5), (3, 4), (4, 5), (4, 6), (5, 7), (5, 8), (7, 8)]) # First Graph created plt.subplot(311) nx.draw_networkx(G) H = nx.Graph() H.add_edges_from([(13, 14), (13, 15), (13, 9), (14, 15), (15, 10), (9, 10)]) # Second Graph created plt.subplot(312) nx.draw_networkx(H) I = nx.union(G, H) plt.subplot(313) nx.draw_networkx(I)

El gráfico recién formado I es la unión de los gráficos g y H. Si tenemos Nodes comunes entre dos gráficos y todavía queremos obtener su unión, entonces usaremos otra función llamadadisjoint_set()
I = nx.disjoint_set(G, H)
Esto cambiará el nombre de los Nodes comunes y formará un gráfico similar.
Producto cartesiano de dos gráficos:
Dados dos gráficos, G y H, el producto cartesiano crea un nuevo Gráfico, I = G*H. El conjunto de Nodes de I es el producto cartesiano de conjuntos de Nodes de G y H, es decir, V(I) = V(G)*V(H).
Una arista (( ![]() ), (
), ( ![]() )) existe si y solo si:
)) existe si y solo si:
- i=k y
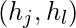 existe como una arista en H
existe como una arista en H - j=l y
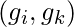 existe como una arista en G
existe como una arista en G
import networkx as nx import matplotlib.pyplot as plt G = nx.Graph() plt.figure(figsize =(9, 18)) G.add_edges_from([(1, 2), (2, 3)]) # First Graph created plt.subplot(311) nx.draw_networkx(G) H = nx.Graph() H.add_edges_from([(6, 7)]) # Second Graph created plt.subplot(312) nx.draw_networkx(H) I = nx.cartesian_product(G, H) plt.subplot(313) nx.draw_networkx(I)

This representation clearly shows how the product of the first 2 graphs result in the third graph.
Composición de dos gráficos:
Dados dos gráficos G y H, si no tienen Nodes comunes, la composición de los dos dará como resultado un solo gráfico con 2 componentes conectados (suponiendo que G y H son gráficos conectados). Este es el mismo resultado que obtendremos si usamos nx.union(G, H)o nx.disjoint_union(G, H).
Pero si G y H tienen Nodes comunes, la composición resultante de estos dos gráficos dará como resultado un único gráfico conexo de tal manera que G y H son subgráficos del nuevo gráfico.
import networkx as nx import matplotlib.pyplot as plt G = nx.Graph() plt.figure(figsize =(9, 15)) G.add_edges_from([(1, 2), (1, 3), (2, 3), (2, 4)]) # First Graph created plt.subplot(311) nx.draw_networkx(G) H = nx.Graph() H.add_edges_from([(3, 7), (7, 4), (3, 4)]) # Second Graph created plt.subplot(312) nx.draw_networkx(H) I = nx.compose(G, H) plt.subplot(313) nx.draw_networkx(I)

Los diagramas visualizan claramente cómo se componen los dos primeros gráficos para formar el tercer gráfico.
Complemento de un gráfico:
Dado un grafo G, el complemento de G (digamos, H) tiene todos los Nodes de G. Tiene todas las aristas posibles que G no tiene. Sean V y E el conjunto de Nodes y aristas de G, entonces H tiene {(|V|*(|V|-1))/2 - |E|} número de aristas. Por tanto, el complemento de un Grafo completo no tendrá aristas.
import networkx as nx import matplotlib.pyplot as plt G = nx.Graph() plt.figure(figsize =(9, 16)) G.add_edges_from([(1, 2), (1, 3), (2, 3), (2, 4)]) # Original Graph created plt.subplot(211) nx.draw_networkx(G) H = nx.complement(G) plt.subplot(212) nx.draw_networkx(H)

Convertir a Dirigido:
Dado un gráfico G no dirigido, esta función Networkx lo convertirá en un gráfico dirigido reemplazando sus bordes con bordes dirigidos de 2 vías.
import networkx as nx import matplotlib.pyplot as plt G = nx.Graph() plt.figure(figsize =(9, 16)) G.add_edges_from([(1, 2), (1, 3), (2, 3), (2, 4)]) # Original Undirected Graph created plt.subplot(211) nx.draw_networkx(G) H = nx.to_directed(G) plt.subplot(212) nx.draw_networkx(H)

Convertir a no dirigido:
Dado un gráfico dirigido G, esta función Networkx lo convertirá en un gráfico no dirigido al convertir todos sus bordes dirigidos en bordes no dirigidos. Si existen dos bordes entre un par de Nodes con diferentes atributos (pesos, color, etc.), solo se crea un borde con una elección arbitraria de qué datos de borde usar.
import networkx as nx import matplotlib.pyplot as plt G = nx.DiGraph() plt.figure(figsize =(9, 16)) G.add_edges_from([(1, 2), (1, 3), (2, 4)]) # Original Directed Graph created plt.subplot(211) nx.draw_networkx(G) H = nx.to_undirected(G) plt.subplot(212) nx.draw_networkx(H)

Ahora, discutiremos los diversos gráficos especiales que ofrece el módulo Networkx.
Gráfico de Petersen: El gráfico de Petersen es un gráfico no dirigido con 10 vértices y 15 aristas. Es un pequeño gráfico que sirve como ejemplo y contraejemplo útil para muchos problemas de teoría de grafos.
import networkx as nx import matplotlib.pyplot as plt plt.figure(figsize =(9, 100)) # Peterson Graph plt.subplot(12, 1, 1) G = nx.petersen_graph() nx.draw_networkx(G)

Gráfico Tutte: El gráfico Tutte es un gráfico regular de 3 con 46 vértices y 69 aristas. El gráfico de Tutte es un gráfico poliédrico cúbico , pero no hamiltoniano . Por tanto, es un contraejemplo a la conjetura de Tait. que todo poliedro regular de 3 tiene un ciclo hamiltoniano.
# Tutte Graph plt.subplot(12, 1, 2) G = nx.tutte_graph() nx.draw_networkx(G)

Gráfico de laberinto de Sedgewick: el algoritmo de laberinto de Sedgewick se utiliza para generar laberintos grandes. La función Networkx perteneciente a este método devuelve un pequeño laberinto con un ciclo.
# Sedgewick Maze Graph plt.subplot(12, 1, 3) G = nx.sedgewick_maze_graph() nx.draw_networkx(G)

Gráfico tetraédrico: devuelve un gráfico completo con cuatro Nodes que tienen forma de tetraedro.
# Tetrahedral Graph plt.subplot(12, 1, 4) G = nx.tetrahedral_graph() nx.draw_networkx(G)

Gráfico completo: devuelve un gráfico completo con un número determinado de aristas.
# Complete Graph with 5 nodes plt.subplot(12, 1, 5) G = nx.complete_graph(6) nx.draw_networkx(G)

Gráfico bipartito completo: dados dos números n y m, devuelve un gráfico con dos conjuntos de n y m Nodes de tal manera que un Node de un conjunto está conectado a todos los Nodes del otro conjunto pero sin Node propio establecer. Este tipo de Gráfico se conoce como Bipartito .
# Complete Bipartite Graph with 5 and 3 nodes plt.subplot(12, 1, 6) G = nx.complete_bipartite_graph(5, 3) nx.draw_networkx(G)

Barbell Graph: dados dos parámetros n y m, devuelve un gráfico con dos camarillas de n Nodes que están conectados a través de m Nodes en el medio.
# Barbell Graph with clique of 4 and bridging of 2 nodes plt.subplot(12, 1, 7) G = nx.barbell_graph(4, 2) nx.draw_networkx(G)

Lollipop Graph: dados dos parámetros n y m, devuelve un gráfico con una camarilla de n vértices conectados a una ruta de m Nodes.
# Lollipop Graph with clique of 5 and path of 2 nodes plt.subplot(12, 1, 8) G = nx.lollipop_graph(5, 2) nx.draw_networkx(G)

Erdos Renyi Graph: dados dos parámetros n y p, devuelve un gráfico con n Nodes con una probabilidad de p para seleccionar cada borde. Para más detalles, consulte este artículo.
# Erdos Renyi Graph with 20 nodes and probability of 0.25 plt.subplot(12, 1, 9) G = nx.erdos_renyi_graph(20, 0.25) nx.draw_networkx(G)

Gráfico de Watts Strogatz: dados tres parámetros n, k y p, devuelve una red de mundo pequeño de n Nodes, cada uno de los cuales está conectado a k vecinos más cercanos con una probabilidad de p de volver a cablear cada borde.
# Watts Strogatz Graph with 20 nodes, # 4 neighbours and probability of 0.2 plt.subplot(12, 1, 10) G = nx.watts_strogatz_graph(20, 4, 0.2) nx.draw_networkx(G)

Barabasi Albert Graph: dados dos parámetros n y m, devuelve un gráfico adjunto preferencial de Barabasi Albert con n Nodes y m cantidad de bordes para adjuntar desde un nuevo Node a los Nodes existentes.
# Barabasi Albert Graph with 20 nodes and 3 attaching nodes plt.subplot(12, 1, 11) G = nx.barabasi_albert_graph(20, 3) nx.draw_networkx(G)

Gráfico de langosta aleatorio: dados tres parámetros n, p1 y p2, devuelve un gráfico de langosta. Una langosta es un árbol que se reduce a una oruga al podar todos los nudos de las hojas. Una oruga es un árbol que se reduce a un gráfico de ruta al podar todos los Nodes de hoja. El gráfico tiene n Nodes en la columna vertebral, p1 probabilidad de agregar un borde a la columna vertebral, p2 probabilidad de agregar un borde un nivel más allá de la columna vertebral.
# Random Lobster Graph with 30 base # nodes and probabilites of 0.8 plt.subplot(12, 1, 12) G = nx.random_lobster(30, 0.8, 0.8) nx.draw_networkx(G)

Publicación traducida automáticamente
Artículo escrito por ArijitGayen y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA