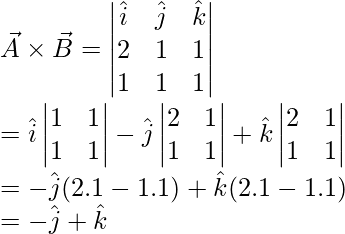Operaciones vectoriales – Barcelona Geeks

En física, existen principalmente dos tipos de cantidades: vectoriales y escalares. Los vectores son cantidades que tienen dirección y magnitud asociadas, mientras que los escalares son las cantidades que tienen la única magnitud asociada. Las cantidades escalares se pueden tratar usando reglas algebraicas simples, pero este no es el caso de las cantidades vectoriales, no se pueden tratar de la misma manera. Por lo tanto, es fundamental saber qué tipo y cuántas operaciones diferentes se pueden realizar sobre estas cantidades. Veamos algunas de estas operaciones en detalle.

Operaciones Matemáticas en Vectores

Dado que los vectores contienen direcciones, estas cantidades deben tratarse de manera que se tengan en cuenta sus direcciones. Las reglas básicas del álgebra no se aplican en general a los vectores, por ejemplo: una simple suma de las magnitudes de los dos vectores dará una respuesta incorrecta en la mayoría de los casos. La siguiente lista es la lista de algunas de las operaciones comunes que se realizan en los vectores en el campo de la física:

Suma/Resta de dos vectores.
Multiplicación de vectores con escalares.
Producto de dos vectores:
- Producto escalar
- Producto cruzado

Adición de vectores

Los vectores no se pueden sumar por las reglas algebraicas habituales. Al sumar dos vectores, se debe tener en cuenta la magnitud y la dirección de los vectores. La ley del triángulo se usa para sumar dos vectores, el siguiente diagrama muestra dos vectores «a» y «b» y la resultante calculada después de su suma. La suma de vectores sigue la propiedad conmutativa, esto significa que el vector resultante es independiente del orden en que se suman los dos vectores.

$\vec{a} + \vec{b} = \vec{c}$

$\vec{a} + \vec{b} = \vec{b} + \vec{a}$ ⇢ (Propiedad Conmutativa)

Ley del Triángulo de la Suma de Vectores

Considere los vectores dados en la figura anterior. La línea PQ representa el vector “p”, y QR representa el vector “q”. La línea QR representa el vector resultante. La dirección de AC es de A a C.

La línea AC representa,

$\vec{p} + \vec{q}$

La magnitud del vector resultante viene dada por,

$\sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}$

El $\theta$ representa el ángulo entre los dos vectores. Sea \phi el ángulo que forma el vector resultante con el vector p.

$tan(\phi) = \frac{qsin(\theta)}{p + qcos(\theta)}$

Multiplicación de Vectores con Escalar

Multiplicar un vector a con un escalar constante k da un vector cuya dirección es la misma pero la magnitud cambia por un factor de k. La figura muestra el vector antes y después de multiplicarlo por la constante k. En términos matemáticos, esto se puede reescribir como,

$|k\vec{v}| = k|\vec{v}|$

si k > 1, la magnitud del vector aumenta mientras que decrece cuando k < 1.

Producto de Vectores

Los vectores se pueden multiplicar entre sí pero no se pueden dividir. En el caso de la multiplicación, existen básicamente dos tipos de multiplicación: escalar y vectorial. La multiplicación escalar (también conocida como producto escalar) es un tipo de multiplicación que da como resultado una cantidad escalar. La multiplicación vectorial (también conocida como producto cruzado) es un tipo de multiplicación que da como resultado una cantidad vectorial. Los productos vectoriales se utilizan para definir otras cantidades vectoriales derivadas.

Producto escalar

Considere dos vectores y . El producto escalar de estos dos vectores está definido por la ecuación, $\vec{A}$ $\vec{B}$

$\vec{A}.\vec{B} = |\vec{A}||\vec{B}|cos(\theta)$

Aquí,

Considere dos vectores \vec{A} y \vec{B} . El producto vectorial de estos dos vectores se denota por $\vec{A} \times \vec{B}$ . La dirección de este vector es perpendicular a ambos vectores. La magnitud de este vector está dada por,

$|\vec{A} \times \vec{B}| = |\vec{A}||\vec{B}|sin(\theta)$

Aquí,

$\vec{A} \times \vec{B} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{vmatrix} \\$

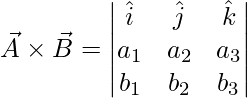
Problemas de muestra

Pregunta 1: Un vector viene dado por, v = 2i + j. Encuentre la magnitud del vector cuando se escala por una constante de 0.4.

Responder:

para un vector, v = ai + bj

|v| = $\sqrt{a^2 + b^2}$

0.4|v| = |0.4v|

a = 2, b = 1

|0.4v|

⇒ |0.4(2i+j)|

⇒ |0.8i + 0.4j|

|v| = $\sqrt{0.8^2 + 0.4^2}$

⇒ |v| = $\sqrt{0.64 + 0.16}$

⇒ |v| = √0.8

Pregunta 2: Dos vectores con magnitud 5 y 10. Estos vectores tienen un ángulo de 60° entre ellos. Encuentre la magnitud de los vectores resultantes.

Responder:

Sean los dos vectores dados por p y q. Entonces el vector resultante “r” está dado por,

$|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}$

|p| = 5, |q| = 10 y $\theta = 60^o$

$|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}$

⇒ $|r| = \sqrt{|5|^2 + |10|^2 + 2|5||10|cos(60)}$

⇒ $|r| = \sqrt{|5|^2 + |10|^2 + (10)(5)}$

⇒ $|r| = \sqrt{25 + 100 + 50}$

⇒ $|r| = \sqrt{175}$

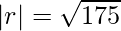
Pregunta 3: Dos vectores con magnitud 4 y 4. Estos vectores tienen un ángulo de 60° entre ellos. Encuentre la magnitud de los vectores resultantes y el ángulo formado por el vector resultante.

Responder:

Sean los dos vectores dados por p y q. Entonces el vector resultante “r” está dado por,

$|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}$

|p| = 4, |q| = 4 y $\theta = 60^o$

$|r| = \sqrt{|p|^2 + |q|^2 + 2|p||q|cos(\theta)}$

⇒ $|r| = \sqrt{|4|^2 + |4|^2 + 2|4||4|cos(60)}$

⇒ $|r| = \sqrt{16 + 16 + 2|4||4|cos(60)}$

⇒ $|r| = \sqrt{48}$

⇒ |r| = 4√3

ángulo formado por la resultante,

$tan(\phi) = \frac{4sin(60)}{4 + 4cos(60)}$

⇒ $tan(\phi) = \frac{2\sqrt{2}}{4 + 2}$

⇒ $tan(\phi) = \frac{\sqrt{2}}{3}$

⇒ $\phi = tan{-1}(\frac{\sqrt{2}}{3})$

Pregunta 4: Dos vectores están dados por, a = 2i + j + k y b = i + j + k. Encuentra el producto escalar de estos dos vectores.

Responder:

Dado:

a = 2i + j + k

segundo = yo + j + k

abdominales

⇒ (2i + j + k ).(i + j + k)

⇒ 2,1 + 1,1 + 1,1

⇒ 4

Pregunta 5: Dos vectores están dados por, a = 2i + j + k y b = i + j + k. Encuentra el producto cruz de estos dos vectores.

Responder:

Dado:

a = 2i + j + k

segundo = yo + j + k

$\vec{A} \times \vec{B} = \begin{vmatrix} \hat{i} & \hat{j} & \hat{k} \\ 2 & 1 & 1 \\ 1 & 1 & 1 \end{vmatrix} \\ = \hat{i}\begin{vmatrix} 1 & 1 \\ 1 & 1 \end{vmatrix} - \hat{j}\begin{vmatrix} 2 & 1 \\ 1 & 1 \end{vmatrix} + \hat{k}\begin{vmatrix} 2 & 1 \\ 1 & 1 \end{vmatrix} \\ = -\hat{j}(2.1 - 1.1) + \hat{k}(2.1 - 1.1) \\ = -\hat{j} + \hat{k}$

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Operaciones Matemáticas en Vectores

Adición de vectores

Ley del Triángulo de la Suma de Vectores

Multiplicación de Vectores con Escalar

Producto de Vectores

Problemas de muestra

Deja una respuesta Cancelar la respuesta