Los operadores en Julia son los símbolos matemáticos que se utilizan para realizar operaciones en variables y valores. Estos símbolos se utilizan para realizar cálculos aritméticos y lógicos. Las variables sobre las que los operadores realizan operaciones se denominan operandos . En otras palabras, podemos decir que un operador opera los operandos.
Por ejemplo, considere la siguiente declaración:
c = a + b;
Aquí, ‘+’ es el operador conocido como operador de suma y ‘a’ y ‘b’ son operandos. El operador de suma le dice al compilador que agregue los dos operandos ‘a’ y ‘b’.
Tipos de Operadores
Los operadores en Julia son de seis tipos:
- Operadores aritméticos
- Operadores bit a bit
- Operadores logicos
- Operadores de Asignación
- Operadores ‘punto’ vectorizados
- Operadores relacionales
Operador aritmético
Los operadores aritméticos se utilizan para realizar operaciones aritméticas/matemáticas en operandos. Estos operadores incluyen el proceso de suma, resta, multiplicación, división, etc. Ejemplos: (+, -, *, /, %, +x, -x).
Los operadores aritméticos son de dos tipos:
- Operadores unarios: Los operadores que operan o trabajan con un solo operando son operadores unarios. Por ejemplo: (+x, -x), es decir, unario más y unario menos.
- Operadores binarios: Los operadores que operan o trabajan con dos operandos son operadores binarios. Por ejemplo: (+, –, *, /)
| Operador | Descripción | Sintaxis |
|---|---|---|
| +(más unario) | Más unario: operación de identidad | +x |
| -(menos unario) | Menos unario: realiza la negación en el operando | -X |
| + | Más binario: suma dos operandos | x + y |
| – | Menos binario: resta dos operandos | x – y |
| * | Multiplicación (veces): multiplica dos operandos | x * y |
| / | División (flotante): divide el primer operando por el segundo y devuelve el valor flotante | x / y |
| ÷ | División (Entero): divide el primer operando por el segundo y devuelve un valor entero | x ÷ y |
| \ | División (Inversa): divide el segundo operando por el primero (y/x) | x \ y |
| ^ | Potencia: Eleva x a la yésima potencia | x ^ y |
| % | Módulo: devuelve el resto cuando el primer operando se divide por el segundo | x % y |
| ! | Negación: cambia el valor booleano, es decir, de verdadero a falso y viceversa | x % y |
# Examples of Arithmetic Operator
a = 9
b = 4
println("a = ", a)
println("b = ", b)
# Addition of numbers
add = a + b
println("Binary Addition: ", add)
# Subtraction of numbers
sub = a - b
println("Binary Subtraction: ", sub)
# Multiplication of number
mul = a * b
println("Binary Multiplication: ", mul)
# Division(float) of number
div1 = a / b
println("Binary Division: ", div1)
# Division(Integer) of number
div2 = a ÷ b
println("Integer Division: ", div2)
# Division(floor) of number
div3 = a \ b
println("Inverse Division: ", div3)
# Power of number
pow = a ^ b
println("Power Operation: ", pow)
# Modulo of both number
mod = a % b
println("Modular Division: ", mod)
Producción:
a = 9 b = 4 Binary Addition: 13 Binary Subtraction: 5 Binary Multiplication: 36 Binary Division: 2.25 Integer Division: 2 Inverse Division: 0.4444444444444444 Power Operation: 6561 Modular Division: 1
Operador bit a bit
Los operadores bit a bit se utilizan para realizar la manipulación de bits individuales de un número. Se pueden utilizar con cualquiera de los tipos enteros. Ejemplos: (~, &, |, >>, <<, etc.)
| Operador | Descripción | Sintaxis |
|---|---|---|
| ~ | bit a bit NO | ~ x |
| & | Y bit a bit | x e y |
| | | O bit a bit | x | y |
| ⊻ | XOR bit a bit | x ⊻ y |
| >>> | Desplazamiento lógico a la derecha | x >>> y |
| >> | Desplazamiento a la derecha bit a bit | x >> y |
| << | Desplazamiento a la izquierda bit a bit/lógico | x << y |
# Examples of Bitwise operators a = 48 b = 67 # Bitwise NOT operation println(~a) # Bitwise AND operation println(a & b) # Bitwise OR operation println(a | b) # Bitwise XOR operation println(a ? b) # Logical right shift operation println(a >>> 2) # Bitwise right shift operation println(a >> 2) # Bitwise left shift operation println(a << 2)
Producción:
-49 0 115 115 12 12 192
Operador lógico
Los operadores lógicos se utilizan para combinar dos o más condiciones/restricciones o para complementar la evaluación de la condición original en consideración. El resultado de la operación de un operador lógico es un valor booleano, ya sea verdadero o falso. Por ejemplo, el operador AND lógico representado como ‘&&’ en Julia devuelve verdadero cuando se cumplen las dos condiciones consideradas. De lo contrario, devuelve falso. Por lo tanto, a && b devuelve verdadero cuando tanto a como b son verdaderos (es decir, distintos de cero).
| Operador | Descripción | Sintaxis |
|---|---|---|
| && | Y lógico: Verdadero si ambos operandos son verdaderos | x & & y |
| || | OR lógico: Verdadero si cualquiera de los operandos es verdadero | x || y |
| ! | NOT lógico: verdadero si el operando es falso | !X |
# Examples of Logical Operator a = true b = false # Print if a and b both are False println(a && b) # Print if a or b is True println(a || b) # Print if not a is False println(! a)
Producción:
false true false
Operador de asignación
Los operadores de asignación se utilizan para asignar valor a una variable. El operando del lado izquierdo del operador de asignación es una variable y el operando del lado derecho del operador de asignación es un valor. El valor del lado derecho debe ser del mismo tipo de datos que la variable del lado izquierdo; de lo contrario, el compilador generará un error.
| Operador | Descripción | Sintaxis |
|---|---|---|
| = | Asigne el valor del lado derecho de la expresión al operando del lado izquierdo | x = y + z |
| += | Añadir Y: Añadir el operando del lado derecho con el operando del lado izquierdo y luego asignarlo al operando de la izquierda | a += ba = a + b |
| -= | Restar Y: restar el operando derecho del operando izquierdo y luego asignarlo al operando izquierdo | a -= ba = a – b |
| *= | Multiplicar AND: Multiplicar el operando derecho con el operando izquierdo y luego asignarlo al operando izquierdo | a * = ba = a * b |
| /= | Divide AND: divide el operando izquierdo con el operando derecho y luego asigna el operando izquierdo | a /= ba = a / b |
| \= | Dividir inversamente Y: dividir el operando derecho con el operando izquierdo y luego asignarlo al operando izquierdo | un \= ba = un \ segundo |
| ÷= | Integer Divide AND: Divide el operando izquierdo con el operando derecho y luego asigna el operando izquierdo | a ÷ = ba = a ÷ b |
| %= | Módulo Y: toma el módulo usando los operandos izquierdo y derecho y asigna el resultado al operando izquierdo | a %= ba = a % b |
| ^= | Exponente Y: Calcule el valor del exponente (elevar la potencia) usando operandos y asigne el valor al operando izquierdo | un ^= ba = un ^ segundo |
| &= | Realiza AND bit a bit en operandos y asigna valor al operando izquierdo | a &= ba = a & b |
| |= | Realiza OR bit a bit en operandos y asigna valor al operando izquierdo | un |= ba = un | b |
| ⊻= | Realiza bitwise xOR en operandos y asigna valor al operando izquierdo | un ⊻= segundo = un ⊻ segundo |
| >>>= | Realiza el desplazamiento lógico a la derecha en los operandos y asigna valor al operando izquierdo | a>>>=ba=a>>>b |
| >>= | Realiza el desplazamiento a la derecha bit a bit en los operandos y asigna valor al operando izquierdo | a >>= ba = a >> b |
| <<= | Realiza el desplazamiento a la izquierda bit a bit en los operandos y asigna valor al operando izquierdo | a <<= ba = a << b |
# Examples of Assignment Operator
a = 9
b = 4
println("a = ", a)
println("b = ", b)
# Addition of numbers
a += b
println("Binary Addition: ", a)
# Subtraction of numbers
a -= b
println("Binary Subtraction: ", a)
# Multiplication of number
a *= b
println("Binary Multiplication: ", a)
# Division(float) of number
a /= b
println("Binary Division: ", a)
# Division(Integer) of number
a ÷= b
println("Integer Division: ", a)
# Division(floor) of number
a \= b
println("Inverse Division: ", a)
# Power of number
a ^= b
println("Power Operation: ", a)
# Modulo of both number
a %= b
println("Modular Division: ", a)
Producción
a = 9 b = 4 Binary Addition: 13 Binary Subtraction: 9 Binary Multiplication: 36 Binary Division: 9.0 Integer Division: 2.0 Inverse Division: 2.0 Power Operation: 16.0 Modular Division: 0.0
Operador ‘punto’ vectorizado
Un operador ‘punto’ (.) se usa para realizar una operación binaria con la que se usa en toda la array, elemento por elemento, uno por uno. Por ejemplo, un operador de potencia (^) si se aplica en una array como [4, 5, 6, 7] ^ 2, dará como resultado un error, porque no es posible realizar el ‘cuadrado’ de una array. Por lo tanto, se utiliza el operador ‘punto’. Cuando se usa con la operación binaria como .^ , realizará la operación en cada elemento de la array. Por ejemplo, [4, 5, 6, 7] ^ 2 resultará en [4^2, 5^2, 6^2, 7^2].
De manera similar, este operador de punto se puede usar con otros operadores binarios como .=, .+, .-, etc.
Ejemplo:
# Julia program to illustrate # use of 'dot' operator # Creating array A = [4, 5, 6, 7] # Performing exponent binary operation A = A ^ 2 # Performing exponent using 'dot' operation A = A .^ 2 println(A)
El código anterior generará un error cuando el exponente se realice sin un operador de ‘punto’ . Esto se debe a que el exponente no se puede realizar en la array de elementos.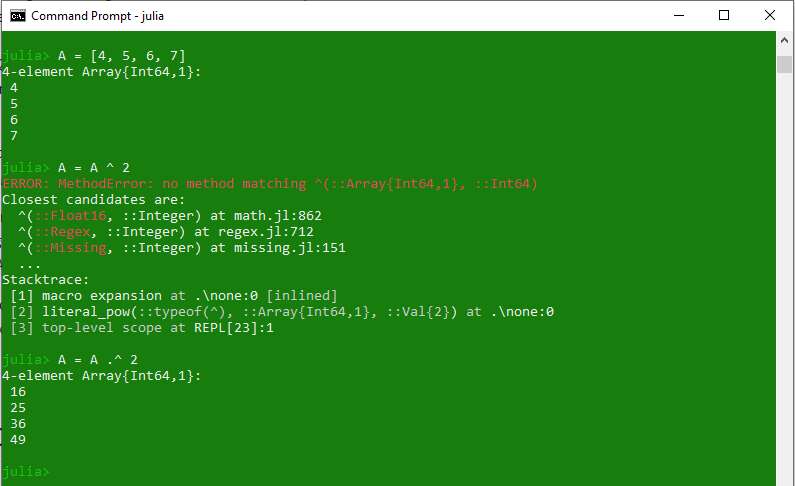
Operador relacional
Estos operadores se utilizan para verificar relaciones como igualdad, mayor que, menor que. Devuelven un resultado booleano después de la comparación y se usan ampliamente en declaraciones de bucle, así como en declaraciones condicionales if-else.
| Operador | Descripción | Sintaxis |
|---|---|---|
| > | Mayor que: Verdadero si el operando izquierdo es mayor que el derecho | x > y |
| < | Menor que: Verdadero si el operando izquierdo es menor que el derecho | x < y |
| == | Igual a: Verdadero si ambos operandos son iguales | x == y |
| !=, ≠ | No es igual a: verdadero si los operandos no son iguales | x != y o x ≠ y |
| >=, ≥ | Mayor o igual que: Verdadero si el operando izquierdo es mayor o igual que el derecho | x >= y o x ≥ y |
| <=, ≤ | Menor o igual que: Verdadero si el operando izquierdo es menor o igual que el derecho | x <= y o x ≤ y |
Ejemplo:
# Examples of Relational Operators a = 13 b = 33 # a > b is False println(a > b) # a < b is True println(a < b) # a == b is False println(a == b) # a != b is True println(a != b) # a >= b is False println(a >= b) # a <= b is True println(a <= b)
Producción:
false true false true false true