Optimización de consultas en álgebra relacional – Part 1

Consulta: Una consulta es una solicitud de información de una base de datos.

Planes de consulta: un plan de consulta (o plan de ejecución de consulta) es un conjunto ordenado de pasos que se utilizan para acceder a los datos en un sistema de administración de base de datos relacional SQL.

Optimización de consultas: una sola consulta puede ejecutarse a través de diferentes algoritmos o reescribirse en diferentes formas y estructuras. Por lo tanto, la cuestión de la optimización de consultas entra en escena: ¿cuál de estas formas o vías es la más óptima? El optimizador de consultas intenta determinar la forma más eficaz de ejecutar una consulta determinada considerando los posibles planes de consulta.

Importancia: el objetivo de la optimización de consultas es reducir los recursos del sistema necesarios para completar una consulta y, en última instancia, proporcionar al usuario el conjunto de resultados correcto más rápido.

En primer lugar, proporciona al usuario resultados más rápidos, lo que hace que la aplicación parezca más rápida para el usuario.
En segundo lugar, permite que el sistema atienda más consultas en la misma cantidad de tiempo, porque cada solicitud lleva menos tiempo que las consultas no optimizadas.
En tercer lugar, la optimización de consultas finalmente reduce la cantidad de desgaste del hardware (por ejemplo, unidades de disco) y permite que el servidor funcione de manera más eficiente (por ejemplo, menor consumo de energía, menos uso de memoria).

En términos generales, hay dos formas en que se puede optimizar una consulta:

Analice y transforme expresiones relacionales equivalentes: intente minimizar los recuentos de tuplas y columnas de los procesos de consulta intermedios y finales (discutidos aquí).
Uso de diferentes algoritmos para cada operación: estos algoritmos subyacentes determinan cómo se accede a las tuplas desde las estructuras de datos en las que están almacenadas, la indexación, el hash, la recuperación de datos y, por lo tanto, influyen en la cantidad de accesos al disco y al bloque (discutido en el procesamiento de consultas).

Analizar y transformar expresiones relacionales equivalentes.
Aquí, hablaremos sobre la generación de expresiones mínimas equivalentes. Para analizar la expresión equivalente, se enumeran un conjunto de reglas de equivalencia. Estos generan expresiones equivalentes para una consulta escrita en álgebra relacional. Para optimizar una consulta, debemos convertir la consulta en su forma equivalente siempre que se cumpla una regla de equivalencia.

Las operaciones de selección conjuntiva se pueden escribir como una secuencia de selecciones individuales. Esto se llama una cascada sigma.
$\sigma_{\theta_{1}\Lambda\theta_{2} }(E)=\sigma_{\theta_{1}}(\sigma_{\theta_{2}}(E))$

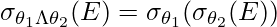
Explicación: La aplicación de $\theta_{1}$ la intersección de condiciones $\theta_{2}$ es costosa. En su lugar, filtre las tuplas que cumplan la condición $\theta_{2}$ (selección interna) y luego aplique la condición $\theta_{1}$ (selección externa) a las tuplas resultantes. Esto nos deja con menos tuplas para procesar la segunda vez. Esto se puede extender para dos o más selecciones que se cruzan. Dado que estamos dividiendo una sola condición en una serie de selecciones o cascadas, se denomina «cascada».
La selección es conmutativa.
$\sigma_{\theta_{1}}(\sigma_{\theta_{2}}(E))=\sigma_{\theta_{2}}(\sigma_{\theta_{1}}(E))$
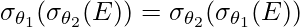
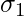Explicación: $\sigma$ la condición es de naturaleza conmutativa. Esto significa que no importa si aplicamos $\sigma_{1}$ primero o 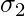$\sigma_{2}$ primero. En la práctica, es mejor y más óptimo aplicar primero la selección que produce un número menor de tuplas. Esto ahorra tiempo en nuestra selección exterior.
Se pueden omitir todas las siguientes proyecciones, solo se requiere la primera proyección. Esto se llama cascada pi.
$\pi_{L_{1}}(\pi_{L_{2}}(...(\pi_{L_{n}}(E))...)) = \pi_{L_{1}}(E)$
Explicación: Una cascada o una serie de proyecciones no tiene sentido. Esto se debe a que, al final, solo estamos seleccionando aquellas columnas que se especifican en la última proyección o la más externa. Por lo tanto, es mejor colapsar todas las proyecciones en una sola, es decir, la proyección más externa.
Las selecciones en productos cartesianos se pueden reescribir como uniones theta.
- Equivalencia 1
  $\sigma_{\theta}(E_{1} \times E_{2}) = E_{1} \bowtie_{\theta} E_{2}$
  Explicación: Se sabe que la operación de productos cruzados es muy costosa. Esto se debe a que empareja cada tupla de E1 (total de m tuplas) con cada tupla de E2 (total de n tuplas). Esto produce m*n entradas. Si aplicamos una operación de selección después de eso, tendríamos que escanear a través de m*n entradas para encontrar las tuplas adecuadas que satisfagan la condición 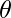$\theta$ . En lugar de hacer todo esto, es más óptimo usar Theta Join, una combinación diseñada específicamente para seleccionar solo aquellas entradas en el producto cruzado que satisfacen la condición Theta, sin evaluar primero todo el producto cruzado.
- Equivalencia 2
  $\sigma_{\theta_{1}}(E_{1} \bowtie_{\theta_{2}} E_{2}) = E_{1} \bowtie_{\theta_{1} \Lambda \theta_{2}} E_{2}$
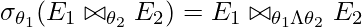
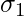  Explicación: Theta Join reduce radicalmente el número de tuplas resultantes, por lo que si aplicamos una intersección de ambas condiciones de unión, es decir, $\theta_{1}$ y $\theta_{2}$ en Theta Join, tenemos menos escaneos que hacer. Por otro lado, una $\sigma_{1}$ condición externa aumenta innecesariamente las tuplas a escanear.
Las uniones theta son conmutativas.
$E_{1} \bowtie_{\theta} E_{2} = E_{2} \bowtie_{\theta} E_{1}$
Explicación: Las uniones theta son conmutativas, y el tiempo de procesamiento de la consulta depende en cierta medida de qué tabla se usa como bucle externo y cuál se usa como bucle interno durante el proceso de unión (según las estructuras de indexación y los bloques).
Las operaciones de unión son asociativas.
- Unión natural
  $(E_{1} \bowtie E_{2}) \bowtie E_{3} = E_{1} \bowtie (E_{2} \bowtie E_{3})$
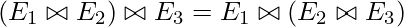
  Explicación: las uniones son todas conmutativas y asociativas, por lo que primero se deben unir las dos tablas que producen menos entradas y luego aplicar la otra unión.
- Unión theta
  $(E_{1} \bowtie_{\theta_{1}} E_{2}) \bowtie_{\theta_{2} \Lambda \theta_{3}} E_{3} = E_{1} \bowtie_{\theta_{1} \Lambda \theta_{3}} (E_{2} \bowtie_{\theta_{2}} E_{3})$
  Explicación: Theta Joins son asociativos de la manera anterior, donde $\theta_{2}$ involucran atributos solo de E2 y E3.
La operación de selección se puede distribuir.
- Equivalencia 1
  $\sigma_{\theta_{1}\Lambda\theta_{2}}(E_{1}\bowtie_{\theta}E_{2})=(\sigma_{\theta_{1}}(E_{1}))\bowtie_{\theta}(\sigma_{\theta_{2}}(E_{2}))$
  Explicación: Aplicar una selección después de realizar Theta Join hace que todas las tuplas devueltas por Theta Join se supervisen después de la unión. Si esta selección contiene atributos de solo E1, es mejor aplicar esta selección a E1 (lo que da como resultado una menor cantidad de tuplas) y luego unirla con E2.
- Equivalencia 2
  $\sigma_{\theta_{0}}(E_{1}\bowtie_{\theta}E_{2})=(\sigma_{\theta_{0}}(E_{1}))\bowtie_{\theta}E_{2}$
  Explicación: Esto se puede extender a dos condiciones de selección, $\theta_{1}$ y $\theta_{2}$ , donde Theta1 contiene los atributos de solo E1 y $\theta_{2}$ contiene atributos de solo E2. Por lo tanto, podemos aplicar individualmente los criterios de selección antes de unir, para reducir drásticamente el número de tuplas unidas.
La proyección se distribuye sobre Theta Join.
- Equivalencia 1
  $\pi_{L_{1}\cup L_{2}}(E_{1}\bowtie_{\theta}E_{2})=(\pi_{L_{1}}(E_{1}))\bowtie_{\theta}(\pi_{L_{2}}(E_{2}))$
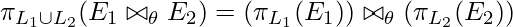
  Explicación: La idea discutida para la selección también se puede usar para la proyección. Aquí, si L1 es una proyección que involucra columnas de solo E1 y L2 otra proyección que involucra columnas de solo E2, entonces es mejor aplicar individualmente las proyecciones en ambas tablas antes de unirlas. Esto nos deja con un número menor de columnas a cada lado, lo que contribuye a una unión más fácil.
- Equivalencia 2
  $\pi_{L_{1}\cup L_{2}}(E_{1}\bowtie_{\theta}E_{2})=\pi_{L_{1}\cup L_{2}}((\pi_{L_{1}\cup L_{3}}(E_{1}))\bowtie_{\theta}(\pi_{L_{2}\cup L_{3}}(E_{2})))$
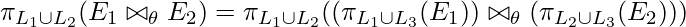
  Explicación: Aquí, al aplicar las proyecciones L1 y L2 en la unión, donde L1 contiene columnas de solo E1 y L2 contiene columnas de solo E2, podemos introducir otra columna E3 (que es común entre ambas tablas). Luego, podemos aplicar las proyecciones L1 y L2 en E1 y E2 respectivamente, junto con la columna añadida L3. L3 nos permite hacer la unión.
La unión y la intersección son conmutativas.
$E_{1}\ \cup E_{2}\ =\ E_{2}\ \cup\ E_{1}$
$E_{1}\ \cap E_{2}\ =\ E_{2}\ \cap\ E_{1}$
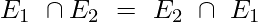
Explicación: La unión y la intersección son ambas distributivas; podemos encerrar cualquier tabla entre paréntesis según los requisitos y la facilidad de acceso.
Unión e Intersección son asociativas.
$(E_{1}\ \cup E_{2})\ \cup\ E_{3}=E_{1}\ \cup\ (E_{2}\ \cup\ E_{3})$
$(E_{1}\ \cap E_{2})\ \cap\ E_{3}=E_{1}\ \cap\ (E_{2}\ \cap\ E_{3})$
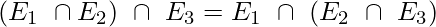
Explicación: La unión y la intersección son ambas distributivas; podemos encerrar cualquier tabla entre paréntesis según los requisitos y la facilidad de acceso.
La operación de selección se distribuye sobre las operaciones de unión, intersección y diferencia.
$\sigma_{P}(E_{1}\ -\ E_{2})=\sigma_{P}(E_{1})\ -\ \sigma_{P}(E_{2})$
Explicación: En diferencia de conjuntos, sabemos que solo se muestran aquellas tuplas que pertenecen a la tabla E1 y no pertenecen a la tabla E2. Por lo tanto, aplicar una condición de selección en toda la diferencia de conjuntos es equivalente a aplicar la condición de selección en las tablas individuales y luego aplicar la diferencia de conjuntos. Esto reducirá el número de comparaciones en el paso de diferencia establecida.
La operación de proyección se distribuye sobre la operación de unión.
$\pi_{L}(E_{1}\ \cup\ E_{2})=(\pi_{L}(E_{1}))\ \cup\ (\pi_{L}(E_{2}))$
Explicación: aplicar proyecciones individuales antes de calcular la unión de E1 y E2 es más óptimo que la expresión de la izquierda, es decir, aplicar la proyección después del paso de unión.

Minimalidad:
se dice que un conjunto de reglas de equivalencia es mínimo si ninguna regla puede derivarse de ninguna combinación de las demás. Se dice que una consulta es óptima cuando es mínima.

Ejemplos:
suponga las siguientes tablas:

instructor(ID, name, dept_name, salary)
teaches(ID, course_id, sec_id, semester, year)
course(course_id, title, dept_name, credits)

Consulta 1: Encuentre los nombres de todos los instructores en el departamento de Música, junto con los títulos de los cursos que imparten

$\pi_{name, title}(\sigma_{dept\_name=``Music"}(instructor \bowtie (teaches \bowtie \pi_{course\_id, title}(course))))$

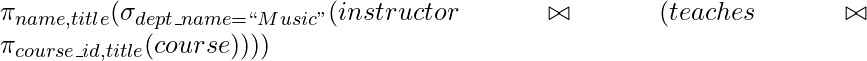
Aquí, dept_name es un campo de solo la tabla de instructores. Por lo tanto, podemos seleccionar a los profesores de música antes de unirse a las mesas, lo que reduce el tiempo de consulta.

Consulta optimizada:
Usar la regla 7a y realizar la selección lo antes posible reduce el tamaño de la relación a unir.
$\pi_{name, title}((\sigma_{dept\_name=``Music"(instructor)}\bowtie(teaches\bowtie\pi_{course\_id, title}(course)))$

Consulta 2: busque los nombres de todos los instructores del departamento de CSE que hayan impartido un curso en 2009, junto con los títulos de los cursos que impartieron

$\sigma_{dept\_name=``CSE"}(\sigma_{year=2009}(instructor\bowtie teaches))$

Consulta optimizada:
podemos realizar una «selección temprana», por lo que la consulta optimizada se convierte en:
$\sigma_{dept\_name=``CSE"}(instructor)\bowtie \sigma_{year=2009}(teaches)$

Este artículo es una contribución de Anannya Uberoi . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta