Clasificación de cálculo de direcciones mediante hash

En este algoritmo de clasificación, la función hash f se usa con la propiedad de la función de conservación del orden , que establece que si $x <= y, f(x) <= f(y)$ .

Función hash:

f(x) = floor( (x/maximum) * SIZE )
where maximum => maximum value in the array,
      SIZE => size of the address table (10 in our case),
      floor => floor function

Este algoritmo utiliza una tabla de direcciones para almacenar los valores, que es simplemente una lista (o array) de listas vinculadas. La función Hash se aplica a cada valor de la array para encontrar su dirección correspondiente en la tabla de direcciones. Luego, los valores se insertan en sus direcciones correspondientes de manera ordenada comparándolos con los valores que ya están presentes en esa dirección.

Ejemplos:

Input : arr = [29, 23, 14, 5, 15, 10, 3, 18, 1] 
Output:
After inserting all the values in the address table, the address table looks like this:

ADDRESS 0: 1 --> 3 
ADDRESS 1: 5 
ADDRESS 2: 
ADDRESS 3: 10 
ADDRESS 4: 14 --> 15 
ADDRESS 5: 18 
ADDRESS 6: 
ADDRESS 7: 23 
ADDRESS 8: 
ADDRESS 9: 29

La siguiente figura muestra la representación de la tabla de direcciones para el ejemplo discutido anteriormente:

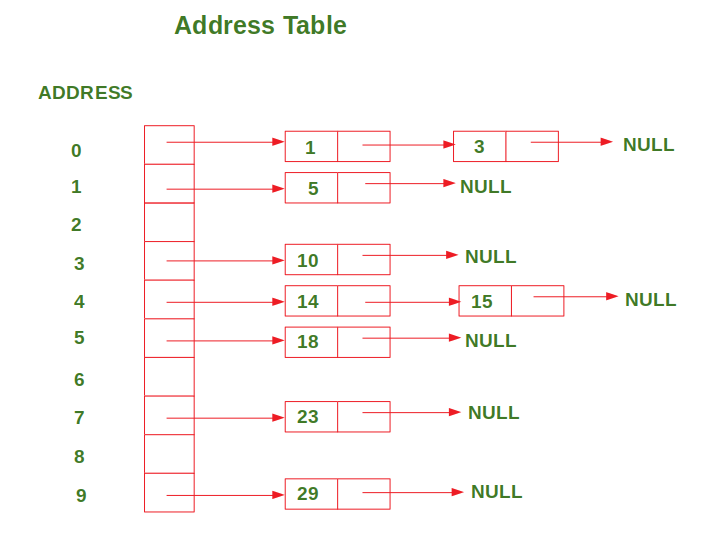
Después de la inserción, se ordenan los valores de cada dirección en la tabla de direcciones. Por lo tanto, iteramos a través de cada dirección una por una e insertamos los valores en esa dirección en la array de entrada.

A continuación se muestra la implementación del enfoque anterior.

# Python3 code for implementation of 
# Address Calculation Sorting using Hashing
  
# Size of the address table (In this case 0-9)
SIZE = 10
  
class Node(object):
  
    def __init__(self, data = None):
        self.data = data
        self.nextNode = None
  
class LinkedList(object):
  
    def __init__(self):
        self.head = None
  
    # Insert values in such a way that the list remains sorted
    def insert(self, data):
        newNode = Node(data)
  
        # If there is no node or new Node's value
        # is smaller than the first value in the list,
  
        # Insert new Node in the first place
        if self.head == None or data < self.head.data:
            newNode.nextNode = self.head
            self.head = newNode
  
        else:
            current = self.head
              
            # If the next node is null or its value
            # is greater than the new Node's value,
   
            # Insert new Node in that place
            while current.nextNode != None \
                    and \
                    current.nextNode.data < data:
                current = current.nextNode
  
            newNode.nextNode = current.nextNode
            current.nextNode = newNode
              
# This function sorts the given list 
# using Address Calculation Sorting using Hashing
def addressCalculationSort(arr):
  
    # Declare a list of Linked Lists of given SIZE
    listOfLinkedLists = []
    for i in range(SIZE):
        listOfLinkedLists.append(LinkedList())
  
    # Calculate maximum value in the array
    maximum = max(arr)
  
    # Find the address of each value
    # in the address table 
    # and insert it in that list
    for val in arr:
        address = hashFunction(val, maximum)
        listOfLinkedLists[address].insert(val)
      
    # Print the address table 
    # after all the values have been inserted
    for i in range(SIZE):
        current = listOfLinkedLists[i].head
        print("ADDRESS " + str(i), end = ": ")
  
        while current != None:
            print(current.data, end = " ")
            current = current.nextNode
  
        print()
      
    # Assign the sorted values to the input array
    index = 0
    for i in range(SIZE):
        current = listOfLinkedLists[i].head
  
        while current != None:
            arr[index] = current.data
            index += 1
            current = current.nextNode
              
  
# This function returns the corresponding address
# of given value in the address table
def hashFunction(num, maximum):
  
    # Scale the value such that address is between 0 to 9
    address = int((num * 1.0 / maximum) * (SIZE-1))
    return address
  
# -------------------------------------------------------
# Driver code
  
# giving the input address as follows
arr = [29, 23, 14, 5, 15, 10, 3, 18, 1]
  
# Printing the Input array
print("\nInput array: " + " ".join([str(x) for x in arr]))
  
# Performing address calculation sort
addressCalculationSort(arr)
  
# printing the result sorted array
print("\nSorted array: " + " ".join([str(x) for x in arr]))

Producción:

Input array: 29 23 14 5 15 10 3 18 1

ADDRESS 0: 1 3 
ADDRESS 1: 5 
ADDRESS 2: 
ADDRESS 3: 10 
ADDRESS 4: 14 15 
ADDRESS 5: 18 
ADDRESS 6: 
ADDRESS 7: 23 
ADDRESS 8: 
ADDRESS 9: 29 

Sorted array: 1 3 5 10 14 15 18 23 29

Complejidad de tiempo:
La complejidad de tiempo de este algoritmo es $O(n)$ en el mejor de los casos. Esto sucede cuando los valores de la array se distribuyen uniformemente dentro de un rango específico.

Mientras que la complejidad del tiempo en el peor de los casos es $O(n^2)$ . Esto sucede cuando la mayoría de los valores ocupan 1 o 2 direcciones porque entonces se requiere mucho trabajo para insertar cada valor en su lugar adecuado.

Publicación traducida automáticamente

Artículo escrito por rituraj_jain y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta